Файл: Учебное пособие предисловие данное учебное пособие предназначено для студентов немате.docx

Данное учебное пособие предназначено для студентов немате- матических факультетов, изучение математики на которых про- исходит в сокращенном объеме. Рассматривается тема «Двой- ные и тройные интегралы» курсов «Математический анализ» или

«Высшая математика». Также дано понятие n-кратного интеграла. Необходимые для решения задач теоретические сведения приводят- ся в каждом разделе.

Пособие содержит подробные решения типовых (и не только) примеров и задач, в конце некоторых разделов дополнительно ука- заны номера примеров из задачника Г. Н. Бермана [4] для самостоя- тельной работы. В самом конце учебного пособия приведено 26 ва- риантов контрольных заданий. Задания составлены с расчетом на индивидуальную работу в пределах группы 25–30 человек.

Материалы пособия в течение нескольких лет использовались при изучении курса «Высшая математика» для направления «Хи- мия» химического факультета СПбГУ.

Настоящее пособие может быть полезно студентам, изучающим указанные курсы или соответствующие темы в других курсах, а также преподавателям.

ДВОЙНОЙ ИНТЕГРАЛ

Некоторые задачи, приводящие к понятию двойного интеграла

Прежде всего решим задачуомассеплоскойфигуры.

∈
Пусть на плоскости Oxyимеется фигура (S) (рис. 1). Пусть в каждой точке M (x, y) (S) задана поверхностная плотность рас- пределения массы μ= f(x,y). Разобьем (S) на nчастей (ΔS_j)

(рис. 2). Обозначим: d_j= sup

^P,Q^∈^(Δ^Sj⁾

{|PQ|} — диаметр части (ΔS_j),

j
λ= max{d_j} — ранг разбиения, ΔS_j— площадь части (ΔS_j).

Рис.1 Рис.2
В каждой частичной области (ΔS_j) возьмем произвольную точ-

ку M_j(x_j,y_j). Приближенное значение массы Δm_jчасти (ΔS_j) вы- ражается равенством Δm_j^∼= f(x_j,y_j)ΔS_j, а вся масса фигуры (S)

n n

j=1

j=1

m= ^ΣΔm_j^∼= ^Σf(x_j,y_j)ΔS_j.

Последнее равенство тем точнее, чем меньше ранг разбиения λ.

Будем разбивать (S) на все более мелкие части так, чтобы

λ_n−_→→_∞0. Для каждого разбиения будем выбирать точки M_jи со-

Σ
ставлять суммы n

j=1
f(x_j,y_j)ΔS_j

. Точное значение массы будет вы-

ражаться формулой

m= lim

λ→0
n

Σ
f(x_j,y_j)ΔS_j. (1)

j=1

Аналогично рассматривается задача о величине электрическогоили магнитного заряда плоской пластины (S), если поверхност- ная плотность распределения заряда равна f (x, y). Решение также имеет вид (1).

Точно такое же решение будет в задаче об объеме цилиндрическо-го бруса. Имеется пространственная область, ограниченная снизу плоскостью Oxy, с боков — цилиндрической поверхностью, прохо- дящей через границу фигуры (S), лежащей в плоскости Oxy, с об- разующими, параллельными оси Oz, сверху — поверхностью с урав- нением z = f (x, y) (рис. 3, a). Эту пространственную область обыч- но называют цилиндрическимбрусом. Требуется найти его объем.

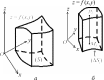
Рис.3
Разобьем, как и ранее, основание (S) на n частей (ΔS_j), через границу каждой части проведем цилиндрическую поверхность с об- разующими, параллельными оси Oz. Тогда цилиндрический брус разобьется на n столбиков (рис. 3, б ). В основании (ΔS_j) j-го стол- бика, j = 1, 2,... , n, возьмем произвольную точку M_j(x_j, y_j) и вы- числим f (x_j, y_j). Заменим рассматриваемый столбик цилиндром с тем же основанием (ΔS_j), образующими, параллельными оси Oz, и высотой h_j= f (x_j, y_j). Его объем Δv_jбудет равен h_jΔS_j. Поэтому объем Δv_jизображенной на рис. 3, бчасти цилиндрического бруса

дается приближенным равенством Δv_j^∼= h_jΔS_j.

Объем всего цилиндрического бруса находится по формуле
n n

j=1

j=1

V= ^ΣΔv_j^∼= ^Σf(x_j,y_j)ΔS_j.

Последнее равенство тем точнее, чем меньше ранг разбиения. По- этому

Σ
n

V= lim f(x_j,y_j)ΔS_j. (2)

λ→0 _j₌₁

Существует много других задач, решения которых имеют такой же вид.

1 2 3 4 5 6 7 8 9 ... 17

Определение двойного интеграла

∈
Пусть на плоскости Oxy имеется фигура (S) (см. рис. 1). Пусть в каждой точке M (x, y) (S) задана функция f (x, y). Разобьем, как и выше, (S) на nчастей (ΔS_j) (см. рис. 2). Обозначим: d_j— диа- метр частичной области (ΔS_j), λ — ранг разбиения, ΔS_j— площадь части (ΔS_j). В каждой части (ΔS_j) возьмем произвольную точку

M_j(x_j,y_j) и составим сумму

f(x_j,y_j)ΔS_j. Эта сумма называет-
_Σn

j=1

ся интегральнойсуммой, соответствующей взятому разбиению и

выбору точек M_j.

→∞
Продолжим разбиение фигуры (S) так, чтобы λ−→ 0. При каж-

дом разбиении будем выбирать точки M

n

_jв каждой частичной об-

ласти и составлять соответствующие интегральные суммы. Предел последовательности интегральных сумм называется двойным ин-тегралом от функции f по области (S), если этот предел не зависит ни от способа разбиения, ни от выбора точек M_j:

∫∫ f(x,y) dxdy

Σ

n
def

= lim
f(x_j,y_j)ΔS_j. (3)

(S)

λ→0 _j₌₁

∫∫
Множество (S) называется областьюинтегрирования, f — подынтегральной функцией, x, y — переменными интегрирования. Если существует f(x,y) dxdy, то функция fназывается инте-

(S)

грируемойпообласти(S).

Основные классы интегрируемых функций. Основные свойства двойного интеграла

Основные классы интегрируемых функций

Приведем без доказательств две теоремы о достаточных усло- виях интегрируемости функции¹.

Теорема 1. Функция, непрерывная на замкнутом множестве

, интегрируема по этому множеству.

Теорема 2. Функция, ограниченная и непрерывная на замкну- том множестве (S), исключая конечное множество точек и линий²разрыва, интегрируема по этому множеству.