ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 19.03.2024
Просмотров: 186
Скачиваний: 0
СОДЕРЖАНИЕ
№1 дәріс. Телекоммуникациялық жүйелерді модельдеудің мақсаттары мен мәселелері
Үлестірудің берілген заңымен кездейсоқ сандарды модельдеу
Cтандартты сандық атрибуттер (ССА).
Бір арналы құрылғының атрибуттері.
Көпканалды құрылғыларды моделдеу
STORAGE аты1, С1/аты2, С2…/атыn, Cn
Транзакттардың параметрлерін басқару.
Буль операторлары OR (немесе) және AND (және).
№6 дәріс. Функциялар және кестелер.
№7 дәріс. Оқиғалар ағындарының модельдері. Марков үрдісі. Күтуді қамтитын ЖҚЖ.
Оқиғалар ағындарының модельдері
Қызмет көрсету үрдісін Марковтық кездейсоқ үрдіс ретінде қарастыру
№8 дәріс. Колмогоровтың теңдеулері. Жойылу және таралу сұлбасы
Колмогоров теңдеулерін құрудың жалпы ережелері.
№9 дәріс. Жаппай қызмет ету жүйелерінің әр түрлерінің сипаттамаларын есептеу
Бірканалды шығындармен жұмыс істейтін ЖҚЖ.
Шектеулі кезекті бірканалдық ЖҚКЖ
№10 дәріс. Тұйық және күту уақыты шектелген жаппай қызмет көрсету жүйелері
Ps
s! P0 ,
. . . .
n
Pn 1,
ескере отырып
Pn s! sns
P0 ,
где n s.
P0

1
s1 n
1
n
s1 n s .

ns
n0 n!
-
n!sns
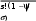 n0 n!
n0 n!Жүйенің негізгі сипаттамаларын келесі түрде анықтаймыз
Pотк 0, q 1 Pотк 1.
Абсолюттік өткізу қабілеті
A q =
осыдан, бос емес каналдардың орта саны
Кезектегі тапсырыстардың орта саны
n s1
(n s) Pn
n s1
(n s)
n
s!sn s
P0 ,
Түрлендірілгеннен кейін
s1
P.
(s 1)! (s )2 0
Жүйедегі тапсырыстардың жалпы саны
Жүйеде болу уақытының орта мәні
-
z.
u (s 1)! (s )2 P0 1.
Көрсетілген формулардың барлығы тек қана стационарлы режим үшін орынды. Кезегі шектелмеген көпканалды жүйе стационарлы режимде жұмыс
істеу үшін келесі шарт орындалуы тиіс
s
1.
- 1 ... 17 18 19 20 21 22 23 24 ... 27
№10 дәріс. Тұйық және күту уақыты шектелген жаппай қызмет көрсету жүйелері
Дәрістің мақсаты: тұйық және күту уақыты шектелген жаппай қызмет көрсету жүйелерінің сипаттамаларын есептеу әдістерін оқып білу.
Мазмұны
а) тұйық ЖҚЖ:
ә) күту уақыты шектелген ЖҚЖ.
Тұйық ЖҚЖ
 Тапсырыстардың саны жүйенің қызмет көрсетуімен шектелген жағдайды қарастырайық. Мысалы, mбірлік құрылғылардың sжөндеу бригадаларымен қайта қалпына келтіру процесі. Әрбір құрылғы орташа tраб , уақыт жұмыс істеп, одан кейін бұзылады. Әрбір құрылғының істен шығу
Тапсырыстардың саны жүйенің қызмет көрсетуімен шектелген жағдайды қарастырайық. Мысалы, mбірлік құрылғылардың sжөндеу бригадаларымен қайта қалпына келтіру процесі. Әрбір құрылғы орташа tраб , уақыт жұмыс істеп, одан кейін бұзылады. Әрбір құрылғының істен шығуекпінділігі
1 tраб
( құрылғының жұмыс істеу уақыты көрсеткіштік заңымен
таралған деп есептейміз). Жөндеуден кейін құрылғы жүйенің кірісіне
екпінділікпен қайта қосылады (кайтадан істен шығуы мүмкін).
Егер белгілі бір уақыт аралығында nқұрылғы жөнделіп немесе жөндеуді
күтіп отырса, ал m-nжұмыс істеп жатса, онда t, t dt аралығында істен шығу
ықтималдылығы
ndt (m n) dt
тең - жүйеге тапсырыстардың келу
екпінділігі жүйеге келіп түскен тапсырыстардың санына байланысты.
Бір қызмет көрсету каналы және m тапсырыстары бар тұйық ЖҚЖ үшін ауысулар графын тұрғызайық.
m (m-1) (m-2)
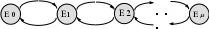
1.11 Сурет. Ауысулар графы.
Азаю және көбею сұлбаларын қолданып, күй ықтималдылық теңдеуін құрайық
P m P,
1 0
P2
m(m 1)2
2 P0
Pn
m(m 1)...(m n 1)n
n P0
немесе Pm! nP,
n
P0
(m n)! 0
1 .

(m n)!
mm! n
n0
Берілген жүйе үшін абсолютті өткізу қабілеті А– ақаулардың орташа саны, қызмет көрсету каналымен уақыт бірлігінде түзелетін және
A Pзан ,
мұндағы Pзан — каналдың бос болмау ықтималдылығы, немесе
z Pзан 1 P0 ;
Pсвоб P0 ;
(1 P0 ).
Істен шыққан қондырғылардың орташа саны
m
n0
жұмыс күйінде болады,
(m
ақаулар ағыны. Барлық ақаулар
(1 P0 )
қызмет
көрсету каналымен түзеледі. Сонда
(m
0
Кезектегі тапсырыстардың орташа саны
0
m (1 P) (1 1 ).
0
Тұйық жүйелерде тапсырыстар саны әрқашан шектеулі және қызмет көрсету каналының екпінділігіне байланыссыз қалыптасқан режим болады.
k
m
каналдың бос болмау коэффициенті бірге жақын болғанда, «шоғырлану»
құбылысы туады.
Бұл жағдайда тапсырыстардың барынша көбі жинақтаушы мен ЖҚЖ-ң қызмет көрсету каналында жинақталып, тапсырыстардың аз мөлшері жүйеден тыс болады.
S қызмет көрсету каналы бар тұйық ЖҚЖ-ны қарастырайық. Ауысулар графы
 m (m 1) (m 2)
m (m 1) (m 2)(m s) (m s 1)
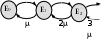 … s
… sS
s1 …
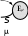 S S
S S1.12- Сурет. Ауысулар графы.
Күй ықтималдылық теңдеуі
P1 m P0 ,
P m(m1)P,
2 2! 0

