Файл: Курсовой проект по дисциплине Железобетонные и каменные конструкции.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 11.04.2024
Просмотров: 174
Скачиваний: 0
СОДЕРЖАНИЕ
1 Расчет монолитного ребристого перекрытия с балочными плитами
1.2 Расчет монолитной плиты перекрытия
1.2.1 Вычисление расчетных пролетов и нагрузок на плиту
1.2.2 Характеристика прочности бетона
1.2.3 Подбор сечений продольной арматуры сеток
1.3 Расчет и проектирование второстепенной монолитной балки
1.3.1 Сбор нагрузок и определение усилий во второстепенной балке
1.3.2 Характеристики прочности бетона и арматуры
1.3.3 Расчет прочности второстепенной балки по сечениям, нормальным к продольной оси
1.3.4 Расчет сечения второстепенной балки по наклонным сечениям
2 Расчет балочного сборного перекрытия
2.1 Компоновка конструктивной схемы балочного сборного перекрытия
2.2 Расчет полки ребристой плиты перекрытия
2.3 Расчет поперечных ребер плиты
2.6 Потери предварительного напряжения арматуры
2.7 Проверка образования трещин
2.8 Расчет по раскрытию трещин.
3.1 Задание геометрических размеров и сбор нагрузок на ригель
3.2 Расчет ригеля на прочность по нормальному сечению
3.4 Построение эпюры материалов
4 Расчет центрально сжатой колонны
5 Расчет центрально нагруженного фундамента под колонну
6 Расчет кирпичного столба с сетчатым армированием
7 Расчет ребристой плиты по СП
7.1 Расчет ребристой плиты по предельным состояниям I группы
7.2 Расчет поперечных ребер плиты
7.3 Расчет продольного ребра плиты
7.4 Расчет ребристой плиты по предельным состояниям II группы
7.5 Потери предварительного напряжения арматуры
7.6 Проверка образования трещин
7.7 Расчет по раскрытию трещин, нормальных к продольной оси плиты
7.4 Расчет ребристой плиты по предельным состояниям II группы
Согласно табл. 2 /1/ ребристая плита, эксплуатируемая в закрытом помещении и армированная напрягаемой арматурой класса A 600 должна удовлетворять 3-й категории требований по трещиностойкости, т.е. допускается непродолжительное раскрытие трещин шириной 0,4 мм и продолжительное – 0,3 мм. Прогиб плиты от действия постоянных и длительных нагрузок не должен превышать предельного значения – 3 см по табл.4 /1/.
Определение геометрических характеристик приведенного сечения плиты
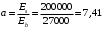
– площадь приведенного сечения:
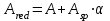

– Статический момент площади приведенного сечения относительно нижней грани:
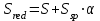
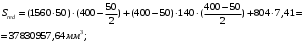
– расстояние от нижней грани до центра тяжести приведенного сечения:
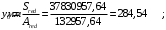
– момент инерции приведенного сечения:
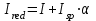
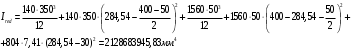
– момент сопротивления приведенного сечения по нижней зоне:
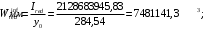
– момент сопротивления приведенного сечения по верхней зоне:
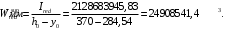
7.5 Потери предварительного напряжения арматуры
Определяем первые потери предварительного напряжения арматуры по позициям 1-6 таблицы 5 /1/. Арматура стержневая A600, способ натяжения электротермический.
– потери от релаксации напряжений в арматуре:
Ϭ1 = 0,03∙ Ϭsp = 0,03∙ 540= 16,2 МПа;
– потери от температурного перепада:
Ϭ2 = 1,25
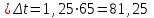 МПа;
МПа;– потери от деформации стальной формы:
σ3 = 0 МПа.
– потери от деформации анкеров:
σ4 = 0 МПа.
Таким образом, усилие обжатия PI с учетом потерь 1-4 равно:
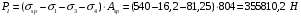
Точка приложения усилия PI совпадает с центром тяжести сечения напрягаемой арматуры, поэтому еор = у0 – а = 284,54 – 30 = 254,54 мм.
Для определения потерь от быстронатекающей ползучести бетона вычисляем напряжение в бетоне в середине пролета от действия силы PI и изгибающего момента Mw от собственной массы плиты:
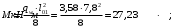
- напряжение на уровне растянутой арматуры (т. е. при у = е0 = =254,54мм);
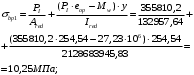
Назначаю передаточную прочность бетона Rbp = 13,5 МПа. Согласно /10/ (п. 2.2.3.10) Предварительные напряжения в бетоне σbpпри передаче усилия предварительного обжатия Р(1), определяемого с учетом первых потерь, не должны превышать: если напряжения уменьшаются или не изменяются при действии внешних нагрузок - 0,9Rbp
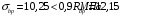 ,
,Условие выполняется.
Первые потери составляют:
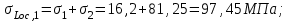
Вторые потери предварительного напряжения арматуры;
- потери от усадки бетона:
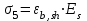
где: εb,sh– деформации усадки бетона, значения которых можно приближенно принимать в зависимости от класса бетона равными:
0,0002- для бетона классов В35 и ниже;
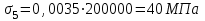
- потери от ползучести бетона:
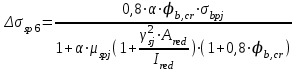
где φb,cr - коэффициент ползучести бетона, определяемый согласно п. 2.1.2.7;
σbpj - напряжения в бетоне на уровне центра тяжести рассматриваемой j-й группы стержней напрягаемой арматуры;
ysj – расстояние между центрами тяжести сечения рассматриваемой группы стержней напрягаемой арматуры и приведенного поперечного сечения элемента;
Ared, Ired– площадь приведенного сечения элемента и ее момент инерции относительно центра тяжести приведенного сечения;
μspj– коэффициент армирования, равный Aspj /А, где А
и Aspj – площади поперечного сечения соответственно элемента и рассматриваемой группы стержней напрягаемой арматуры.
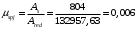
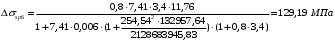
Вторые потери составляют:
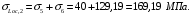
Суммарные потери составляют:
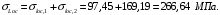
Усилие обжатия с учетом суммарных потерь составит:
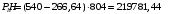
7.6 Проверка образования трещин
Расчет предварительно напряженных изгибаемых элементов по раскрытию трещин производят в тех случаях, когда соблюдается условие
М > Мcrc
где: М - изгибающий момент от внешней нагрузки;
Мcrc - изгибающий момент, воспринимаемый нормальным сечением элемента при образовании трещин, определяемый согласно п. 4.2.2.
Момент образования трещин предварительно напряженных изгибаемых элементов без учета неупругих деформаций растянутого бетона определяют, как для сплошного упругого тела по формуле:
Mcrc = Rbt,ser W + P eяр,
где: eяр = е0р+ r - расстояние от точки приложения усилия предварительного обжатия Р до ядровой точки, наиболее удаленной от растянутой зоны, трещинообразование которой проверяется;
е0р - то же, до центра тяжести приведенного сечения;
r - расстояние от центра тяжести приведенного сечения до ядровой точки, определяемое по формуле:
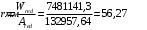 ,
,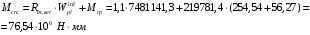
Так как Mcrc = 76,54 кН∙м < Mн = 99,12 кН∙м трещины в растянутой зоне образуются необходим расчет по раскрытию трещин.
7.7 Расчет по раскрытию трещин, нормальных к продольной оси плиты
Ширину раскрытия нормальных трещин определяют по формуле:
где: σs - напряжение в продольной растянутой арматуре в нормальном сечении с трещиной от соответствующей внешней нагрузки, определяемое согласно п. 4.2.3.2;
ls - базовое (без учета влияния вида поверхности арматуры) расстояние между смежными нормальными трещинами;
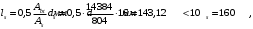
следовательно, принимаем
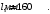
ψs - коэффициент, учитывающий неравномерное распределение относительных деформаций растянутой арматуры между трещинами (ψs = 1);
φ1 - коэффициент, учитывающий продолжительность действия нагрузки, принимаемый равным:
1,0- при непродолжительном действии нагрузки;
1,4- при продолжительном действии нагрузки;
φ2 - коэффициент, учитывающий профиль продольной арматуры, принимаемый равным:
0,5- для арматуры периодического профиля и канатной;
0,8- для гладкой арматуры (класса А240);
φ3 - коэффициент, учитывающий характер нагружения, принимаемый равным:
1,0- для изгибаемых и внецентренно сжатых элементов;
1,2- для растянутых элементов.
Значения напряжений σsв растянутой арматуре изгибаемых предварительно напряженных элементов от внешней нагрузки определяют по формуле:
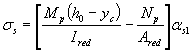
где: Ired, Ared, yc - момент инерции, площадь приведенного поперечного сечения элемента и расстояние от наиболее сжатого волокна до центра тяжести приведенного сечения, определяемые с учетом площади сечения только сжатой зоны бетона, площадей сечения растянутой и сжатой арматуры согласно п. 4.3.3.5;
αs1=
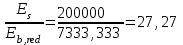
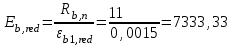
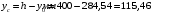
Np – усилие предварительного обжатия;
Мp – изгибающий момент от внешней нагрузки и усилия предварительного обжатия, определяемый по формуле:
Mp = M ± Npe0p
Для Мtot = 99,12 кН∙м значение Мрдля полной нагрузки равняется:
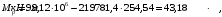
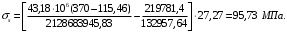
Для Мl = 78,84 кН∙м значение Мрдля полной нагрузки равняется:
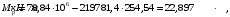
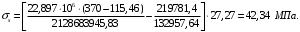
Ширина раскрытия трещин от продолжительного действия постоянных и временных длительных нагрузок равняется:
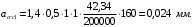
Ширина раскрытия трещин от непродолжительного действия постоянных и временных (длительных и кратковременных) нагрузок:
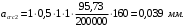
Ширина раскрытия трещин от непродолжительного действия постоянных и временных длительных нагрузок равняется:
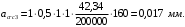
Ширина продолжительного раскрытия трещин:
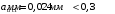
Ширина непродолжительного раскрытия трещин:
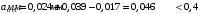
Требования к плите по трещиностойкости удовлетворяются.
7.8 Расчёт плиты по деформациям
Полная кривизна для участка с трещинами в растянутой зоне определяется по формуле:
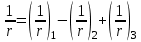 где:
где: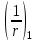 – кривизна от непродолжительного действия всей нагрузки;
– кривизна от непродолжительного действия всей нагрузки;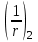 – кривизна от непродолжительного действия постоянных и длительных нагрузок;
– кривизна от непродолжительного действия постоянных и длительных нагрузок; 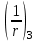 – кривизна от продолжительного действия постоянных и длительных нагрузок.
– кривизна от продолжительного действия постоянных и длительных нагрузок.На участках, где в растянутой зоне образуются нормальные к продольной оси элемента трещины, кривизна изгибаемых элементов определяется по формуле:
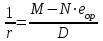
где: M – момент относительно оси, нормальной к плоскости действия момента и проходящий через центр тяжести площади сечения арматуры, от всех внешних сил, расположенных по одну сторону от рассматриваемого сечения, и от усилия предварительного обжатия;
Npи е0p – усилие предварительного обжатия и его эксцентриситет относительно центра тяжести приведенного поперечного сечения элемента$
D - изгибная жесткость приведенного поперечного сечения элемента, определяемая по формуле:
D = Eb1 / Ired,
где: Еb1 – модуль деформации сжатого бетона

