Файл: Курсовой проект по дисциплине Железобетонные и каменные конструкции.docx

, то расчет производится как для прямоугольного сечения шириной b = bf = 800 мм.
Определяем коэффициент статического момента α_m



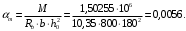
по приложению 4/2/нахожу η=0,995.
Класс арматуры А400, R_s=355МПа для Ø 6-8 мм.





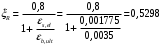
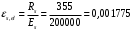
по /10/ определяем ξ=0,016< ξR=0,5298; η=0,995;

Из сортамента стержневой и проволочной арматуры принимаю 1 стержень Ø 6 мм, арматура А400, с площадью рабочей арматуры A_s=28,3 мм².
Расчет поперечного ребра плиты на действие поперечной силы.

По /9/ из условия свариваемости принимаем поперечные стержни диаметром 3 мм класса В 500 с числом каркасов – 1 с шагом поперечных стержней s = 100 мм.

А_sw = 7,1 мм²

R_sw = 300 МПа,

R_bt = 0,9∙0,9=0,81 МПа

Е_s = 200000МПа

Е_b = 27000МПа

Проверяем условие:

,

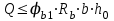где φ_b1 =0,3 (/9/ п.6.2.34);

тогда:



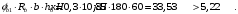
Условие выполняется, прочность по наклонной полосе между трещинами обеспечена.

Проверяем условие:

;

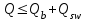где Q_b - поперечное усилие, воспринимаемое бетоном:



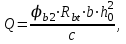
где: φ_b2 = 1,5;

с - длина проекции наиболее опасного наклонного сечения на продольную ось элемента, равная 3h₀.



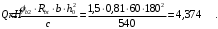
Q_sw - поперечная сила, воспринимаемая поперечной арматурой в наклонном сечении. Поперечную силу Q_sw определяют по формуле:



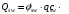
где: φ_sw=0,75 (/9/ п.6.2.34);

с - длина проекции наиболее опасной наклонной трещины на продольную ось элемента равная 2h₀;

q_sw - усилие в поперечной арматуре на единицу длины элемента, определяемое по формуле:



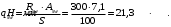
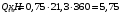
Проверяем условие:

---

;

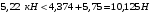Условие выполняется, следовательно, прочность наклонного сечения обеспечена.

---

7.3 Расчет продольного ребра плиты

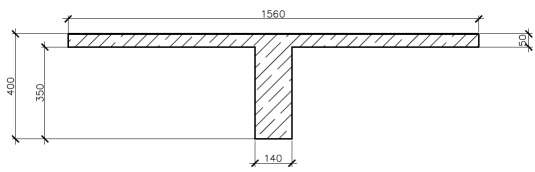
Рисунок 11 – Поперечное сечение продольного ребра
Таблица 9 – Нагрузки на 1 м ребристой плиты

Вид нагрузки	qн, кН/м	γf	qр, кН/м
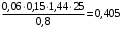
Постоянная: от массы полки плиты: 0,05∙1,56∙25=1,95 от массы поперечных ребер: собственная масса продольного ребра: 0,14∙0,35∙25=1,225 от массы пола:0,5∙1,56=0,78	1,95 0,405 1,225 0,78	1,1 1,1 1,1 1,3	2,145 0,4455 1,3475 1,014
Итого	4,36		4,952
Временная длительная: 4,2∙1,56=6,552 кратковременная: 1,8∙1,56=2,808	6,552 2,808	1,2 1,2	7,8624 3,3696
Итого	9,36		11,232
Всего	13,72		16,184

С учетом коэффициента надежности по классу ответственности здания:

Для расчетов по I группе предельных состояний:

;

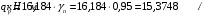Для расчета по II группе предельных состояний:

• 
  полная:
  

;

• 
  длительная:
  

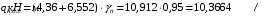
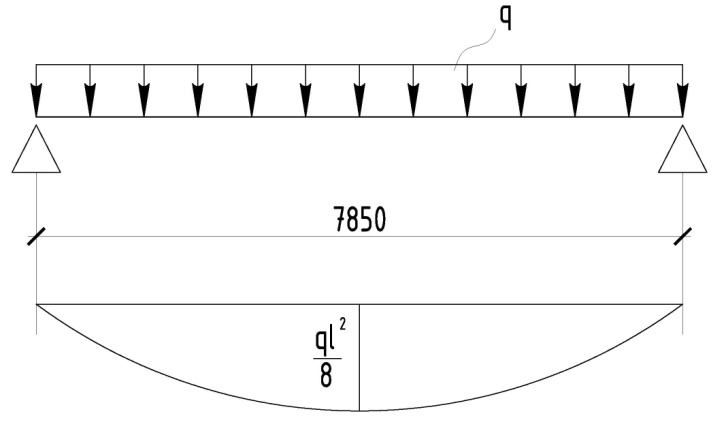
Рисунок 12 – Расчетная схема продольного ребра
h₀=400-30=370мм.

Класс предварительно напрягаемой арматуры А 600

R­_s=520 МПа

R_{s ser}=590 МПа
Расчетные усилия:

Для расчетов по I группе предельных состояний:





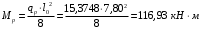
Для расчетов по II группе предельных состояний:

---

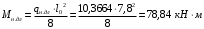
Величина предварительного напряжения в соответствии с /9/ ( п.2.2.3.1) назначается равным

σ_sp = 0,9∙ R_s,n = 0,9∙600 = 540 МПа.


Определяем положение нейтральной оси





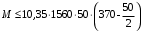
116,93·10⁶ Н·мм < 278,52·10⁶ Н·мм

Так как условие выполняется, то граница сжатой зоны проходит в полке, и расчет производим как для прямоугольного сечения шириной
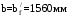
Определяем коэффициент статического момента α_m





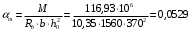
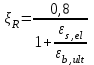
где 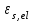для напрягаемой арматуры определяется по формуле: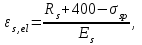



где: σ_sp - предварительное напряжение в арматуре с учетом всех потерь и γ_sp = 0,9.

Так как согласно /9/ в общем случае суммарные потери должны быть не менее 100 МПа и 30% от величины предварительного напряжения, то σ_sp определяется по формуле






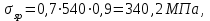
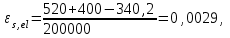
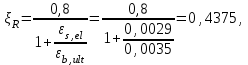
Проверяем условие: ξ = 0,054< ξ_R = 0,4375; η = 0,973. Условие выполняется.

Определяем коэффициент, учитывающий предварительное напряжение арматуры


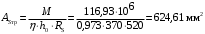
Принимаем 4 стержня Ø16 А 600, Аs= 804 мм².

Расчёт прочности сечений, наклонных к продольной оси.
Из условия свариваемости принимаем поперечные стержни диаметром 8 мм класса А400 с числом каркасов – 2 с шагом поперечных стержней s=150 мм.

А_sw = 2х50,3=100,6 мм²

R_sw = 285 МПа,

R_bt = 0,9∙0,9=0,81 МПа

Е_s = 200000МПа

Е_b = 27000МПа

Проверяем условие:

,

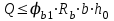где φ_b1 =0,3 (/9/ п.6.2.34);

тогда:

---

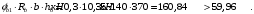
Условие выполняется, прочность по наклонной полосе между трещинами обеспечена.

Проверяем условие:

;

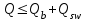где Q_b - поперечное усилие, воспринимаемое бетоном:



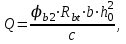
где: φ_b2 = 1,5;

с - длина проекции наиболее опасного наклонного сечения на продольную ось элемента, равная 3h₀.



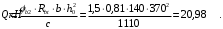
Q_sw - поперечная сила, воспринимаемая поперечной арматурой в наклонном сечении. Поперечную силу Q_sw определяют по формуле:



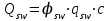
где: φ_sw=0,75 (/9/ п.6.2.34);

с - длина проекции наиболее опасной наклонной трещины на продольную ось элемента равная 2h₀;

q_sw - усилие в поперечной арматуре на единицу длины элемента, определяемое по формуле:



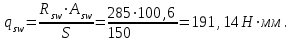
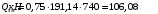
Проверяем условие:

;

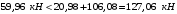Условие выполняется, следовательно, прочность наклонного сечения обеспечена.

---