Файл: Курсовой проект по дисциплине Железобетонные и каменные конструкции.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 11.04.2024
Просмотров: 177
Скачиваний: 0
СОДЕРЖАНИЕ
1 Расчет монолитного ребристого перекрытия с балочными плитами
1.2 Расчет монолитной плиты перекрытия
1.2.1 Вычисление расчетных пролетов и нагрузок на плиту
1.2.2 Характеристика прочности бетона
1.2.3 Подбор сечений продольной арматуры сеток
1.3 Расчет и проектирование второстепенной монолитной балки
1.3.1 Сбор нагрузок и определение усилий во второстепенной балке
1.3.2 Характеристики прочности бетона и арматуры
1.3.3 Расчет прочности второстепенной балки по сечениям, нормальным к продольной оси
1.3.4 Расчет сечения второстепенной балки по наклонным сечениям
2 Расчет балочного сборного перекрытия
2.1 Компоновка конструктивной схемы балочного сборного перекрытия
2.2 Расчет полки ребристой плиты перекрытия
2.3 Расчет поперечных ребер плиты
2.6 Потери предварительного напряжения арматуры
2.7 Проверка образования трещин
2.8 Расчет по раскрытию трещин.
3.1 Задание геометрических размеров и сбор нагрузок на ригель
3.2 Расчет ригеля на прочность по нормальному сечению
3.4 Построение эпюры материалов
4 Расчет центрально сжатой колонны
5 Расчет центрально нагруженного фундамента под колонну
6 Расчет кирпичного столба с сетчатым армированием
7 Расчет ребристой плиты по СП
7.1 Расчет ребристой плиты по предельным состояниям I группы
7.2 Расчет поперечных ребер плиты
7.3 Расчет продольного ребра плиты
7.4 Расчет ребристой плиты по предельным состояниям II группы
7.5 Потери предварительного напряжения арматуры
7.6 Проверка образования трещин
7.7 Расчет по раскрытию трещин, нормальных к продольной оси плиты
Ширину раскрытия трещин от непродолжительного действия полной нагрузки определяем по формуле
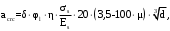
где δ – коэффициент, принимаемый для изгибаемых элементов
равным 1;
φl – коэффициент, принимаемый равным 1;
η – коэффициент, принимаемый при стержневой арматуре периодического профиля равным 1;
σ – напряжение в стержнях крайнего ряда арматуры или приращение напряжений от действия внешней нагрузки;
μ – коэффициент армирования сечения;
d – диаметр арматуры.
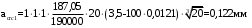
Ширина раскрытия трещин от непродолжительного действия постоянной и длительной нагрузки
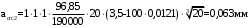
Ширина раскрытия трещин от продолжительного действия постоянной и длительной нагрузки
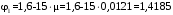
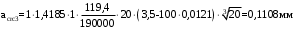
Ширина непродолжительного раскрытия трещин:
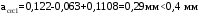
Ширина продолжительного раскрытия трещин:
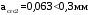
Требования к плите по трещиностойкости удовлетворяются.
2.9 Расчет прогиба плиты
Расчет выполняется с учетом раскрытия трещин согласно п. 4.27 /1/ от действия постоянной и длительной нагрузок.
M = Mн = 99,12 кН∙м; Nн = PII = 159,37 кН
На участках, где в растянутой зоне образуются нормальные к продольной оси элемента трещины, кривизна изгибаемых элементов определяется по формуле
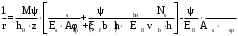
где M – момент относительно оси, нормальной к плоскости действия момента и проходящий через центр тяжести площади сечения арматуры, от всех внешних сил, расположенных по одну сторону от рассматриваемого сечения, и от усилия предварительного обжатия;
z – расстояние от центра тяжести площади сечения арматуры до точки приложения равнодействующих усилий в сжатой зоне сечения над трещиной;
ψs – коэффициент, учитывающий работу растянутого бетона на участке с трещинами;
ψb – коэффициент, учитывающий неравномерность распределения деформаций крайнего сжатого волокна бетона по длине участка с трещинами;
φf – 1,37;
ξ – относительная высота сжатой зоны бетона;
ν – коэффициент, характеризующий упругопластическое состояние бетона сжатой зоны;
Nн – равнодействующая продольной силы и усилия предварительного обжатия.
Полная кривизна для участка с трещинами в растянутой зоне определяется по формуле
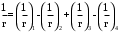 где:
где: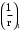 – кривизна от непродолжительного действия всей нагрузки;
– кривизна от непродолжительного действия всей нагрузки;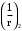 – кривизна от непродолжительного действия постоянных и длительных нагрузок;
– кривизна от непродолжительного действия постоянных и длительных нагрузок; 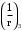 – кривизна от продолжительного действия постоянных и длительных нагрузок;
– кривизна от продолжительного действия постоянных и длительных нагрузок; 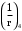 – кривизна, обусловленная выгибом элемента вследствие усадки и ползучести бетона от усилия предварительного обжатия
– кривизна, обусловленная выгибом элемента вследствие усадки и ползучести бетона от усилия предварительного обжатияКривизна от непродолжительного действия всей нагрузки:
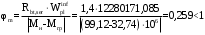
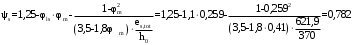
при
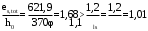
принимаем
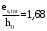
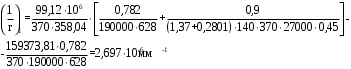
Кривизна от непродолжительного действия постоянных и длительных
нагрузок:
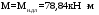
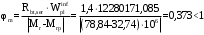
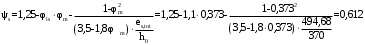 при
при 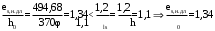
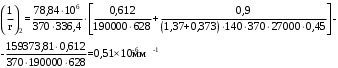
Кривизна от продолжительного действия постоянных и длительных нагрузок:
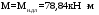
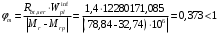
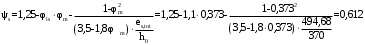 при
при 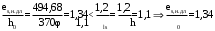
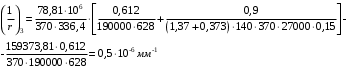
Кривизна, обусловленная выгибом элемента вследствие усадки и ползучести бетона от усилия предварительного обжатия:
Определяем относительные деформации бетона, вызванные его усадкой и ползучестью от усилия предварительного обжатия:
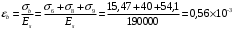
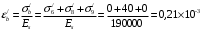
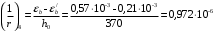
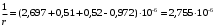
Вычисляем прогиб по формуле
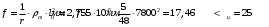
Вычисленное значение прогиба удовлетворяет требованиям.
3 Расчет разрезного ригеля
3.1 Задание геометрических размеров и сбор нагрузок на ригель
Назначаем предварительно следующие значения геометрических размеров ригеля, высота и ширина поперечного сечения:
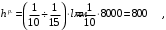
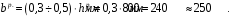
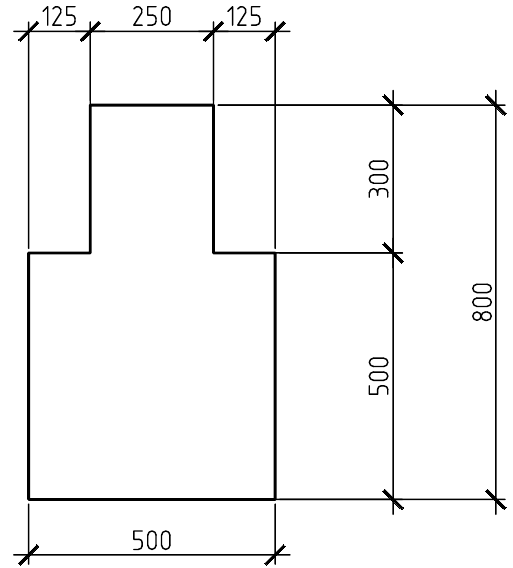
Рисунок 13 – Расчетное сечение ригеля
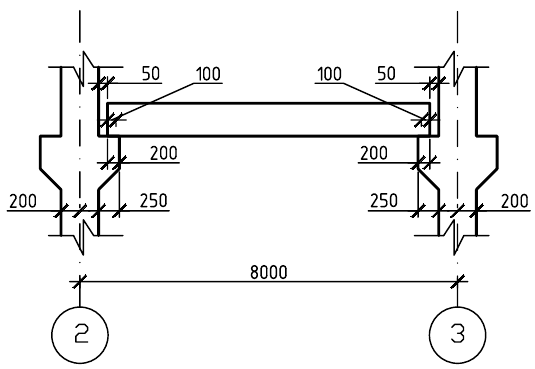
Рисунок 14 – Определение расчетного пролета ригеля
Расчетный пролет ригеля равен
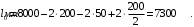
Сбор нагрузки на 1 м длины ригеля. Нагрузка на ригеле от ребристых плит считается равномерно распределенной. Ширина грузовой полосы на ригель равна шагу колонн здания 8 м. Подсчет приведен в таблице 5.
Таблица 10 – Сбор нагрузок на разрезной ригель
| Наименование нагрузки | qn,кПа | 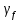 | q,кПа |
| Постоянная: - от собственного веса ригеля 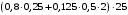 - от массы пола 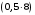 - от собственного веса плиты 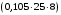 | 8,125 4 21 | 1,1 1,3 1,1 | 8,9375 5,2 23,1 |
| Итого: | 33,125 | | 37,2375 |
| Полезная нагрузка на перекрытие 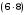 | 48 | 1,2 | 57,6 |
| Всего: | 81,125 | | 94,84 |
3.2 Расчет ригеля на прочность по нормальному сечению
Бетон тяжелый, класса В25 естественного твердения. Прочность при осевом сжатии Rb=11,5 МПа, прочность при осевом растяжении Rbt=0,9 МПа, модуль упругости Еb= 30·103 МПа. Для арматуры класса А-III R
s=365 МПа. Коэффициент условий работы бетонаγb2=0,9, учитывая его в расчетах, получим
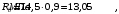
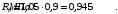
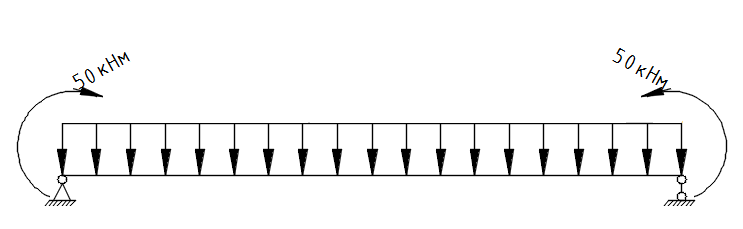
Рисунок 15 – Расчетная схема ригеля
Расчет ригеля на середине опоры
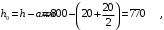
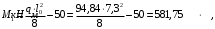
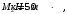
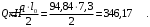
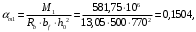
.
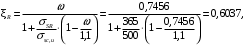
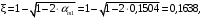
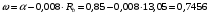
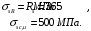
Условие
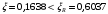 выполняется, установка сжатой арматуры не требуется.
выполняется, установка сжатой арматуры не требуется.По таблице 3.1 /Байков, Сигалов/ нахожу η=0,9218.
Определим требуемую площадь сечения арматуры АSтр
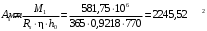 .
.Принимаю 4 стержней ⌀28мм с площадью рабочей арматуры AS=2463 мм2. Шаг стержней сетки в поперечном направлении 200 мм.
Расчет ригеля на опоре
Для сечения должно выполняться условие
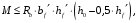
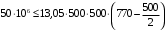
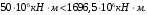

.
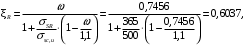
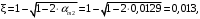
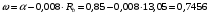
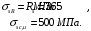
Условие
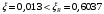 выполняется, установка сжатой арматуры не требуется.
выполняется, установка сжатой арматуры не требуется.По таблице 3.1 /Байков, Сигалов/ нахожу η=0,9935.
Определим требуемую площадь сечения арматуры АSтр
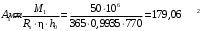
Принимаю 2 стержней ⌀12мм с площадью рабочей арматуры AS

