Добавлен: 12.04.2024
Просмотров: 89
Скачиваний: 0
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
СОДЕРЖАНИЕ
3.1.2. Абсолютно неупругий удар
Удар материальной точки о неподвижную поверхность
Прямой удар материальной точки о неподвижную поверхность
Косой удар материальной точки о неподвижную поверхность
Теорема о движении центра масс системы материальных точек при ударе
Прямой центральный удар двух абсолютно твердых тел
Рассмотрим атт массы м, закрепленное в точке о подпятником, а в точке в – подшипником (рис. 4).
Учитывая, что в данном случае, а, из формулы [6]
Условия отсутствия ударных реактивных импульсов атт, вращающегося относительно неподвижной оси
(24)
Так как в рассматриваемом случае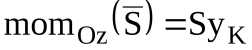
, где
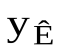– кратчайшее расстояние линии действия ударного импульса 
от оси вращения z, то шестое соотношение формулы (22) примет вид [6]:
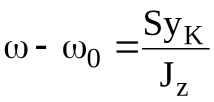. (25)
Из уравнений (24) и (25) найдем после исключения разности
следующее соотношение [6]:
(26)
Таким образом, уравнение (24) будет иметь место при любой численной величине ударного импульса , если линия действия этого импульса будет проходить через точку К, которая отстоит от оси вращения z на расстоянии yК, определяемом формулой (26).
Условиями отсутствия ударных реактивных импульсов АТТ, вращающегося вокруг неподвижной оси, являются:
-ударный импульс должен быть перпендикулярен плоскости, проходящей через ось вращения z и центр масс АТТ;
-ударный импульс должен быть расположен в плоскости, перпендикулярной оси z и проходящей через точку О1 АТТ, для которой ось z является главной осью инерции;
-точка приложения К ударного импульса должна находиться от оси z на расстоянии, определяемом формулой (26) (точку К, через которую при этом проходит линия действия ударного импульса, не вызывающего ударных реакций в точках закрепления оси, называют центром удара).
В частном случае, если центр масс АТТ находится на оси вращения, то есть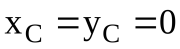
, то из формулы (26) следует
. То есть в этом случае нельзя добиться отсутствия ударных реактивных импульсов. Так как дополнительные динамические реакции АТТ, вращающегося вокруг неподвижной оси, могут отсутствовать только в случае, если ось вращения является центральной (
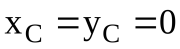), то добиться одновременно отсутствия дополнительных динамических реакций и ударных реактивных импульсов АТТ, вращающегося вокруг неподвижной оси при ударе, невозможно.
3.3. Методы анализа удара материальных систем
Дискретные модели.
Метод конечных элементов
Решения задач о коллинеарном ударе двух твердых тел на основе гипотезы Ньютона (комплементарный подход) и методами волновой теории могут рассматриваться как полярные и в смысле сложности вычислений, и в смысле соответствия результатов реальности. С практической точки зрения каждая из таких моделей обладает весьма существенными недостатками: первая слишком груба и не позволяет определить важные характеристики процесса удара, как его длительность максимальную нагрузку и т.п. Вторая модель в этом смысле более привлекательна, однако уравнения волновой теории, как правило, очень сложны для решения, поэтому в ее рамках остается открытым основной вопрос определения ударного импульса как функции начальных условий.
Переход от непрерывной модели описания деформируемого твердого тела к представлению его при помощи конечного числа связанных между собой подчастей носит название метода конечных элементов. В общем случае анализ дискретной многомерной системы требует использования численных методов исследования. Эти методы могут оказаться неэффективными при расчете моделей быстро повторяющихся (множественных) ударов. При рассмотрении дискретных систем используются два метода, известные в литературе под названиями: комплементарный подход и метод функции штрафов (в порядке исторического появления) [1, 5].
Комплементарный подход
Комплементарный подход к задачам ударной механики восходит к Ньютону, который ввел в постановку задачи закон восстановления. При комплементарном подходе длительность удара полагается равной нулю. Одновременно с этим считается, что координаты системы являются непрерывными функциями времени, а скорости могут испытывать в точках ударов конечные скачки.
Метод функции штрафа в ударной механике
Метод функции штрафа обосновывает комплементарный подход и является аналогом идеи введения сильного потенциального поля при описании
гамильтоповой системы с голономными связями, развитой Арнольдом. Для исследования уравнений движения тел в фазе удара в уравнения движения вводится параметризованная сила, в виде градиента потенциала U, которая отвечает за проникновение тела вглубь препятствия. Длительность фазы удара полагается ненулевой [4].
Численный анализ и моделирование
Метод функции штрафов является по своей сути процедурой, через которую выводятся законы восстановления, вводящиеся априори или при помощи эксперимента, как при комлементарпом подходе. Однако, при расчете численных схем взаимодействия объектов в реальном времени возникает проблема, состоящая в том, что решения уравнений движения, параметризованных жесткостью, при разных значения параметра и мелкости разбиения схем численных алгоритмов, дают разные результаты. Так как реальные физические системы обладают, быть может, большой, но конечной жесткостью, то мелкость разбиения должна быть связана с жесткостью, чтобы приводить к единственным и корректным результатам.
Биллиарды.Устойчивость и хаос в динамических системах
Движение материальной точки в замкнутой ограниченной области пространства называется биллиардом, если при ударах о границу препятствия не происходит потерь энергии и угол падения равен углу отражения. Биллиарды, будучи чрезвычайно простыми по своей сути, демонстрируют всю сложность нелинейной динамики. В конце 18 века Э.Ф. Хладни положил начало экспериментам, которые предвосхитили все последующие работы, связанные с биллиардами. Хладни заметил, что если металлическую пластину заставить вибрировать с помощью скрипичного смычка, то мелкие песчинки, случайно рассыпанные по ее поверхности, самоорганизуются в геометрические фигуры (фигуры Хладни). Эти фигуры, в тех областях, где они появляются, характеризуют систему как устойчивую по отношению к изменению начальных данных.
Метод пространственно-временных преобразований для описания динамики систем с ударами как развитие метода пенальтизации
В системах с ударами фазовые траектории являются разрывными функциями времени. Поскольку траектории систем разрывны, то их невозможно описывать обыкновенными дифференциальными уравнениями и поэтому естественно использовать более общий тип динамических уравнений, а именно: нелинейные дифференциальные уравнения с мерами. Эти уравнения являются универсальным средством строгого описания динамики дискретно-непрерывной системы (далее – ДНС) [5, 8]. Однако управление такими системами в фазе удара представляет собой значительно более сложную задачу, чем управление чисто дискретными или непрерывными системами. В последние годы в задачах оптимального управления ДНС была предложена и детально разработана новая методология, применимая для широкого класса задач оптимального управления с различными типами ограничений.
Основой нового подхода является метод разрывной замены времени или, более обще, метод пространственно-временных сингулярных преобразований.
Описание явления удара (т.е. резкого изменения скоростей) в терминах некоторого быстрого движения похоже на введение в систему импульсного управления. Тогда подобное пространственно-временное преобразование можно рассматривать, как некоторую модификацию метода разрывной замены времени [4]. Такой подход позволяет корректно описать результат единичного соударения. Однако исследование ситуации с бесконечным числом соударений, возникновением точек накопления моментов соударений и «слипания» тел вызывает серьезные трудности [3]. Изучение подобных систем имеет большое значение вследствие развития в последнее время робототехники, точной механики и управления движением.
Если рассматривать фазу удара, как управляемый процесс, то можно пойти еще дальше. Управление в фазе удара подразумевает воздействия, которые происходят в темпе контакта, то есть достаточно быстро. Один из наиболее ярких примеров такого рода можно наблюдать при игре в настольный теннис, когда опытный игрок успевает за время контакта мяча с поверхностью ракетки быстро развернуть ее, придав мячу дополнительное, очень сильно вращение (этот удар называется топ-спин). Другой пример, это селективный захват или, наоборот, отталкивание металлического предмета, например, с помощью электромагнита. Ясно, что электромагнит нужно включать, создавая либо силу притяжения, либо отталкивания только тогда, когда предмет касается его поверхности. В такой постановке задачи управления в механических системах с односторонними ограничениями похожи па задачи импульсного управления.
4. Заключение. Практическое применение теории удара
В целом, теория удара отражает общий уровень развития теоретической и прикладной физике, отвечая на конъюнктурный спрос в сведения, позволяющих оптимизировать производственный процессы и конечные изделия, позволяя сделать более безопасными, экономичными их производство и эксплуатацию.
Основные современные направления применения теории удара:
- в квантовой физике для изучения их строения и свойств элементарных частиц в результате ударного взаимодействия атомов и субатомных элементов в разного рода ускорителях частиц.
- в машиностроении и металлообработке при обработке металлических изделий с помощью удара.
- для расчета ударного взаимодействия спускаемых аппаратов различными средами при спуске и посадке в условиях Земли и тел Солнечной системы.
- в проектировании транспортных средств, бытовой техники, оружия, робототехники и т.п. для расчета запаса прочности конструкции.
- в медицине и биотехнике для расчета прочности конструкции материалов для протезирования.
- в материаловедении для расчета прочностных характеристик получаемых конструкционных материалов.
- для обеспечения экологической и промышленной безопасности при эксплуатации различных видов техники.
- для обеспечения безопасности эксплуатации транспортных средств.
- для расчета различных видов гидроударов.
5. Список использованных источников:
Так как в рассматриваемом случае
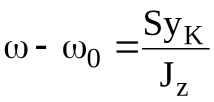, где – кратчайшее расстояние линии действия ударного импульса от оси вращения z, то шестое соотношение формулы (22) примет вид [6]: . (25)Из уравнений (24) и (25) найдем после исключения разности
следующее соотношение [6]: (26)Таким образом, уравнение (24) будет иметь место при любой численной величине ударного импульса
, если линия действия этого импульса будет проходить через точку К, которая отстоит от оси вращения z на расстоянии yК, определяемом формулой (26).Условиями отсутствия ударных реактивных импульсов АТТ, вращающегося вокруг неподвижной оси, являются:
-ударный импульс должен быть перпендикулярен плоскости, проходящей через ось вращения z и центр масс АТТ;
-ударный импульс должен быть расположен в плоскости, перпендикулярной оси z и проходящей через точку О1 АТТ, для которой ось z является главной осью инерции;
-точка приложения К ударного импульса должна находиться от оси z на расстоянии, определяемом формулой (26) (точку К, через которую при этом проходит линия действия ударного импульса, не вызывающего ударных реакций в точках закрепления оси, называют центром удара).
В частном случае, если центр масс АТТ находится на оси вращения, то есть
, то из формулы (26) следует . То есть в этом случае нельзя добиться отсутствия ударных реактивных импульсов. Так как дополнительные динамические реакции АТТ, вращающегося вокруг неподвижной оси, могут отсутствовать только в случае, если ось вращения является центральной (
), то добиться одновременно отсутствия дополнительных динамических реакций и ударных реактивных импульсов АТТ, вращающегося вокруг неподвижной оси при ударе, невозможно.3.3. Методы анализа удара материальных систем
Дискретные модели.
Метод конечных элементов
Решения задач о коллинеарном ударе двух твердых тел на основе гипотезы Ньютона (комплементарный подход) и методами волновой теории могут рассматриваться как полярные и в смысле сложности вычислений, и в смысле соответствия результатов реальности. С практической точки зрения каждая из таких моделей обладает весьма существенными недостатками: первая слишком груба и не позволяет определить важные характеристики процесса удара, как его длительность максимальную нагрузку и т.п. Вторая модель в этом смысле более привлекательна, однако уравнения волновой теории, как правило, очень сложны для решения, поэтому в ее рамках остается открытым основной вопрос определения ударного импульса как функции начальных условий.
Переход от непрерывной модели описания деформируемого твердого тела к представлению его при помощи конечного числа связанных между собой подчастей носит название метода конечных элементов. В общем случае анализ дискретной многомерной системы требует использования численных методов исследования. Эти методы могут оказаться неэффективными при расчете моделей быстро повторяющихся (множественных) ударов. При рассмотрении дискретных систем используются два метода, известные в литературе под названиями: комплементарный подход и метод функции штрафов (в порядке исторического появления) [1, 5].
Комплементарный подход
Комплементарный подход к задачам ударной механики восходит к Ньютону, который ввел в постановку задачи закон восстановления. При комплементарном подходе длительность удара полагается равной нулю. Одновременно с этим считается, что координаты системы являются непрерывными функциями времени, а скорости могут испытывать в точках ударов конечные скачки.
Метод функции штрафа в ударной механике
Метод функции штрафа обосновывает комплементарный подход и является аналогом идеи введения сильного потенциального поля при описании
гамильтоповой системы с голономными связями, развитой Арнольдом. Для исследования уравнений движения тел в фазе удара в уравнения движения вводится параметризованная сила, в виде градиента потенциала U, которая отвечает за проникновение тела вглубь препятствия. Длительность фазы удара полагается ненулевой [4].
Численный анализ и моделирование
Метод функции штрафов является по своей сути процедурой, через которую выводятся законы восстановления, вводящиеся априори или при помощи эксперимента, как при комлементарпом подходе. Однако, при расчете численных схем взаимодействия объектов в реальном времени возникает проблема, состоящая в том, что решения уравнений движения, параметризованных жесткостью, при разных значения параметра и мелкости разбиения схем численных алгоритмов, дают разные результаты. Так как реальные физические системы обладают, быть может, большой, но конечной жесткостью, то мелкость разбиения должна быть связана с жесткостью, чтобы приводить к единственным и корректным результатам.
Биллиарды.Устойчивость и хаос в динамических системах
Движение материальной точки в замкнутой ограниченной области пространства называется биллиардом, если при ударах о границу препятствия не происходит потерь энергии и угол падения равен углу отражения. Биллиарды, будучи чрезвычайно простыми по своей сути, демонстрируют всю сложность нелинейной динамики. В конце 18 века Э.Ф. Хладни положил начало экспериментам, которые предвосхитили все последующие работы, связанные с биллиардами. Хладни заметил, что если металлическую пластину заставить вибрировать с помощью скрипичного смычка, то мелкие песчинки, случайно рассыпанные по ее поверхности, самоорганизуются в геометрические фигуры (фигуры Хладни). Эти фигуры, в тех областях, где они появляются, характеризуют систему как устойчивую по отношению к изменению начальных данных.
Метод пространственно-временных преобразований для описания динамики систем с ударами как развитие метода пенальтизации
В системах с ударами фазовые траектории являются разрывными функциями времени. Поскольку траектории систем разрывны, то их невозможно описывать обыкновенными дифференциальными уравнениями и поэтому естественно использовать более общий тип динамических уравнений, а именно: нелинейные дифференциальные уравнения с мерами. Эти уравнения являются универсальным средством строгого описания динамики дискретно-непрерывной системы (далее – ДНС) [5, 8]. Однако управление такими системами в фазе удара представляет собой значительно более сложную задачу, чем управление чисто дискретными или непрерывными системами. В последние годы в задачах оптимального управления ДНС была предложена и детально разработана новая методология, применимая для широкого класса задач оптимального управления с различными типами ограничений.
Основой нового подхода является метод разрывной замены времени или, более обще, метод пространственно-временных сингулярных преобразований.
Описание явления удара (т.е. резкого изменения скоростей) в терминах некоторого быстрого движения похоже на введение в систему импульсного управления. Тогда подобное пространственно-временное преобразование можно рассматривать, как некоторую модификацию метода разрывной замены времени [4]. Такой подход позволяет корректно описать результат единичного соударения. Однако исследование ситуации с бесконечным числом соударений, возникновением точек накопления моментов соударений и «слипания» тел вызывает серьезные трудности [3]. Изучение подобных систем имеет большое значение вследствие развития в последнее время робототехники, точной механики и управления движением.
Если рассматривать фазу удара, как управляемый процесс, то можно пойти еще дальше. Управление в фазе удара подразумевает воздействия, которые происходят в темпе контакта, то есть достаточно быстро. Один из наиболее ярких примеров такого рода можно наблюдать при игре в настольный теннис, когда опытный игрок успевает за время контакта мяча с поверхностью ракетки быстро развернуть ее, придав мячу дополнительное, очень сильно вращение (этот удар называется топ-спин). Другой пример, это селективный захват или, наоборот, отталкивание металлического предмета, например, с помощью электромагнита. Ясно, что электромагнит нужно включать, создавая либо силу притяжения, либо отталкивания только тогда, когда предмет касается его поверхности. В такой постановке задачи управления в механических системах с односторонними ограничениями похожи па задачи импульсного управления.
4. Заключение. Практическое применение теории удара
В целом, теория удара отражает общий уровень развития теоретической и прикладной физике, отвечая на конъюнктурный спрос в сведения, позволяющих оптимизировать производственный процессы и конечные изделия, позволяя сделать более безопасными, экономичными их производство и эксплуатацию.
Основные современные направления применения теории удара:
- в квантовой физике для изучения их строения и свойств элементарных частиц в результате ударного взаимодействия атомов и субатомных элементов в разного рода ускорителях частиц.
- в машиностроении и металлообработке при обработке металлических изделий с помощью удара.
- для расчета ударного взаимодействия спускаемых аппаратов различными средами при спуске и посадке в условиях Земли и тел Солнечной системы.
- в проектировании транспортных средств, бытовой техники, оружия, робототехники и т.п. для расчета запаса прочности конструкции.
- в медицине и биотехнике для расчета прочности конструкции материалов для протезирования.
- в материаловедении для расчета прочностных характеристик получаемых конструкционных материалов.
- для обеспечения экологической и промышленной безопасности при эксплуатации различных видов техники.
- для обеспечения безопасности эксплуатации транспортных средств.
- для расчета различных видов гидроударов.
5. Список использованных источников:
-
Воронин, В. В. Динамика процесса посадки спускаемого аппарата на участке его контакта с поверхностью // Вестник Самарского государственного аэрокосмического университета. 2012. № 4 (35) / В.В. Воронин. С. 52-58. -
Иванов, А.П., Динамика систем с механическими соударениями, / А.П. Иванов. Москва: Международная программа образования, 1997. 336 с. -
Лейбович, М. В. Теория удара в задачах и примерах : учеб, пособие / М. В. Лейбович. Хабаровск: Изд-во ТГУ, 2016. 236 с. -
Кочетков, А.В., Федотов, П.В. Некоторые вопросы теории удара // Интернет-журнал «Науковедение». 2013. №5 / А.В. Кочетков, П.В. Федотов. Главный редактор К.А. Кирсанов. ИГУПИТ, 2013. электронный ресурс. http://publ.naukovedenie.ru. -
Рабинович, Б.А. Безопасность космонавта при посадочном ударе спускаемого аппарата о грунт / Б.А. Рабинович. М: Книга и бизнес, 2014.
278 с. -
Тарг, С. М. Краткий курс теоретической механики : учеб. для втузов / С.М. Тарг. 10-е изд., перераб. и доп. М.: Высшая школа, 1986. 416 с. -
W. Evans, D. Jonson, M. Walker An Eulerian approach to soil impact analysis for crashworthiness applications // Durban : International Journal of Impact Engineering. 2016. №91. Р. 14-24.