Добавлен: 12.04.2024
Просмотров: 88
Скачиваний: 0
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
СОДЕРЖАНИЕ
3.1.2. Абсолютно неупругий удар
Удар материальной точки о неподвижную поверхность
Прямой удар материальной точки о неподвижную поверхность
Косой удар материальной точки о неподвижную поверхность
Теорема о движении центра масс системы материальных точек при ударе
Прямой центральный удар двух абсолютно твердых тел
Рассмотрим атт массы м, закрепленное в точке о подпятником, а в точке в – подшипником (рис. 4).
Учитывая, что в данном случае, а, из формулы [6]
Условия отсутствия ударных реактивных импульсов атт, вращающегося относительно неподвижной оси
,
откуда на основании равенств (16) находим [6]:
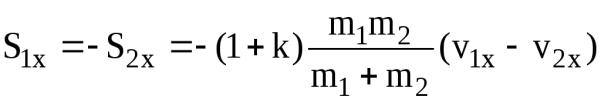 . (17)
. (17)
Все эти уравнения получены в предположении, что поступательное движение АТТ до удара происходит в одном направлении.
Если второе АТТ до удара было неподвижно, то в формулах (16) и (17) следует положить , и тогда получим [6]:
, и тогда получим [6]:
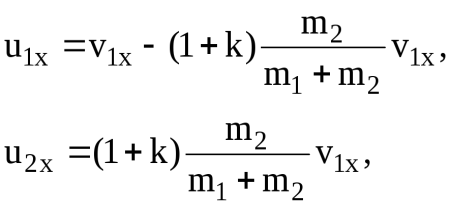
 .
.
Если первое АТТ ударяется о неподвижную преграду (например, о стену), то следует принять в формулах (16) и
и . Поделив числитель и знаменатель соотношений (16) и (17) на
. Поделив числитель и знаменатель соотношений (16) и (17) на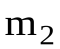 и переходя к пределу при
и переходя к пределу при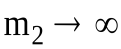 , найдем [6]:
, найдем [6]:
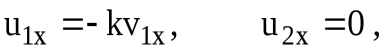
 .
.
Потеря кинетической энергии при прямом центральном ударе двух абсолютно твердых тел.
Теорема Карно
Если удар не вполне упругий, то соударяющиеся АТТ не восстанавливают полностью своей формы в конце удара. Следовательно, часть кинетической энергии, которой обладали эти АТТ в начале удара, тратится на остающуюся деформацию их, а также на нагревание этих АТТ. Подсчитаем величину кинетической энергии, теряемой при прямом центральном ударе двух АТТ, полагая, что удар является не вполне упругим.
Предполагая, что соударяющиеся АТТ движутся поступательно, найдем кинетическую энергию СМТ, состоящую из двух АТТ, в начале и в конце рассматриваемого удара [6]:
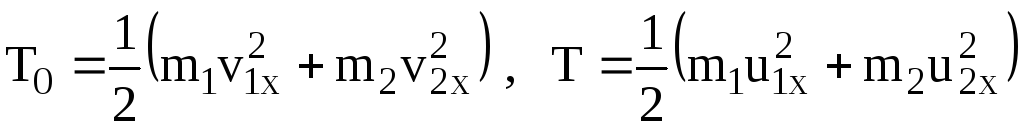 .
.
Следовательно, потеря кинетической энергии при ударе равна [6]:
 . (18)
. (18)
Из уравнения (14) можно получить [6]:
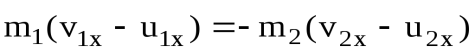 . (19)
. (19)
Подставляя это значение в равенство (18) , получаем [6]:
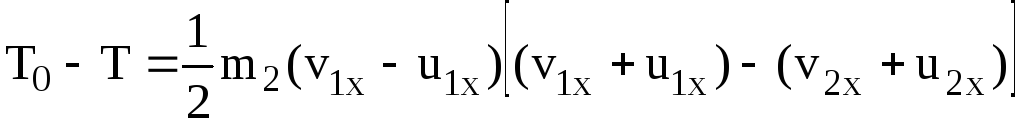 . (20)
. (20)
Но из равенства (15) следует, что [6]
 ,
,
при этом, очевидно, имеет место равенство [6]:
 ,
,
из которого находим [6]:
 .
.
Подставляя это значение в равенство (20), получаем [6]:
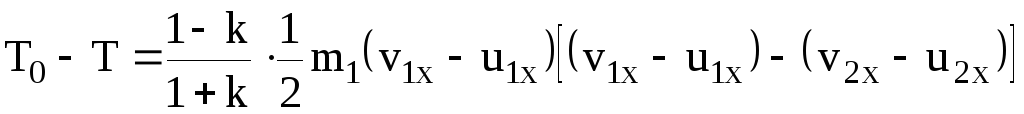 .
.
Используя равенство (19), полученную формулу представим в виде[6]:
 , (21)
, (21)
где разности показывают, насколько уменьшилась при ударе скорость каждого из соударяющихся АТТ, а поэтому их называют потерянными при ударе скоростями.
показывают, насколько уменьшилась при ударе скорость каждого из соударяющихся АТТ, а поэтому их называют потерянными при ударе скоростями.
Равенство (21) составляет содержание теоремы Карно.
Теорема: Кинетическая энергия, потерянная СМТ, при прямом центральном и не вполне упругом ударе двух АТТ, равна - й доле той кинетической энергии, которую имела бы СМТ, если бы ее АТТ двигались с потерянными скоростями.
- й доле той кинетической энергии, которую имела бы СМТ, если бы ее АТТ двигались с потерянными скоростями.
Определение ударных реактивных импульсов АТТ, вращающегося относительно неподвижной оси
Для определения этих пяти неизвестных воспользуемся теоремами о движении центра масс СМТ (11) и об изменении кинетического момента СМТ (13) при ударе в проекциях на оси декартовой системы координат.
Так как АТТ за время удара перемещается бесконечно мало, то векторы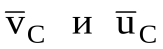 будут параллельны оси Оx и, следовательно,
будут параллельны оси Оx и, следовательно,
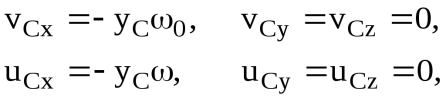
где yC – расстояние центра масс АТТ от оси вращения z , а
0 и – угловые скорости АТТ соответственно до и после удара.

Получим [6]:

Проектируя соотношение [6]

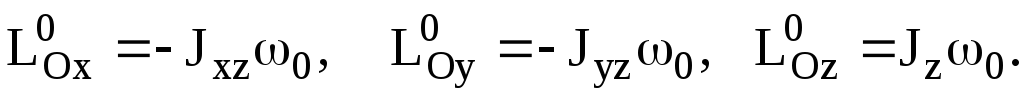
Аналогично для проекций кинетического момента АТТ после удара на оси декартовой системы координат получим [6]:

Подставив все эти значения в уравнения (11) и (13), имеем [6]:
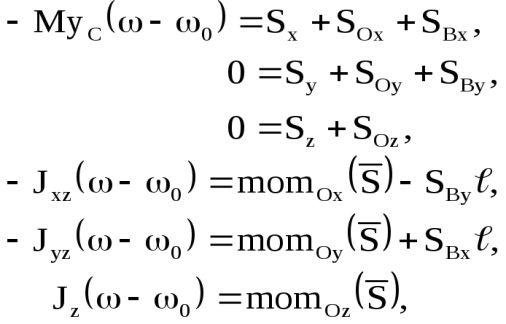 (22)
(22)
где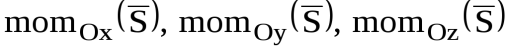 – моменты ударного импульса относительно осей декартовой системы координат.
– моменты ударного импульса относительно осей декартовой системы координат.
Из первых пяти уравнений (22) могут быть найдены пять неизвестных реактивных импульсов ,
, ,
, ,
,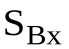 ,
,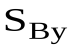 . Из шестого уравнения (22) определяется изменение угловой скорости АТТ ( – 0), вращающегося вокруг неподвижной оси при ударе.
. Из шестого уравнения (22) определяется изменение угловой скорости АТТ ( – 0), вращающегося вокруг неподвижной оси при ударе.
Найдем условия отсутствия ударных реактивных импульсов.
Для этого в первых пяти уравнениях (22) положим их равными нулю. Тогда уравнения (22) примут вид [6]:
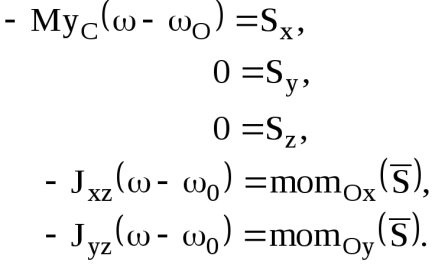 (23)
(23)
Из второго и третьего уравнений (23) следует, что для отсутствия ударных реактивных импульсов необходимо, чтобы приложенный ударный импульс был направлен параллельно оси Оx, то есть перпендикулярно плоскости yОz, которая проходит через ось вращения и центр масс АТТ (рис. 5).
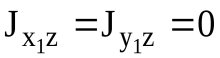 ,
,
то есть ось вращения z для точки О1 должна быть главной осью инерции.
Следовательно, для отсутствия ударных реактивных импульсов необходимо расположить ударный импульс в плоскости x1O1y1, проходящей через точку О1, для которой ось z является главной осью инерции.
в плоскости x1O1y1, проходящей через точку О1, для которой ось z является главной осью инерции.
Первое соотношение (23) примет вид [6]:
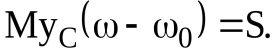
откуда на основании равенств (16) находим [6]:
Все эти уравнения получены в предположении, что поступательное движение АТТ до удара происходит в одном направлении.
Если второе АТТ до удара было неподвижно, то в формулах (16) и (17) следует положить
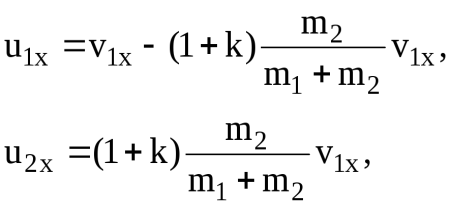
Если первое АТТ ударяется о неподвижную преграду (например, о стену), то следует принять в формулах (16)
Потеря кинетической энергии при прямом центральном ударе двух абсолютно твердых тел.
Теорема Карно
Если удар не вполне упругий, то соударяющиеся АТТ не восстанавливают полностью своей формы в конце удара. Следовательно, часть кинетической энергии, которой обладали эти АТТ в начале удара, тратится на остающуюся деформацию их, а также на нагревание этих АТТ. Подсчитаем величину кинетической энергии, теряемой при прямом центральном ударе двух АТТ, полагая, что удар является не вполне упругим.
Предполагая, что соударяющиеся АТТ движутся поступательно, найдем кинетическую энергию СМТ, состоящую из двух АТТ, в начале и в конце рассматриваемого удара [6]:
Следовательно, потеря кинетической энергии при ударе равна [6]:
Из уравнения (14) можно получить [6]:
Подставляя это значение в равенство (18) , получаем [6]:
Но из равенства (15) следует, что [6]
 ,
,при этом, очевидно, имеет место равенство [6]:
 ,
,из которого находим [6]:
Подставляя это значение в равенство (20), получаем [6]:
Используя равенство (19), полученную формулу представим в виде[6]:
где разности
Равенство (21) составляет содержание теоремы Карно.
Теорема: Кинетическая энергия, потерянная СМТ, при прямом центральном и не вполне упругом ударе двух АТТ, равна
Определение ударных реактивных импульсов АТТ, вращающегося относительно неподвижной оси
Рассмотрим атт массы м, закрепленное в точке о подпятником, а в точке в – подшипником (рис. 4).
 Рис. 4 [6]. | Пусть при этом ОВ= При действии на АТТ ударного импульса |
Для определения этих пяти неизвестных воспользуемся теоремами о движении центра масс СМТ (11) и об изменении кинетического момента СМТ (13) при ударе в проекциях на оси декартовой системы координат.
Так как АТТ за время удара перемещается бесконечно мало, то векторы
где yC – расстояние центра масс АТТ от оси вращения z , а
0 и – угловые скорости АТТ соответственно до и после удара.
Учитывая, что в данном случае, а, из формулы [6]

Получим [6]:

Проектируя соотношение [6]

на оси декартовой системы координат Oxyz, получим проекции кинетического момента атт до удара на эти оси [6]:
Аналогично для проекций кинетического момента АТТ после удара на оси декартовой системы координат получим [6]:
Подставив все эти значения в уравнения (11) и (13), имеем [6]:
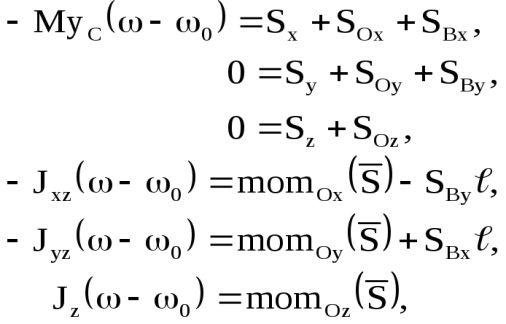 (22)
(22)где
Из первых пяти уравнений (22) могут быть найдены пять неизвестных реактивных импульсов
Условия отсутствия ударных реактивных импульсов атт, вращающегося относительно неподвижной оси
Найдем условия отсутствия ударных реактивных импульсов.
Для этого в первых пяти уравнениях (22) положим их равными нулю. Тогда уравнения (22) примут вид [6]:
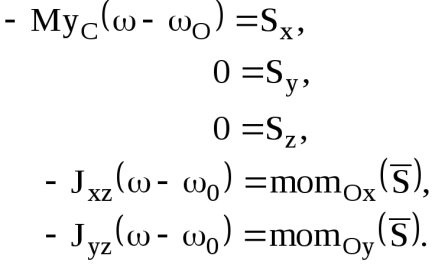 (23)
(23) Из второго и третьего уравнений (23) следует, что для отсутствия ударных реактивных импульсов необходимо, чтобы приложенный ударный импульс был направлен параллельно оси Оx, то есть перпендикулярно плоскости yОz, которая проходит через ось вращения и центр масс АТТ (рис. 5).
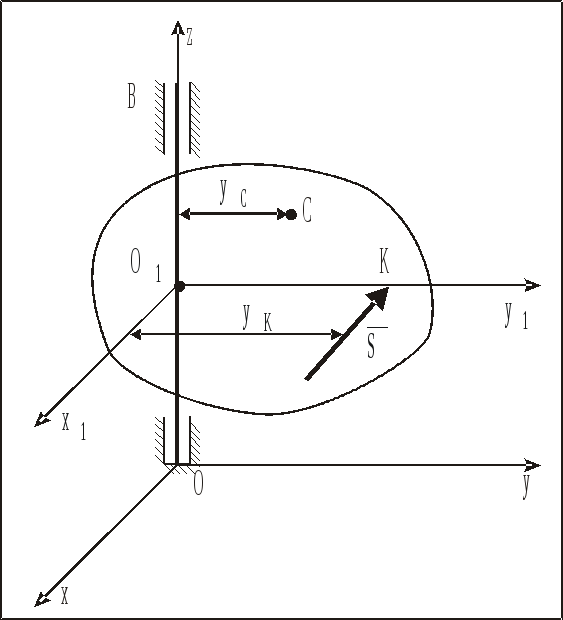 Рис. 5. [6]. | Так как систему координат можно выбрать произвольно, то выберем ее такой, чтобы ударный импульс В результате четвертое и пятое из уравнений (23) дадут следующие условия [6]: |
то есть ось вращения z для точки О1 должна быть главной осью инерции.
Следовательно, для отсутствия ударных реактивных импульсов необходимо расположить ударный импульс
Первое соотношение (23) примет вид [6]:

