Файл: Конспект лекций для магистрантов специальности 6М070200 Автоматизация и управление.doc
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 27.04.2024
Просмотров: 354
Скачиваний: 0
СОДЕРЖАНИЕ
Модуль 1. Моделирование и идентификация статических характеристик объектов
Тема 2 Математические модели объектов идентификации
Лекция 2 Основнные понятия и терминология дисциплины
Лекция 3 Постановка задачи моделирования и идентификации статических характеристик объектов
Лекция 4 Основные характеристики случайных величин
Лекция 5 Оценка статистических показателей(часть1)
Лекция 6 Оценка статистических показателей(часть2)
Лекция 7 Статические модели в форме управления регрессии и методы их определения (часть 1)
Лекция 8 Статические модели в форме управления регрессии и методы их определения (часть 2)
Лекция 9 Статические модели в форме управления регрессии и методы их определения (часть 3)
Лекция 10 Статические модели в форме управления регрессии и методы их определения (часть 4)
Лекция 11 Методы планирования эксперимента (часть 1)
Лекция 12 Методы планирования эксперимента (часть 2)
Лекция 13 Методы планирования эксперимента (часть 3)
Лекция 14 Методы планирования эксперимента (часть 4)
Лекция 15 Методы планирования эксперимента (часть 5)
Модуль 2. Моделирование и идентификация динамических характеристик объектов
Тема3 Моделирование и идентификация динамических характеристик объектов
Лекция 16 Множество моделей, структуры моделей (часть 1)
Лекция 17 Множество моделей, структуры моделей (часть 2)
Лекция 18 Идентификация динамических систем
Лекция 19 Определение частотных характеристик.
Лекция 20 Определение переходных характеристик
Тема 4 Параметрическая статистическая идентификация
Лекция 21 Основные характеристики времянных рядов
Лекция 22 Параметрическая статистическая идентификация (часть 1)
Лекция 23 Параметрическая статистическая идентификация (часть 2)
Лекция 24 Параметрическая статистическая идентификация (часть 3)
Лекция 25 Параметрическая статистическая идентификация (часть 4)
Лекция 26 Параметрическая статистическая идентификация (часть 5)
Лекция 27 Параметрическая статистическая идентификация (часть 6)
Тема 4 Специальное программное обеспечение задач моделирования
Лекция 28 Специальное программное обеспечение задач моделирования (часть 1)
Лекция 29 Сециальное программное обеспечение задач моделирования (часть 2)
Лекция 30 Сециальное программное обеспечение задач моделирования (часть 2)
Приложение А. Условные обозначения
Приложение Б. Глоссарий. Основная терминология
Методическое обеспечение дисциплины и ТСО.
Учебники, учебные пособия, методические указания, конспекты лекций, справочники и др.
Плакаты, слайды, видео- и телефильмы, программы для ЭВМ (номера, полные названия)
Лекция 11 Методы планирования эксперимента (часть 1)
Планирование эксперимента (англ. experimental design techniques) — комплекс мероприятий, направленных на эффективную постановку опытов. Основная цель планирования эксперимента – достижение максимальной точности измерений при минимальном количестве проведенных опытов и сохранении статистической достоверности результатов.
Планирование эксперимента применяется при поиске оптимальных условий, построении интерполяционных формул, выборе значимых факторов, оценке и уточнении констант теоретических моделей и др.
Полный факторный эксперимент (ПФЭ) – совокупность нескольких измерений, удовлетворяющих следующим условиям:
-
количество измерений составляет 2n, где n – количество факторов; -
каждый фактор принимает только два значения – верхнее и нижнее; -
в процессе измерения верхние и нижние значения факторов комбинируются во всех возможных сочетаниях;
Преимуществами полного факторного эксперимента являются
-
простота решения системы уравнений оценивания параметров; -
статистическая избыточность количества измерений, которая уменьшает влияние погрешностей отдельных измерений на оценку параметров.
Основные недостатки классического регрессионного анализа: корреляция между коэффициентами; трудности в оценке ошибки; необходимость проведения большого количества опытов; трудности при определении коэффициентов bi вручную.
В основе методов статистического плана эксперимента (ПЭ) лежит использование упорядоченного плана расположения точек в факторном пространстве и использование новой безразмерной системы координат. Использование методов ПЭ позволяет устранить практически все недостатки регрессионного анализа.
Методы планирования эксперимента позволяют строить как статические, так и динамические модели. Те и другие могут быть определены аналитическими и экспериментально- статистическими методами. Теория оптимального эксперимента на начальном этапе развития имитационного моделирования применялась преимущественно при построении моделей статических объектов. Что
касается построения динамических моделей, то методология построения базировалась в рамках пассивного эксперимента, когда идентификация велась в режиме нормального функционирования объекта. Однако, постепенно стали применять и активные методы идентификации с использованием специальных тестирующих сигналов. В качестве таких сигналов использовали псевдослучайные сигналы.
Основные понятия на которые надо обратить внимание: факторы (входы, воздействия – они не должны быть коррелированны), уровни (дискретные значения, принимаемые факторами), матрица ПЭ (собственно план), методы математической обработки.
Основные принципы планирования эксперимента (ПЭ).
Пассивным экспериментом называют эксперимент, в котором регистрация входных и выходных данных осуществляется в рабочем режиме, не используя дополнительных вмешательств. Он применяется тогда, когда структура модели хорошо известна и ее адекватность не вызывает сомнений (когда решаются задачи параметрической идентификации).
Активный эксперимент предполагает особую программу (план) проведения наблюдений таких, что позволяют по результатам исследований дополнительно оценить структуру модели.
Факторами активного эксперимента называют переменные, по которым возможно проводить управление и которые участвуют в построении модели (хi).
Каждый из факторов может принимать различные значения, которые называются уровнями. На практике, количество уровней – это бесконечное количество или непрерывный ряд уровней
Фиксированный набор уровней называется состоянием факторов.
План – это программа проведения эксперимента, позволяющая использовать все факторы на всех уровнях. Если план содержит всевозможные сочетания факторов и уровней, то такой план называют полным.
Если р – общее количество уровней; к – количество факторов, то полный план эксперимента будет включать в себя следующее количество экспериментов:
.
В методах ПЭ используются кодированные (безразмерные) параметров. Они соответствуют переносу начала координат в точку
Интервал варьирования по оси
Для перехода от физических (натуральных) переменных
а для обратного перехода
Например, пусть
при
Для безразмерных переменных в ПФЭ верхний уровень равен +1, а нижний –1, координаты центра плана равны нулю. В некоторых планах (см. ниже) используются безразмерные значения факторов
В приведенном примере при
Отметим, что введение безразмерной системы координат необходимо только для облегчения обработки результатов вручную. Если использовать для поиска решения матричное уравнение (4.15), то сразу получаем решение с найденными коэффициентами в натуральном (физическом) масштабе.
В полном факторном эксперименте (ПФЭ) обеспечивается проведение опытов при всех возможных сочетаниях значений факторов на всех уровнях варьирования, используются значения факторов только равные +1 и –1.
Каждому фиксированному набору уровню факторов соответствует определённая точка в многомерном пространстве, называемая факторным пространством. Эксперименты не могут быть реализованы во всех точках факторного пространства, а лишь в принадлежащих допустимой области, как это например оказано для случая двух факторов Х1 и Х2 (см. рисунок 11.1).
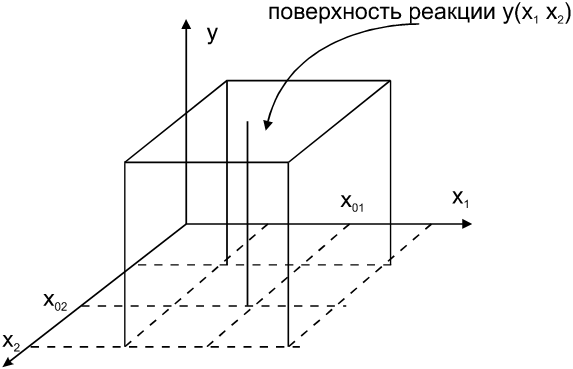
Рисунок 11.1-. Геометрическое представление поверхности реакции
Необходимое число опытов ПФЭ:
чаще используют
Таблица 11.1
Необходимое количество опытов
| Количество факторов –k | 3 | 4 | 5 | 6 | 7 |
| Количество опытов – N | 8 | 16 | 32 | 64 | 128 |
| Кол. коэф. линейной модели - L | 4 | 5 | 6 | 7 | 8 |
| Число степеней свободы - f | 4 | 11 | 26 | 57 | 120 |
Матрица ПФЭ для 3-х факторов
Таблица 11.2
Матрица ПФЭ для 3-х факторов
| № опыта | | | | | |
| 1 | +1 | –1 | –1 | –1 | |
| 2 | +1 | +1 | –1 | –1 | |
| 3 | +1 | –1 | +1 | –1 | |
| 4 | +1 | +1 | +1 | –1 | |
| 5 | +1 | –1 | –1 | +1 | |
| 6 | +1 | +1 | –1 | +1 | |
| 7 | +1 | –1 | +1 | +1 | |
| 8 | +1 | +1 | +1 | +1 | |
План эксперимента понимается так. Например, для первого опыта:
Столбец
Ортогональность матрицы планирования приводит к диагональности матрицы
(напомним, что для можно сразу использовать уравнение (4.15).
Матрица ПЭ, приведенная в таблице 6.2. позволяет определить коэффициенты линейного уравнения регрессии:
В принципе имеющиеся степени свободы позволяют определить коэффициенты уравнения регрессии с учетом эффектов взаимодействия вида:

