Файл: Контрольная работа по дисциплине "Метрология, стандартизация и сертификация".doc
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 27.04.2024
Просмотров: 52
Скачиваний: 0
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
СОДЕРЖАНИЕ
1.1 Расчёт абсолютной, относительной и приведенной погрешностей результатов измерений
1.2 Расчёт аддитивных и мультипликативных составляющих погрешностей результатов измерений
2. Определение систематических погрешностей в исходном ряду измерений
2.1 Метод последовательных разностей
2.2 Определение грубых погрешностей в исходном ряду измерений

Рис.3.4. График абсолютной мультипликативной погрешности
Исходя из того, что использованное средство измерения обладает единой для всей шкалы средней относительной погрешностью
Рассчитаем относительные аддитивные составляющие погрешности (
Δа= 0,075 м и зависимость вида:
Результаты расчётов относительных аддитивных составляющих погрешностей (
Таблица 3.2.
Результаты расчётов относительных составляющих погрешностей измерений.
| № члена ряда | | | | |
| 1 | 1 | 7,45 | 0,075 | 0 |
| 2 | 2,2 | 7,45 | 0,034 | 0,0409 |
| 3 | 12,2 | 7,45 | 0,006 | 0,0689 |
| 4 | 22,2 | 7,45 | 0,003 | 0,0716 |
| 5 | 32,2 | 7,45 | 0,0023 | 0,0727 |
| 6 | 42,2 | 7,45 | 0,0017 | 0,0732 |
| 7 | 52,2 | 7,45 | 0,0014 | 0,0735 |
| 8 | 62,2 | 7,45 | 0,0012 | 0,0738 |
| 9 | 72,2 | 7,45 | 0,0010 | 0,0739 |
| 10 | 82,2 | 7,45 | 0,0009 | 0,0741 |

Рис.3.5. График относительной аддитивной погрешности
Используя результаты расчётов абсолютной мультипликативной составляющей погрешности, которые приведены в таблице 3.1, рассчитаем относительные аддитивные составляющие погрешности (
Результаты расчётов относительных мультипликативных составляющих погрешностей (

Рис.3.6. График относительной мультипликативной погрешности
2. Определение систематических погрешностей в исходном ряду измерений
По характеру (закономерности) изменения погрешности измерений подразделяются на систематические, случайные и грубые (промахи).
Систематические погрешности Δс – составляющие погрешности; измерений, остающиеся постоянными или закономерно изменяющиеся при многократных (повторных) измерениях одной и той же величины в одних и тех же условиях. Такие погрешности могут быть выявлены путем детального анализа возможных их источников и уменьшены (применением более точных приборов, калибровкой приборов с помощью рабочих мер и пр.). Однако полностью их устранить нельзя.
Известны некоторые общие методы значительного уменьшения таких погрешностей.
По характеру изменения во времени систематические погрешности подразделяются на постоянные (сохраняющие величину и знак), прогрессирующие (возрастающие или убывающие во времени), периодические, а также изменяющиеся во времени по сложному непериодическому закону.
Основные из этих погрешностей – прогрессирующие.
Прогрессирующая (дрейфовая) погрешность – это непредсказуемая погрешность, медленно меняющаяся во времени.
Отличительные особенности прогрессирующих погрешностей:
- их можно скорректировать поправками только в данный момент времени, а далее вновь непредсказуемо изменяются;
– изменения прогрессирующих погрешностей во времени – нестационарный (характеристики которого изменяются во времени; см. далее) случайный процесс, и поэтому в рамках хорошо разработанной теории стационарных случайных процессов они могут быть описаны лишь с известными оговорками.
Отличительным признаком постоянной и переменной систематической погрешности является то, что они могут быть предсказаны, обнаружены и благодаря этому почти полностью устранены введением соответствующей поправки.
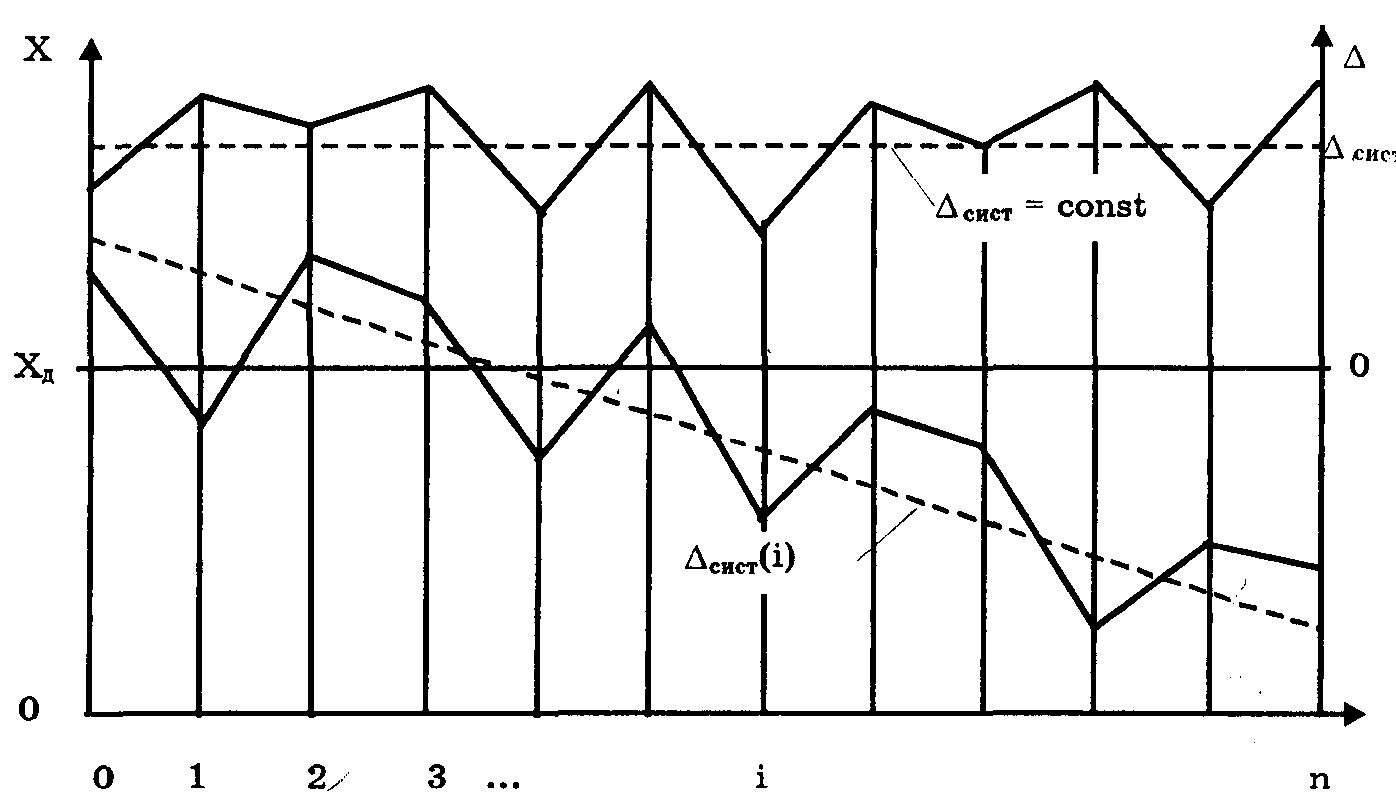
Рис.4.1. Постоянная и переменная систематические погрешности
Способы обнаружения систематических погрешностей
При проведении измерений стараются в максимальной степени исключить или учесть влияние СП. Это возможно:
- при устранении источников погрешностей до начала измерений;
- внесением известных поправок в результат измерения;
- путем оценки границ неисключенных СП.
Постоянная составляющая СП не может быть ни выявлена, ни найдена методами совместной обработки результатов измерений. Однако она не может исказить ни показатели точности измерений, характеризующие случайную погрешность, ни результат нахождения переменной составляющей СП.
Постоянные систематические погрешности могут быть обнаружены лишь путем сравнения результатов измерений с другими, полученными с помощью более высокоточных методов и средств. Иногда эти погрешности могут быть устранены специальными приемами проведения процесса измерений.
Наиболее универсальным способом исключения неизвестных постоянных систематических погрешностей является способ их рандомизации. Суть этого способа состоит в том, что одна и та же величина измеряется различными методами (приборами). Систематические погрешности каждого из них для всей совокупности являются разными случайными величинами. Вследствие этого при увеличении числа используемых методов (приборов) систематические погрешности взаимно компенсируются.
Наличие существенной переменной СП искажает оценки характеристик случайной погрешности и аппроксимацию ее распределения. Поэтому она должна обязательно выявляться и исключаться из результатов измерений и учитываться в оценках СП.
Для выявления систематических погрешностей наиболее часто используют один из следующих трёх методов: графический, метод последовательных разностей, метод дисперсионного анализа. Рассмотрим и используем на практике, согласно задания на контрольную работу, метод последовательных разностей.
2.1 Метод последовательных разностей
Этот метод применим для обнаружения изменяющейся во времени систематической погрешности. Дисперсию результатов наблюдений можно оценить двумя способами:
Обычным
 (4.1)
(4.1)или вычислением суммы квадратов последовательных (в порядке последовательности измерений) разностей
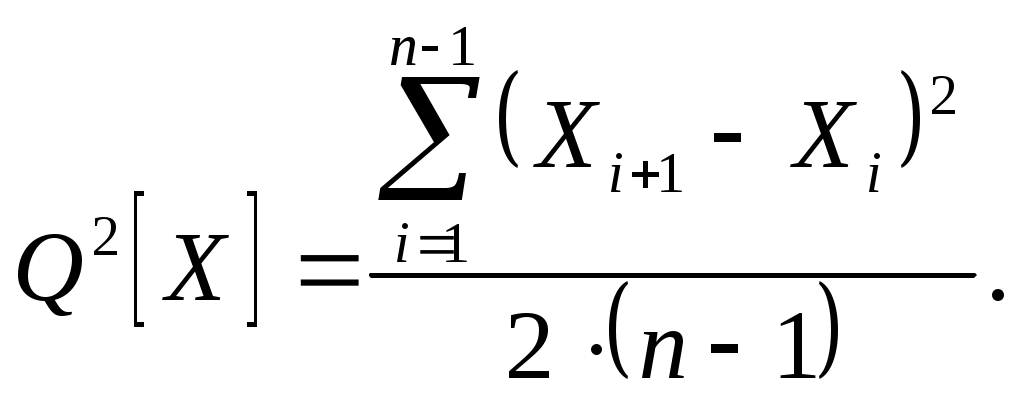 (4.2)
(4.2)Если в процессе измерений происходило смещение центра группирования результатов наблюдений, т.е. имела место временная систематическая погрешность, то
является критерием для обнаружения систематических смещений центра группирования результатов наблюдений.
Критическая область для этого критерия (критерия Аббе) определяется как
Таблица 4.1 Значения критерия Аббе

Для заданного в задании ряда результатов измерений линейного размера L элемента конструкции строящегося здания (см. таблицу № 2.1) вначале вычислим среднее арифметическое значений этого ряда:
 (м). (4.4)
(м). (4.4)Полученное среднее арифметическое значение, как и другие промежуточные результаты для применения критерия Аббе, сведены в таблицу 4.2.
Таблица 4.2.
Промежуточные результаты для применения критерия Аббе

