Файл: Контрольная работа по дисциплине "Метрология, стандартизация и сертификация".doc

Применяя полученные значения суммарной абсолютной погрешности (Δсi), рассчитаем среднее значение абсолютной погрешности по зависимости вида:

(2.4)

Подставив в формулу (2.4) необходимые данные из таблицы 2.2, получим м.

Используя рассчитанные значения суммарной абсолютной погрешности (Δ_сi), рассчитываются суммарные относительные погрешности измерений (δ_сi), применяя зависимость вида (2.2):
Таблица 2.3

Суммарные относительные погрешности

№ измерения		№ измерения		№ измерения
1	0,08	11	0,15	21	-0,22
2	0,00	12	0,21	22	0,00
3	-0,38	13	0,08	23	0,08
4	0,21	14	0,27	24	0,21
5	-0,22	15	0,21	25	0,27
6	0,08	16	0,31	26	0,21
7	0,15	17	0,08	27	0,35
8	-0,10	18	0,00	28	0,21
9	0,08	19	-0,10	29	0,27
10	0,00	20	-0,57	30	0,27

---

Применяя полученные значения суммарной относительной погрешности ( _сi), рассчитаем среднее значение абсолютной погрешности по зависимости вида:

(2.5)

Подставив в формулу (2.5) необходимые данные из таблицы 2.3, получим , что в процентах соответствует % .

Для расчёта приведенной погрешности результатов измерений, в соответствии с формулой (2.3), необходимо знание нормирующего значения , которое, в соответствии с заданием, не определено. Поэтому, учитывая реальные линейные размеры элемента конструкции строящегося здания, допустим, что средство измерения этих размеров имеет конечное значение шкалы, например, 100 м, т.е. X_N=100м.

Тогда средняя приведенная погрешность, с учётом выше рассчитанного значения Δ_ср=0,28 м, составит:

---

1.2 Расчёт аддитивных и мультипликативных составляющих погрешностей результатов измерений

По зависимости абсолютной погрешности от значений измеряемой величины различают погрешности (рис. 3.1):

• 
  аддитивные , не зависящие от измеряемой величины;
  
• 
  мультипликативные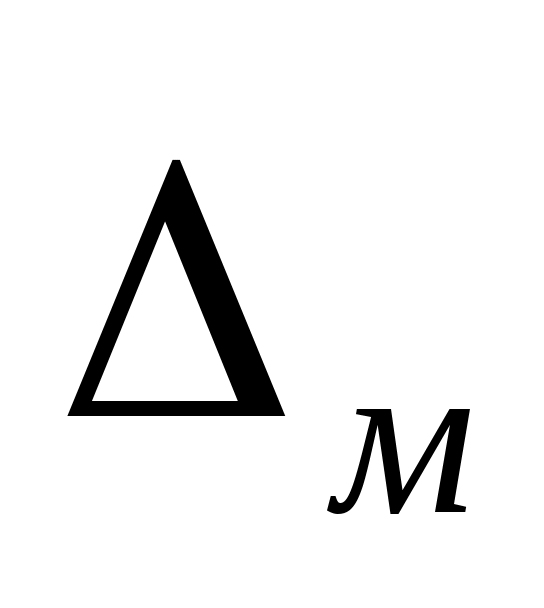 , которые прямо пропорциональны измеряемой величине;
  
• 
  нелинейные , имеющие нелинейную зависимость от измеряемой величины.
  

Эти погрешности применяют в основном для описания метрологических характеристик СИ. Разделение погрешностей на аддитивные, мультипликативные и нелинейные весьма существенно при решении вопроса о нормировании и математическом описании погрешностей СИ.

Примеры аддитивных погрешностей – от постоянного груза на чашке весов, от неточной установки на нуль стрелки прибора перед измерением, от термо-ЭДС в цепях постоянного тока. Причинами возникновения мультипликативных погрешностей могут быть: изменение коэффициента усиления усилителя, изменение жесткости мембраны датчика манометра или пружины прибора, изменение опорного напряжения в цифровом вольтметре.

Данные разновидности погрешностей иногда называют также так:

• 
  аддитивные - погрешность нуля;
  
• 
  мультипликативные - погрешность крутизны характеристики;
  
• 
  нелинейные - погрешность нелинейности.
  

Рис. 3.1. Аддитивная (а), мультипликативная (б) и нелинейная (в) погрешности
В связи с тем, что аддитивная и мультипликативная составляющие погрешности характерны для средства измерения, причём в диапазоне измеряемых величин, то исходя из заданного истинного (действительного) значения линейного размера элемента конструкции (2,2 м), допустим, что использованное средство измерений, позволяет производить измерения в диапазоне от 1 м до 100 м, причём обладает единой для всей шкалы средней относительной погрешностью δ

---

_ср=7,45%, которое рассчитано по формуле (2.5) в 2-ом разделе данной работы. Исходя из выбранного диапазона измерений средства измерений (1м – 100м), возьмём из него, например, 10 равноудалённых фиксированных (эталонных) значений линейного размера элемента конструкции, включая заданное истинное (действительное) значение, равное 2,2 метра. В результате ряд измеряемых эталонных значений линейных размеров L_эт, использованным средством измерения, будет иметь вид: 1; 2,2; 12,2; 22,2; 32,2; 42,2; 52,2; 62,2; 72,2; 82,2 (м).

Используя выражение (2.5), можно определить значения суммарной абсолютной погрешности для всех членов ряда L_эт, а именно:

3.1)

Рассчитанные значения суммарной абсолютной погрешности для всех членов ряда, с учётом выполнения правил округления результатов измерений и погрешностей измерений (приведены в Приложении 1), представлены в таблице 3.1.
Таблица 3.1. Результаты расчетов суммарной, аддитивной и мультипликативной абсолютных погрешностей

№ члена ряда				Δа, м
1	1	7,45	0,07	0,075	0
2	2,2	7,45	0,16	0,075	0,089
3	12,2	7,45	0,91	0,075	0,83
4	22,2	7,45	1,65	0,075	1,58
5	32,2	7,45	2,40	0,075	2,32
6	42,2	7,45	3,14	0,075	3,07
7	52,2	7,45	3,89	0,075	3,81
8	62,2	7,45	4,63	0,075	4,56
9	72,2	7,45	5,38	0,075	5,30
10	82,2	7,45	6,12	0,075	6,05

---

Используя результаты расчётов суммарной абсолютной погрешности и ряд измеряемых эталонных значений линейных размеров , строится график (см. Рис.3.2) зависимости , при этом апроксимируются точки по которым он строится. На осях графика обозначаются начальные и конечные значения диапазона измерения средства измерения (L_эн=1 м и L_эк=100 м) и максимального значения суммарной погрешности Δ_с (Δ_ск =6,12 м).

На полученном графике (Рис.3.2) выделяется аддитивная составляющая (Δ_а) суммарной абсолютной погрешности (Δ_с), которая равна суммарной абсолютной погрешности при минимальном (начальном) значении эталонных значений линейных размеров (в начале диапазона измерений СИ), т.е. Δ_а= 0,075 м.



Рис.3.2 График суммарной абсолютной погрешности
Строится график (Рис.3.3) зависимости абсолютной аддитивной погрешности Δ_а=f(L_ЭТ._i), который представляет собой прямую параллельную оси абсцисс, проходящей из точки с ординатой Δ_а= 0,075 м.



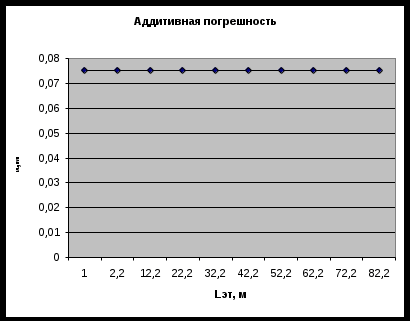
Рис.3.3. График абсолютной аддитивной погрешности

На полученном графике (см. Рис.3.2) зависимости , выделяется график мультипликативной составляющей Δ_м= f(L_ЭТ), который идёт параллельно графику суммарной абсолютной погрешности, но начинается не из точки с координатами (1; 0,07), а из точки с координатами (1; 0), т.к. , то и На осях графика обозначаются начальные и конечные значения диапазона изменения линейного размера L_ЭТ (L_эн=1 м и L_эк=82,2 м) и максимального значения мультипликативной погрешности Δ_м (Δ_мк=6,05 м). Результаты расчета абсолютной мультипликативной погрешности приведены в таблице 3.1, а график на рисунке 3.4.

---