Файл: Контрольная работа по дисциплине "Метрология, стандартизация и сертификация".doc
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 27.04.2024
Просмотров: 56
Скачиваний: 0
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
СОДЕРЖАНИЕ
1.1 Расчёт абсолютной, относительной и приведенной погрешностей результатов измерений
1.2 Расчёт аддитивных и мультипликативных составляющих погрешностей результатов измерений
2. Определение систематических погрешностей в исходном ряду измерений
2.1 Метод последовательных разностей
2.2 Определение грубых погрешностей в исходном ряду измерений
2.5 Критерий Шарлье
Критерий Шарлье используется при числе результатов наблюдений n>5 (5…100). При использовании данного критерия для сомнительного результата Xi измерений проверяется выполнение неравенства вида:
Значения критерия Шарлье (tш) определяются по табл.5.2. В случае выполнения неравенства (5.5) сомнительный результат отбрасывается из ряда наблюдений.
Таблица 5.2. Значения критерия Шарлье
| n | 5 | 10 | 20 | 30 | 40 | 50 | 100 |
| | 1,3 | 1,65 | 1,96 | 2,13 | 2,24 | 2,32 | 2,58 |
Используя вышеприведенную методику по выявлению грубых погрешностей с помощью критерия Шарлье, определим, имеются ли промахи в ряду измерений линейного размера L элемента конструкции строящегося здания, приведенные в таблице 2.1. Для этого, применяя выражения для вычисления среднего арифметического результатов измерений
Тогда, для проверки неравенства (5.5) при сомнительном результате измерений Xi, которым является максимальное значение результатов измерений 6,8 м (см. 27-й результат измерений в таблице 2.1) вычислим левую и правую части этого неравенства, используя таблицу 5.2 (при "n" =30 критерий "tш" равен 2,13), а именно:
Полученные значения левой и правой частей неравенства (5.5), говорят о том, что это неравенство не выполняется (0,92˂2,057), а, следовательно, подверженный сомнению максимальный результат измерений равный 6,8 м, не является результатом грубой погрешности и не может быть исключён из ряда наблюдений. Все остальные результаты измерений также не могут быть отнесены к промахам и не могут быть отброшены из ряда измерений, так как их значения меньше максимального результата измерений 3,4 м.
2.6 Критерий Диксона
Это чрезвычайно удобный и достаточно мощный (с малыми вероятностями ошибок) критерий, используемый при n=4…30. Его особенность заключается в том, что результаты измерений раскладываются в вариационный возрастающий ряд. Х1 … Хn.
 . (5.7)
. (5.7)Расчетное значение КД сравнивается с табличным значением Кα (см. таблицу 5.3), которое зависит от уровня значимости α. В случае выполнения неравенства КД ˃Кα сомнительный результат измерений Хn отбрасывается.
Используя вышеприведенную методику по выявлению грубых погрешностей с помощью критерия Диксона, определим, имеются ли промахи в ряду измерений линейного размера L элемента конструкции строящегося здания, приведенные в таблице 2.1. Для этого результаты измерений таблицы 2.1 представим вариационным возрастающим рядом, который примет вид таблицы 5.4.
Таблица 5.3.
Значения критерия Диксона
| n | | |||
| 0,10 | 0,05 | 0,02 | 0,01 | |
| 4 | 0,68 | 0,76 | 0,85 | 0,89 |
| 6 | 0,48 | 0,56 | 0,64 | 0,70 |
| 8 | 0,40 | 0,47 | 0,54 | 0,59 |
| 10 | 0,35 | 0,41 | 0,48 | 0,53 |
| 14 | 0,29 | 0,35 | 0,41 | 0,45 |
| 16 | 0,28 | 0,33 | 0,39 | 0,43 |
| 18 | 0,26 | 0,31 | 0,37 | 0,41 |
| 20 | 0,24 | 0,30 | 0,36 | 0,39 |
| 30 | 0,22 | 0,26 | 0,31 | 0,34 |
Таблица 5.4 Результаты измерений линейного размера L (в метрах) элемента конструкции строящегося здания с учётом порядкового номера студента в форме вариационного возрастающего ряда
| № измерения | Li | № измерения | Li | № измерения | Li |
| 1 | 2,8 | 11 | 4,8 | 21 | 5,6 |
| 2 | 3,2 | 12 | 4,8 | 22 | 5,6 |
| 3 | 3,6 | 13 | 4,8 | 23 | 5,6 |
| 4 | 3,6 | 14 | 4,8 | 24 | 5,6 |
| 5 | 4,0 | 15 | 4,8 | 25 | 6,0 |
| 6 | 4,0 | 16 | 4,8 | 26 | 6,0 |
| 7 | 4,4 | 17 | 5,2 | 27 | 6,0 |
| 8 | 4,4 | 18 | 5,2 | 28 | 6,0 |
| 9 | 4,4 | 19 | 5,6 | 29 | 6,4 |
| 10 | 4,4 | 20 | 5,6 | 30 | 6,8 |
Используя результаты таблицы 5.4, рассчитаем значение критерия Диксона "КД" по формуле (5.7), приняв за "n" равное 30 (последний номер члена вариационного ряда), а именно:
Сравнивая расчётное значение критерия Диксона "КД=0,10" с любым из табличных значений Кα при любом уровне значимости
Применение рассмотренных критериев требует осмотрительности и учета объективных условий измерений. Конечно, оператор должен исключить результат наблюдения с явной грубой погрешностью и выполнить новое измерение. Но он не имеет права отбрасывать более или менее резко отличающиеся от других результаты наблюдений. В сомнительных случаях лучше сделать дополнительные измерения (не взамен сомнительных, а кроме них) и затем привлекать на помощь рассмотренные выше статистические критерии.
Выводы
Выполненная контрольная работа позволила:
-
произвести расчёт абсолютной, относительной и приведенной погрешностей результатов измерений линейного размера конструкции строящегося здания, средние значения которых составили соответственно: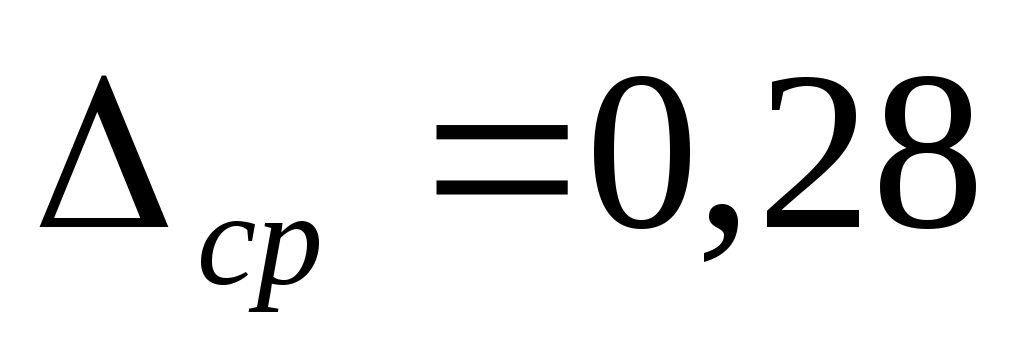 ,
,  ,
, 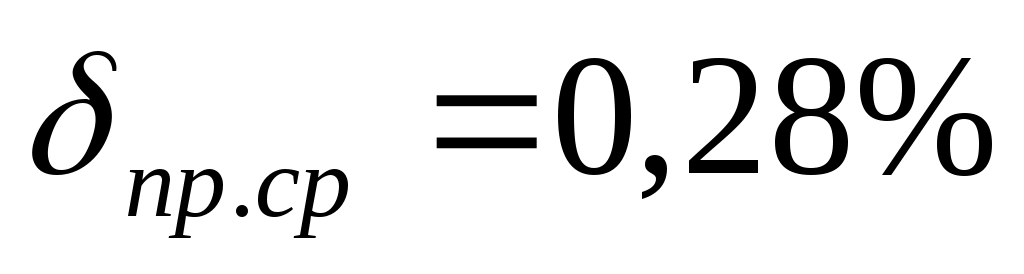 .
. -
рассчитать и построить графики суммарной абсолютной и относительной погрешностей результатов измерений линейного размера конструкции строящегося здания, выделить из них и построить графики аддитивной и мультипликативной составляющих погрешностей; -
установить факт отсутствия систематических погрешностей при уровне значимости α=0,001 и α=0,01 и присутствии систематических погрешностей при уровне значимости α=0,05 в исходном ряду измерений линейного размера конструкции строящегося здания, с помощью метода последовательных разностей; -
установить факт отсутствия грубых погрешностей в исходном ряду измерений линейного размера конструкции строящегося здания, с помощью критерия Граббса, критерия "трёх сигм", критерия Шарлье и критерия Диксона.
Список использованной литературы
1. Сергеев А.Г., Крохин В.В. Метрология: Учеб.пособие для вузов. М.: Логос,2000.-408с.
2. Метрология и электрорадиоизмерения в телекоммуникационных системах: учебник для вузов-В.И. Нефедов, В.И. Хахин, Е.В. Федорова и др,;Под ред. В.И. Нефедова.-М.:Высш.шк.,2001-381 с.
3. Алиев Т.М.,Тер-Хачатуров А.А. Измерительная техника: Учеб. пособие для техн. вузов.-М.:Высш.шк.,1991.-384с.
4. Методические указания к практическим занятиям по курсу "Теоретическая метрология" / Под ред. А.Г. Сергеева. Сост.: А.Г. Сергеев и др., Владим. гос. ун-т; Владимир, 1997, 64 с.
5. Куприянов В.Е. Общая теория измерений: в 2 ч. Ч.2.Методы измерений. Математические модели. Погрешности и обработка результатов измерений: учеб.пособие/В.Е. Куприянов, Э.Ф. Касаткина; Владим.гос.ун-т – Владимир: ВлГУ,2005. -148 с.
Приложение 1.
Правила округления результатов измерений
1. Погрешность указывается двумя значащими цифрами, если первая из них равна единице или двойке, и одной, если первая цифра равна трем и более.
2. Результат измерения округляется до того же десятичного знака, которым оканчивается округленное значение абсолютной погрешности. Если десятичная дробь в числовом значении результата измерений оканчивается нулями, то нули отбрасываются до того разряда, который соответствует разряду числового значения погрешности.
3. Если цифра старшего отбрасываемого разряда меньше пяти, то остальные цифры числа не меняются. Лишние цифры в целых числах заменяются нулями, а в десятичных дробях отбрасываются.
4. Если цифра старшего из отбрасываемых разрядов больше или равна пяти, но за ней следуют отличные от нуля цифры, то последнюю оставляемую цифру увеличиваем на единицу.
5. Если отбрасываемая цифра равна пяти, а следующие за ней цифры неизвестны или нули, то последнюю сохраняемую цифру числа не изменяют, если она четная, и увеличивают на единицу, если она не четная.
6. Округление производится в окончательном ответе, а все предварительные расчеты проводят с 2-3 лишними знаками.

