Файл: Контрольная работа по дисциплине "Метрология, стандартизация и сертификация".doc
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 27.04.2024
Просмотров: 57
Скачиваний: 0
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
СОДЕРЖАНИЕ
1.1 Расчёт абсолютной, относительной и приведенной погрешностей результатов измерений
1.2 Расчёт аддитивных и мультипликативных составляющих погрешностей результатов измерений
2. Определение систематических погрешностей в исходном ряду измерений
2.1 Метод последовательных разностей
2.2 Определение грубых погрешностей в исходном ряду измерений
| № измерения | X=Li,м | | | | |
| 1 | 2,4 | | | -0,08 | 0,0064 |
| 2 | 2,2 | -0,2 | 0,04 | -0,28 | 0,0784 |
| 3 | 1,6 | -0,6 | 0,36 | -0,88 | 0,7744 |
| 4 | 2,8 | 1,2 | 1,44 | 0,32 | 0,1024 |
| 5 | 1,8 | -1 | 1 | -0,68 | 0,4624 |
| 6 | 2,4 | 0,6 | 0,36 | -0,08 | 0,0064 |
| 7 | 2,6 | 0,2 | 0,04 | 0,12 | 0,0144 |
| 8 | 2,0 | -0,6 | 0,36 | -0,48 | 0,2304 |
| 9 | 2,4 | 0,4 | 0,16 | -0,08 | 0,0064 |
| 10 | 2,2 | -0,2 | 0,04 | -0,28 | 0,0784 |
| 11 | 2,6 | 0,4 | 0,16 | 0,12 | 0,0144 |
| 12 | 2,8 | 0,2 | 0,04 | 0,32 | 0,1024 |
| 13 | 2,4 | -0,4 | 0,16 | -0,08 | 0,0064 |
| 14 | 3,0 | 0,6 | 0,36 | 0,52 | 0,2704 |
| 15 | 2,8 | -0,2 | 0,04 | 0,32 | 0,1024 |
| 16 | 3,2 | 0,4 | 0,16 | 0,72 | 0,5184 |
| 17 | 2,4 | -0,8 | 0,64 | -0,08 | 0,0064 |
| 18 | 2,2 | -0,2 | 0,04 | -0,28 | 0,0784 |
| 19 | 2,0 | -0,2 | 0,04 | -0,48 | 0,2304 |
| 20 | 1,4 | -0,6 | 0,36 | -1,08 | 1,1664 |
| 21 | 1,8 | 0,4 | 0,16 | -0,68 | 0,4624 |
| 22 | 2,2 | 0,4 | 0,16 | -0,28 | 0,0784 |
| 23 | 2,4 | 0,2 | 0,04 | -0,08 | 0,0064 |
| 24 | 2,8 | 0,4 | 0,16 | 0,32 | 0,1024 |
| 25 | 3,0 | 0,2 | 0,04 | 0,52 | 0,2704 |
| 26 | 2,8 | -0,2 | 0,04 | 0,32 | 0,1024 |
| 27 | 3,4 | 0,6 | 0,36 | 0,92 | 0,8464 |
| 28 | 2,8 | -0,6 | 0,36 | 0,32 | 0,1024 |
| 29 | 3,0 | 0,2 | 0,04 | 0,52 | 0,2704 |
| 30 | 3,0 | 0 | 0 | 0,52 | 0,2704 |
| | 74,4 | | | | |
Используя выражение (4.2) и суммарный результат 4-го столбца таблицы 4.2, определим значение дисперсии
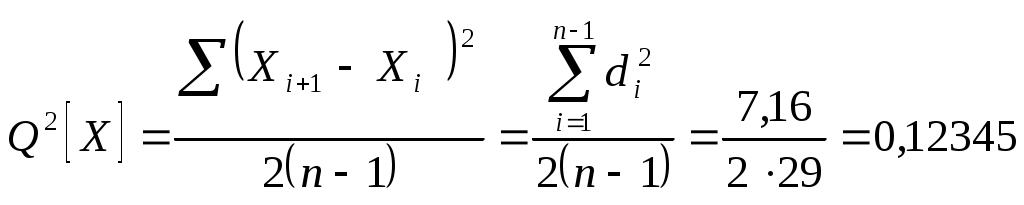
Применяя выражение 4.1 и суммарный результат 6 –го столбца таблицы 4.2, определим значение дисперсии

Тогда расчётное значение критерия Аббе с использованием выражения 4.3, будет равно:
Сравнивая расчётные значения критерия Аббе "А=0,529" с табличными "
2.2 Определение грубых погрешностей в исходном ряду измерений
Грубая погрешность или промах – это случайная погрешность результата отдельного измерения, входящего в ряд измерений, которая для данных условий резко отличается от остальных результатов этого ряда.
Источниками (причинами возникновения) грубых погрешностей могут быть:
1) ошибки, допущенные оператором во время измерений;
2) внезапные и кратковременные изменения условий измерения;
3) оставшиеся незамеченными неисправности в аппаратуре.
К наиболее распространённым грубым ошибкам, т.е. ошибкам допущенным оператором во время измерений, можно отнести:
- неправильный отсчет по шкале измерительного прибора, происходящий из-за неверного учета цены малых делений шкалы;
- неправильная запись результата наблюдений;
- неправильная запись значений отдельных мер использованного набора, например, гирь.
Критерии исключения грубых погрешностей.
Грубые погрешности, как правило, возникают при однократных измерениях и обычно устраняются путем повторных измерений.
Вопрос о том, содержит ли результат наблюдений грубую погрешность, решается общими методами проверки статистических гипотез. Проверяемая гипотеза состоит в утверждении, что результат xi, не содержит грубой погрешности, т.е. является одним из значений измеряемой величины. Пользуясь определенными статистическими критериями, пытаются опровергнуть выдвинутую гипотезу. Если это удается, то результат наблюдений рассматривают, как содержащий грубую погрешность, если нет – то не исключают.
Для выявления грубых погрешностей задаются вероятностью α того, что сомнительный результат действительно мог иметь место в данной совокупности результатов измерений. Эту вероятность α называют уровнем значимости; α=1-ρ
дов, где ρдов является доверительной вероятностью. Обычно α выбирают равным 0,100; 0,050; 0,010.
Так как в подавляющем большинстве случаев действительные значения параметров законов распределения результатов наблюдений и их погрешностей неизвестны, то мы рассмотрим здесь лишь критерии, основанные на статистических оценках этих параметров. Рассмотрим некоторые из существующих критериев.
2.3 Критерий Граббса
Этот критерий применяется для нормально распределенных результатов измерений. Задавшись уровнем значимости α, по таблице 5.1 с учетом числа измерений "n" находят tr.
Табличное значение этого коэффициента (tr) сравнивают с вычисленными значениями " t ", (для сомнительных результатов измерений "xi"), которые определяют по формуле:
Здесь и далее
 2)
2) среднее арифметическое результатов измерений и оценка среднего квадратического отклонения результата измерений.
Если окажется, что t
Используя вышеприведенную методику по выявлению грубых погрешностей, допустим, что результаты измерений подчинены нормальному закону распределения и определим, имеются ли промахи в ряду измерений линейного размера L элемента конструкции строящегося здания, приведенные в таблице 2.1. Для этого, применяя выражения для вычисления среднего арифметического результатов измерений
Таблица 5.1

Рассчитаем значение критерия Граббса для сомнительного результата измерений Xi, которым является максимальное значение результатов измерений 3,4 м (см. 27-й результат измерений в таблице 2.1) по формуле:
Тогда
Для нахождения табличного значения критерия Граббса (tr), вначале зададимся значением доверительной вероятности Рдов=0,999 и переведём его в проценты, так как в таблице №1 значение уровня значимости α=1–Рдов задано именно в %. Тогда значению Рдов=0,999 соответствует её процентное значение Рдов=99,9%, следовательно, α=1–Рдов=100%–99,9%=0,1%.
Войдя в таблицу при α=0,1% и при числе наблюдений n=30, найдём табличное значение критерия Граббса "tr" равным 3,672. Таким образом, получено неравенство вида: t < tr, (так как 1,9< 3,672). Это говорит о том, что подверженный сомнению максимальный результат измерений равный 3,4 м, не является результатом грубой погрешности и не может быть исключён из ряда наблюдений, а, следовательно, и все остальные результаты измерений также не могут быть отнесены к промахам и не могут быть отброшены из ряда измерений.
1 2 3 4 5 6
2.4 Критерий "трёх сигм"
Данный критерий применяется для результатов измерений, распределённых по нормальному закону. В этом случае считается, что результат, возникающий с вероятностью (уровнем значимости) α≤0,003, маловероятен и его можно квалифицировать промахом, т.е. сомнительный результат "xi" отбрасывается если
Входящие в данное выражение величины
Используя вышеприведенную методику по выявлению грубых погрешностей, допустим, что результаты измерений подчинены нормальному закону распределения и определим, имеются ли промахи в ряду измерений линейного размера L элемента конструкции строящегося здания, приведенные в таблице 2.1. Для этого, применяя выражения для вычисления среднего арифметического результатов измерений
Тогда, для проверки неравенства (5.3) при сомнительном результате измерений Xi, которым является максимальное значение результатов измерений 6,8 м (см. 27-й результат измерений в таблице 2.1) вычислим левую и правую части этого неравенства, а именно:
Полученные значения левой и правой частей неравенства (5.3), говорят о том, что это неравенство не выполняется (2,2˂5,716), а, следовательно, подверженный сомнению максимальный результат измерений равный 6,8 м, не является результатом грубой погрешности и не может быть исключён из ряда наблюдений. Все остальные результаты измерений также не могут быть отнесены к промахам и не могут быть отброшены из ряда измерений, так как их значения меньше максимального результата измерений 3,4 м.

