Файл: Лекция Принципы управления 2 Общие понятия 2 Лекция Статический режим сау 7.doc
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 02.05.2024
Просмотров: 161
Скачиваний: 0
СОДЕРЖАНИЕ
Лекция 2. Статический режим САУ
Лекция 3. Динамический режим САУ
3.1. Динамический режим САУ. Уравнение динамики
Лекция 4.Структурные схемы САУ
4.1. Эквивалентные преобразования структурных схем
4.2. САР напряжения генератора постоянного тока
Лекция 5.Временные характеристики
5.1. Понятие временных характеристик
5.2. Переходные характеристики элементарных звеньев
Лекция 6. Частотные характеристики
6.2. Частотные характеристики типовых звеньев
7.1. Частотные характеристики разомкнутых одноконтурных САУ
Лекция 8. Алгебраические критерии устойчивости
8.1. Понятие устойчивости системы
8.2. Алгебраические критерии устойчивости
Лекция 9. Частотные критерии устойчивости
9.2. Критерий устойчивости Михайлова
9.3. Критерий устойчивости Найквиста
Лекция 10.D-разбиение. Запас устойчивости
10.1. Понятие структурной устойчивости. АФЧХ астатических САУ
10.2. Понятие запаса устойчивости
10.3. Анализ устойчивости по ЛЧХ
11.1. Теоретическое обоснование метода D-разбиений
11.2. D-разбиение по одному параметру
11.3. Прямые методы оценки качества управления
Лекция 13. Частотные методы оценки качества
13.1. Теоретическое обоснование
13.2. Основные соотношения между ВЧХ и переходной характеристикой
14.2. Коррекция свойств САУ изменением параметров звеньев
Лекция 15. Включение корректирующих звеньев
15.1. Коррекция свойств САУ включением последовательных корректирующих звеньев
15.1.1. Включение интегрирующего звена в статическую САУ
15.2. Последовательная коррекция по задающему воздействию
Содержание
Содержание 1
Лекция 1. Принципы управления 2
1.1. Общие понятия 2
Лекция 2. Статический режим САУ 7
2.1. Основные виды САУ 7
Лекция 3. Динамический режим САУ 13
3.1. Динамический режим САУ. Уравнение динамики 13
3.3. Передаточная функция 15
3.4. Элементарные динамические звенья 16
Лекция 4.Структурные схемы САУ 18
4.1. Эквивалентные преобразования структурных схем 18
4.2. САР напряжения генератора постоянного тока 22
Лекция 5.Временные характеристики 25
5.1. Понятие временных характеристик 25
5.2. Переходные характеристики элементарных звеньев 27
5.2.1. Безынерционное (пропорциональное, усилительное) звено 27
5.2.2. Интегрирующее (астатическое) звено 27
5.2.3. Инерционное звено первого порядка (апериодическое) 28
5.2.4. Инерционные звенья второго порядка 28
5.2.5. Дифференцирующее звено 29
Лекция 6. Частотные характеристики 30
6.2. Частотные характеристики типовых звеньев 32
6.2.1. Безынерционное звено 33
6.2.2. Интегрирующее звено 33
6.2.3. Апериодическое звено 34
6.2.4. Инерционные звенья второго порядка 35
6.2.5. Правила построения ЧХ элементарных звеньев 35
Лекция 7.ЧХ разомкнутых САУ 36
7.1. Частотные характеристики разомкнутых одноконтурных САУ 36
7.2. Законы регулирования 39
Лекция 8. Алгебраические критерии устойчивости 41
8.1. Понятие устойчивости системы 41
8.2. Алгебраические критерии устойчивости 43
8.2.1. Необходимое условие устойчивости 44
8.2.1. Критерий Рауса 44
8.2.2. Критерий Гурвица 45
Лекция 9. Частотные критерии устойчивости 46
9.1. Принцип аргумента 46
9.2. Критерий устойчивости Михайлова 47
9.3. Критерий устойчивости Найквиста 48
Лекция 10.D-разбиение. Запас устойчивости 50
10.1. Понятие структурной устойчивости. АФЧХ астатических САУ 50
10.2. Понятие запаса устойчивости 52
10.3. Анализ устойчивости по ЛЧХ 53
Лекция 11. Качество САУ 55
11.1. Теоретическое обоснование метода D-разбиений 55
11.2. D-разбиение по одному параметру 56
11.3. Прямые методы оценки качества управления 57
11.3.1. Оценка переходного процесса при ступенчатом воздействии. 57
11.3.2. Оценка качества управления при периодических возмущениях 59
Лекция 12. Корневой и интегральный методы оценки качества САУ 60
12.1. Корневой метод оценки качества управления 60
Лекция 13. Частотные методы оценки качества 65
13.1. Теоретическое обоснование 65
13.2. Основные соотношения между ВЧХ и переходной характеристикой 66
13.3. Метод трапеций 67
Лекция 14. Синтез САУ 70
14.1. Синтез САУ 70
14.1.1. Включение корректирующих устройств 71
14.1.2. Синтез корректирующих устройств. 73
14.2. Коррекция свойств САУ изменением параметров звеньев 73
14.2.2. Изменение постоянной времени звена САУ 75
Лекция 15. Включение корректирующих звеньев 75
15.1. Коррекция свойств САУ включением последовательных корректирующих звеньев 75
15.1.1. Включение интегрирующего звена в статическую САУ 76
15.1.2. Включение апериодического звена 76
15.1.4. Включение звена со сложной передаточной функцией 78
15.2. Последовательная коррекция по задающему воздействию 79
15.3. Коррекция с использованием неединичной обратной связи 80
15.4. Компенсация возмущающего воздействия 81
Лекция 1. Принципы управления
1.1. Общие понятия
Теория автоматического управления (ТАУ) появилась во второй половине 19 века сначала как теория регулирования. Широкое применение паровых машин вызвало потребность в регуляторах, то есть в специальных устройствах, поддерживающих устойчивый режим работы паровой машины. Это дало начало научным исследованиям в области управления техническими объектами. Оказалось, что результаты и выводы данной теории могут быть применимы к управлению объектами различной природы с различными принципами действия. В настоящее время сфера ее влияния расширилась на анализ динамики таких систем, как экономические, социальные и т.п. Поэтому прежнее название “Теория автоматического регулирования” заменено на более широкое - “Теория автоматического управления”.
Управление каким-либо объектом (объект управления будем обозначать ОУ) есть воздействие на него в целях достижения требуемых состояний или процессов. В качестве ОУ может служить самолет, станок, электродвигатель и т.п. Управление объектом с помощью технических средств без участия человека называется автоматическим управлением. Совокупность ОУ и средств автоматического управления называется системой автоматического управления (САУ).
Основной задачей автоматического управления является поддержание определенного закона изменения одной или нескольких физических величин, характеризующих процессы, протекающие в ОУ, без непосредственного участия человека. Эти величины называются управляемыми величинами. Если в качестве ОУ рассматривается хлебопекарная печь, то управляемой величиной будет температура, которая должна изменяться по заданной программе в соответствии с требованиями технологического процесса.
1.2. Фундаментальные принципы управления
Принято различать три фундаментальных принципа управления: принцип разомкнутого управления, принцип компенсации, принцип обратной связи.
1.2.1. Принцип разомкнутого управления
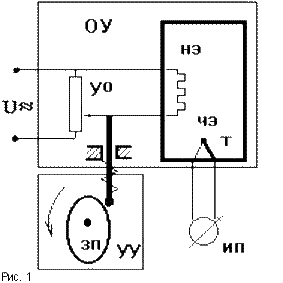
Рассмотрим САУ хлебопекарной печи (рис.1). Ее принципиальная схема показывает принцип действия данной конкретной САУ, состоящей из конкретных технических устройств. Принципиальные схемы могут быть электрическими, гидравлическими, кинематическими и т.п.
Технология выпечки требует изменения температуры в печи по заданной программе, в частном случае требуется поддержание постоянной температуры. Для этого надо реостатом регулировать напряжение на нагревательном элементе НЭ. Подобная часть ОУ, с помощью которой можно изменять параметры управляемого процесса называется управляющим органом объекта (УО). Это может быть реостат, вентиль, заслонка и т.п.
Часть ОУ, которая преобразует управляемую величину в пропорциональную ей величину, удобную для использования в САУ, называют чувствительным элементом (ЧЭ). Физическую величину на выходе ЧЭ называют выходной величиной ОУ. Как правило, это электрический сигнал (ток, напряжение) или механическое перемещение. В качестве ЧЭ могут использоваться термопары, тахометры, рычаги, электрические мосты, датчики давления, деформации, положения и т.п. В нашем случае это термопара, на выходе которой формируется напряжение, пропорциональное температуре в печи, подаваемое на измерительный прибор ИП для контроля. Физическую величину на входе управляющего органа ОУ называют входной величиной ОУ.
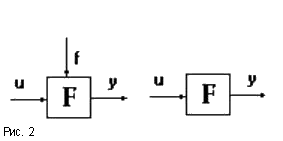
Управляющее воздействие u(t) - это воздействие, прикладываемое к УО объекта с целью поддержания требуемых значений управляемой величины. Оно формируется устройством управления (УУ). Ядром УУ является исполнительный элемент, в качестве которого может использоваться электрические или поршневые двигатели, мембраны, электромагниты и т.п.
Задающим устройством (ЗУ) называется устройство, задающее программу изменения управляющего воздействия, то есть формирующее задающий сигнал uо(t). В простейшем случае uо(t)=const. ЗУ может быть выполнено в виде отдельного устройства, быть встроенным в УУ или же вообще отсутствовать. В качестве ЗУ может выступать кулачковый механизм, магнитофонная лента, маятник в часах, задающий профиль и т.п. Роль УУ и ЗУ может исполнять человек. Однако это уже не САУ. В нашем примере УУ является кулачковый механизм, перемещающий движок реостата согласно программе, которая задается профилем кулачка.
Рассмотренную САУ можно представить в виде функциональной схемы, элементы которой называются функциональными звеньями. Эти звенья изображаются прямоугольниками, в которых записывается функция преобразования входной величины в выходную (рис.2). Эти величины могут иметь одинаковую или различную природу, например, входное и выходное электрическое напряжение, или электрическое напряжение на входе и скорость механического перемещения на выходе и т.п.
Величина f(t), подаваемая на второй вход звена, называется возмущением. Она отражает влияние на выходную величину y(t) изменений окружающей среды, нагрузки и т.п.
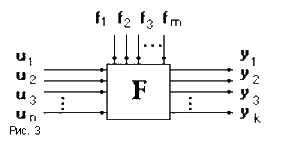
В общем случае функциональное звено может иметь несколько входов и выходов (рис.3). Здесь u1,u2,...,un - входные (управляющие) воздействия; f1,f2,...,fm - возмущающие воздействия; y1,y2,...,yk - выходные величины.
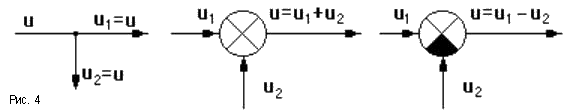
Принцип работы функциональных звеньев может быть различным, поэтому функциональная схема не дает представление о принципе действия конкретной САУ, а показывает лишь пути прохождения и способы обработки и преобразования сигналов. Сигнал - это информационное понятие, соответствующее на принципиальной схеме физическим величинам. Пути его прохождения указываются направленными отрезками (рис.4). Точки разветвления сигнала называются узлами. Сигнал определяется лишь формой изменения физической величины, он не имеет ни массы, ни энергии, поэтому в узлах он не делится, и по всем путям от узла идут одинаковые сигналы, равные сигналу, входящему в узел. Суммирование сигналов осуществляется в сумматоре, вычитание - в сравнивающем устройстве.
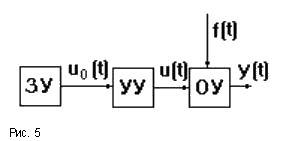
Рассмотренную САУ хлебопекарной печи можно изобразить функциональной схемой (рис.5). В данной схеме заложен принцип разомкнутого управления, сущность которого состоит в том, что программа управления жестко задана ЗУ; управление не учитывает влияние возмущений на параметры процесса. Примерами систем, работающих по принципу разомкнутого управления, являются часы, магнитофон, компьютер и т.п.
1.2.2. Принцип компенсации
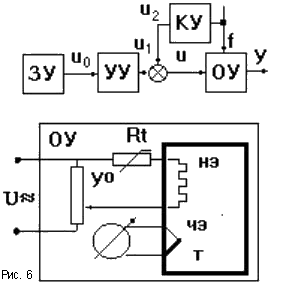
Если возмущающий фактор искажает выходную величину до недопустимых пределов, то применяют принцип компенсации (рис.6, КУ - корректирующее устройство).
Пусть yо - значение выходной величины, которое требуется обеспечить согласно программе. На самом деле из-за возмущения f на выходе регистрируется значение y. Величина e = yо - y называется отклонением от заданной величины. Если каким-то образом удается измерить величину f, то можно откорректировать управляющее воздействие u на входе ОУ, суммируя сигнал УУ с корректирующим воздействием, пропорциональным возмущению f и компенсирующим его влияние.
Примеры систем компенсации: биметаллический маятник в часах, компенсационная обмотка машины постоянного тока и т.п. На рис.6 в цепи НЭ стоит термосопротивление Rt, величина которого меняется в зависимости от колебаний температуры окружающей среды, корректируя напряжение на НЭ.
Достоинство принципа компенсации: быстрота реакции на возмущения. Он более точен, чем принцип разомкнутого управления. Недостаток: невозможность учета подобным образом всех возможных возмущений.
1.2.3. Принцип обратной связи
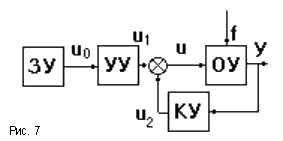
Наибольшее распространение в технике получил принцип обратной связи (рис.7). Здесь управляющее воздействие корректируется в зависимости от выходной величины y(t). И уже не важно, какие возмущения действуют на ОУ. Если значение y(t) отклоняется от требуемого, то происходит корректировка сигнала u(t) с целью уменьшения данного отклонения. Связь выхода ОУ с его входом называется главной обратной связью (ОС).
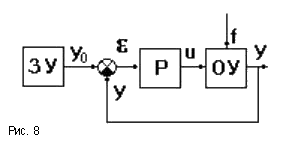
В частном случае (рис.8) ЗУ формирует требуемое значение выходной величины yо(t), которое сравнивается с действительным значением на выходе САУ y(t). Отклонение e = yо-y с выхода сравнивающего устройства подается на вход регулятора Р, объединяющего в себе УУ, УО, ЧЭ.Если e 0, то регулятор формирует управляющее воздействие u(t), действующее до тех пор, пока не обеспечится равенство e = 0

