Файл: Лекция Принципы управления 2 Общие понятия 2 Лекция Статический режим сау 7.doc
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 02.05.2024
Просмотров: 165
Скачиваний: 0
СОДЕРЖАНИЕ
Лекция 2. Статический режим САУ
Лекция 3. Динамический режим САУ
3.1. Динамический режим САУ. Уравнение динамики
Лекция 4.Структурные схемы САУ
4.1. Эквивалентные преобразования структурных схем
4.2. САР напряжения генератора постоянного тока
Лекция 5.Временные характеристики
5.1. Понятие временных характеристик
5.2. Переходные характеристики элементарных звеньев
Лекция 6. Частотные характеристики
6.2. Частотные характеристики типовых звеньев
7.1. Частотные характеристики разомкнутых одноконтурных САУ
Лекция 8. Алгебраические критерии устойчивости
8.1. Понятие устойчивости системы
8.2. Алгебраические критерии устойчивости
Лекция 9. Частотные критерии устойчивости
9.2. Критерий устойчивости Михайлова
9.3. Критерий устойчивости Найквиста
Лекция 10.D-разбиение. Запас устойчивости
10.1. Понятие структурной устойчивости. АФЧХ астатических САУ
10.2. Понятие запаса устойчивости
10.3. Анализ устойчивости по ЛЧХ
11.1. Теоретическое обоснование метода D-разбиений
11.2. D-разбиение по одному параметру
11.3. Прямые методы оценки качества управления
Лекция 13. Частотные методы оценки качества
13.1. Теоретическое обоснование
13.2. Основные соотношения между ВЧХ и переходной характеристикой
14.2. Коррекция свойств САУ изменением параметров звеньев
Лекция 15. Включение корректирующих звеньев
15.1. Коррекция свойств САУ включением последовательных корректирующих звеньев
15.1.1. Включение интегрирующего звена в статическую САУ
15.2. Последовательная коррекция по задающему воздействию
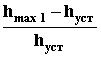 . Здесь hmax1 - значение первого максимума переходной характеристики. При больших перерегулированиях могут возникнуть значительные динамические усилия в механической части системы, электрические перенапряжения и т.п. Допустимое значение s определяется из опыта эксплуатации. обычно оно составляет 0.1...0.3, иногда допускается до 0.7.
. Здесь hmax1 - значение первого максимума переходной характеристики. При больших перерегулированиях могут возникнуть значительные динамические усилия в механической части системы, электрические перенапряжения и т.п. Допустимое значение s определяется из опыта эксплуатации. обычно оно составляет 0.1...0.3, иногда допускается до 0.7.4. Частота колебаний = 2 /T, где T - период колебаний.
5. Число колебаний n за время tпп.
6. Декремент затухания k, равный отношению двух смежных перерегулирований:
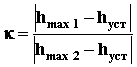 .
.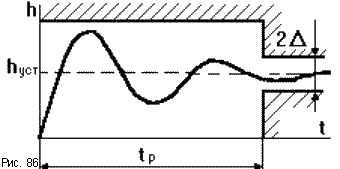
При создании САУ допустимые значения показателей качества оговариваются техническими условиями, что можно представить в виде диаграммы показателей качества. Это область, за границы которой не должна выходить переходная характеристика (рис.86).
11.3.2. Оценка качества управления при периодических возмущениях
Периодические возмущения можно разложить в ряд Фурье, поэтому их воздействие удобно анализировать по частотным характеристикам, показывающим, как звено преобразует гармонический сигнал.
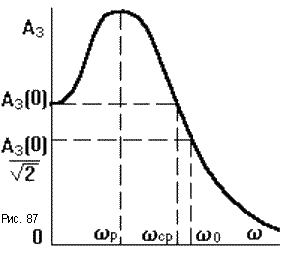
Обычно используют АЧХ замкнутой САУ (рис.87), которую легко построить по АФЧХ разомкнутой САУ Wp(j ), по формуле
Aз =
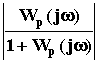 .
. По этой кривой можно получить ряд показателей качества.
1. Показатель колебательности M - это отношение максимального значения АЧХ замкнутой САУ к ее значению при = 0, то есть M = Aзmax( )/Aз(0). Так как
Aз(0) =
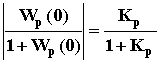 1,
1, при Kp >> 1, то M Aзmax
( ). Он характеризует склонность системы к колебаниям и не должен превышать 1.5.
2. Резонансная частота системы p - это частота, при которой колебания проходят через систему с наибольшим усилением, а АЧХ достигает максимума.
3. Полоса пропускания системы - это интервал частот от = 0 до = 0, на котором выполняется условие Aз( 0) 0.707. Если она высокая, то система будет воспроизводить высокочастотные помехи.
4. Частота среза ср - при которой АЧХ замкнутой САУ принимает значение, равное единице. По ней можно судить о длительности переходного процесса tпп (1..2)2 / ср.
5. Склонность САУ к колебаниям характеризуют также ее запасы устойчивости по модулю (допускается от 6 до 20дб) и по фазе (допускается от 30 до 60 градусов).
Лекция 12. Корневой и интегральный методы оценки качества САУ
12.1. Корневой метод оценки качества управления
Это косвенный метод, основанный на определении границ области расположения корней характеристического уравнения на комплексной плоскости, что дает возможность приблизительно оценить качество управления.
Пусть имеется дифференциальное уравнение замкнутой САУ:
(a0pn + a1pn-1 + a2pn-2 + ... + (an)y = (b0pm + b1pm-1 + ... + bm)u.
Передаточная функция САУ
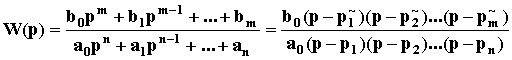 ,
,
где p
1,p
2,...,p
m - нули передаточной функции, p1,p2,...,pn - полюса передаточной функции.
Лекция 12. Корневой и интегральный методы оценки качества САУ
12.1. Корневой метод оценки качества управления
Это косвенный метод, основанный на определении границ области расположения корней характеристического уравнения на комплексной плоскости, что дает возможность приблизительно оценить качество управления.
Пусть имеется дифференциальное уравнение замкнутой САУ:
(a0pn + a1pn-1 + a2pn-2 + ... + (an)y = (b0pm + b1pm-1 + ... + bm)u.
Передаточная функция САУ
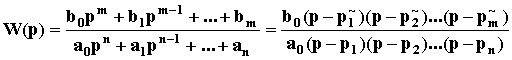 ,
,
где p
1,p
Лекция 12. Корневой и интегральный методы оценки качества САУ
 Переходный процесс зависит как от полюсов, так и от нулей, то есть определяется как левой, так и правой частями дифференциального уравнения. Это существенно усложняет анализ. Поэтому рассмотрим частный, но весьма распространенный случай, когда передаточная функция замкнутой САУ не имеет нулей:
Переходный процесс зависит как от полюсов, так и от нулей, то есть определяется как левой, так и правой частями дифференциального уравнения. Это существенно усложняет анализ. Поэтому рассмотрим частный, но весьма распространенный случай, когда передаточная функция замкнутой САУ не имеет нулей: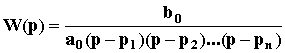 .
. Тогда уравнение динамики приобретает вид:
(a0pn + a1pn-1 + a2pn-2 + ... + an)y = b0u.
Общее решение данного уравнения имеет вид:
y(t) = yсв + yвын = åAiepit + bо/an.
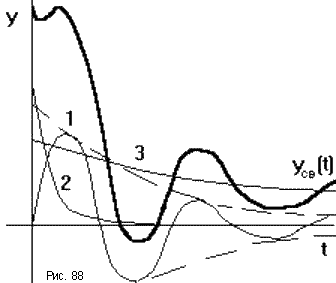
Время переходного процесса tпп определяется длительностью свободного процесса, который представляет собой сумму n экспоненциально затухающих составляющих (рис.88). Затухание каждой из составляющих определяется вещественной частью соответствующего плюса pi, которая для устойчивых систем должна быть отрицательна. Длительность переходного процесса определяется в основном свободной составляющей
, имеющей наименьшее затухание, то есть наименьшее абсолютное значение вещественной части соответствующего полюса.
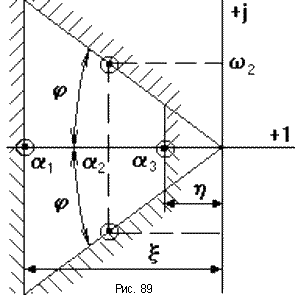
Если изобразить все полюса в комплексной плоскости корней (рис.89), то данный полюс (или пара комплексно сопряженных полюсов) будет наиболее близко расположен к мнимой оси.
Для приблизительной оценки качества САУ на плоскости корней выделяется область в виде трапеции, на сторонах которой находится хотя бы по одному корню, все остальные корни - внутри данной области. Эта область характеризуется параметрами: h - степень устойчивости (равна расстоянию от мнимой оси до ближайшего корня или пары комплексно сопряженных корней); m = tg(j) - колебательность (характеризует колебательность переходного процесса и величину перерегулирования); x - своего названия не имеет, равна вещественной части наиболее удаленного от мнимой оси корня.
По степени устойчивости h можно приблизительно вычислить время переходного процесса, которое определяется по моменту, когда свободная составляющая с наименьшим затуханием уменьшится до величины Ai , где Ai - начальное значение данной составляющей, то на рис.84:
yсв3(t) = A3 = A3 = >
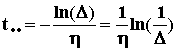 .
.В общем случае, когда передаточная функция замкнутой САУ имеет нули, то использование данного метода может дать большую ошибку. Однако всегда качество управления будет тем лучше, чем больше h и меньше m, поэтому данный метод имеет смысл для любых САУ, но приближенно.
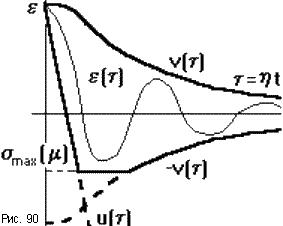
Зная значения h, x, m можно оценить область, за которую кривая переходного процесса выходить не будет (рис.90). Для этого строятся две кривые: u(t,h) - миноранта и v(t,h) - мажоранта, ограничивающая кривую переходного процесса соответственно снизу и сверху так, что u(t,h) e(t) v(t,h), где e(t) = yo-y(t). Формулы для определения миноранты и мажоранты берутся в справочниках для конкретных случаев.
12.2. Интегральные критерии качества
Интегральные критерии позволяют судить о качестве управления путем вычисления интегралов от некоторых функций управляемой величины. Эта функция выбирается таким путем, чтобы значение определенного интеграла от этой функции по времени от
0 до + было однозначно связано с качеством переходного процесса. В то же время данный интеграл должен сравнительно просто вычисляться через коэффициенты уравнений исследуемой системы.

Например, если переходная характеристика является монотонной, то можно утверждать, что качество переходного процесса тем лучше, чем меньше площадь, ограниченная данной кривой и установившимся значением управляемой величины (рис.91). Она равна площади, ограниченной кривой изменения свободной составляющей управляемой величины и осью абсцисс.
Если система устойчива, то свободная составляющая управляемой величины в пределе стремится к нулю , поэтому площадь ограниченная данной кривой имеет конечное значение и определяется по формуле:
Joo =
Величина Joo представляет собой линейную оценку качества управления.
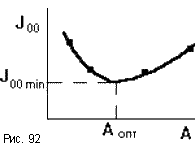
Чем она меньше, тем выше быстродействие системы. При выборе параметров системы стремятся обеспечить минимум Joo. Если имеется какой то варьируемы параметр A, то можно построить кривую Joo = f(A) (рис.92). Ее минимум, определяемый из условия dJoo/dA = 0, даст оптимальное значение A.
Пусть дано уравнение динамики замкнутой САУ:
(a0pn + a1pn-1 + a2pn-2 + ... + an)y = (b0pm + b1pm-1 + ... + bm)u.
Свободный процесс описывается однородным дифференциальным уравнением:
(a0pn + a1pn-1 + ... + an)yсв = 0,
следовательно:
yсв =
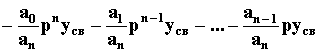
yсв =
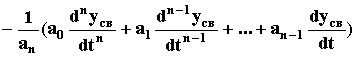
Joo = св(t)dt =
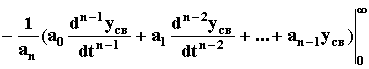 .
.Пусть при t = 0 САУ имела следующие начальные условия:

