Файл: Курсовая работа по курсу Разработки и проектирование нефтяных месторождений.docx

3. 
   Определяют значения фазовых проницаемостей по воде К_в и нефти К_н при различных фиксированных значениях текущей водонасыщенности S_i согласно уравнению
   

4. 
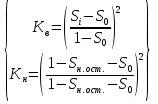
   Определяют функцию Баклея-Леверетта:
   

5. 
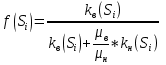
   Определяют дифференциал от функции Баклея-Леверетта:
   

6. 
   Строят график зависимости функции Баклея-Леверетта f(S_i) от текущей водонасыщенности S_i. Пример графика представлен на рисунке 3.2.
   
7. 
   На графике проводят касательную линию от S₀ к зависимости f(S_i)=F(S_i) и определяют значения S_ф и f(S_ф), где S_ф – водонасыщенность на фронте вытеснения нефти водой, f(S_ф) – значение функции Баклея-Леверетта на фронте вытеснения нефти водой.
   
8. 
   Определяют дифференциал функции Баклея Леверетта, соответствующий водонасыщенности на фронте вытеснения нефти водой:
   

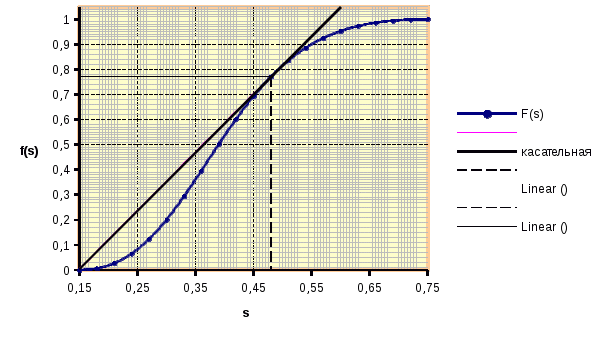
Рисунок 3.2 – Зависимость функции Баклея-Леверетта от водонасыщенности

9. 
   Определяют время безводной эксплуатации добывающей скважины:
   

9. 
   Определяют водный период разработки залежи. Предполагают, что при t>t⁰ фронт вытеснения нефти водой существует как фиктивный, т.е. кажущийся фронт вытеснения при r>R_к. Исходя из этого предположения, получено соотношение для добычи продукции скважины за водный период времени:
   

где – кажущаяся водонасыщенность за пределами элемента залежи.

9. 
   Строят график зависимости дифференциала функции Баклея-Леверетта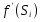 от текущей водонасыщенности S_i. Пример графика представлен на рисунке 3.3
   

---

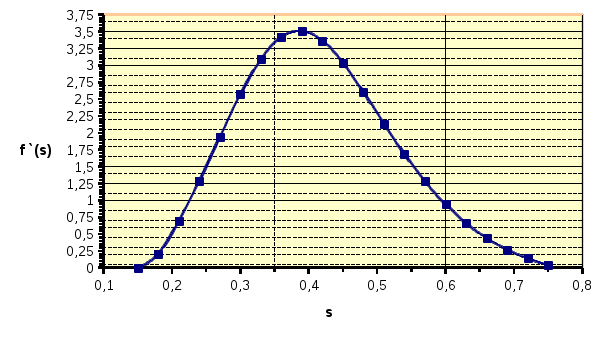
Рисунок 3.3 – Зависимость дифференциала функции Баклея-Леверетта от водонасыщенности

9. 
   Задаются временным интервалом разработки элемента залежи за водный период эксплуатации: 1 год.
   
10. 
    По формуле (1) Определяют дифференциал функции Баклея-Леверетта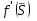 за водный период разработки элемента залежи.
    
11. 
    По графику 2 Определяют кажущуюся водонасыщенность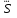 за водный период разработки элемента залежи по годам разработки.
    
12. 
    По графику 1 определяют функцию Баклея-Леверетта f(S) от кажущейся водонасыщенности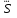 за водный период разработки элемента залежи по годам разработки. Полученная функция Баклея-Леверетта соответствует обводненности продукции скважины за водный период разработки элемента залежи:
    

13. 
    Определяют суточную добычу воды за водный период эксплуатации по годам разработки:
    

14. 
    Определяют суточную добычу нефти за водный период эксплуатации по годам разработки:
    

15. 
    Определяют годовую добычу воды за водный период эксплуатации по годам разработки:
    

16. 
    Определяют годовую добычу нефти за водный период эксплуатации по годам разработки:
    

Все расчеты ведут до обводненности n_в =98 %.

17. 
    Определяют геологические запасы нефти элемента залежи:
    

18. 
    Определяют накопленную добычу нефти из элемента залежи (до обводненности продукции 95 %):
    

19. 
    Определяют текущий коэффициент нефтеотдачи элемента залежи по годам разработки:
    

---

20. 
    Строят график динамики показателей разработки элемента залежи. Пример графика представлен на рисунке 3.3.
    

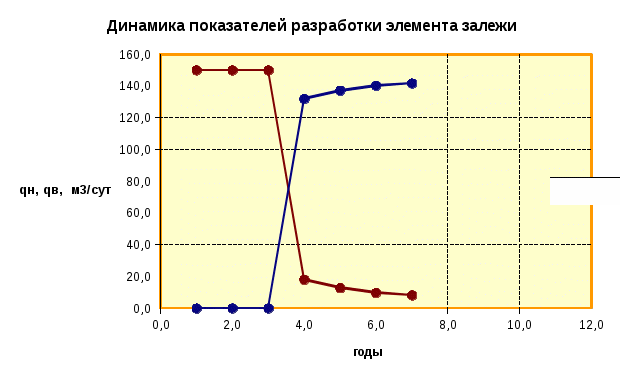
Рисунок 3.4 – Динамика показателей разработки элемента залежи

21. 
    Определяют динамику добычи нефти по всему месторождению, с учетом того, что оно вводится в разработку в течение 10 лет. Определяют динамику добычи воды по всему месторождению с учетом того, что оно вводится в разработку в течение 10 лет.
    
22. 
    Определяют годовую добычу жидкости по всему месторождению.
    

23. 
    Определяют обводненность добываемой жидкости по годам разработки:
    

24. 
    Определяют годовой водонефтяной фактор:
    

25. 
    Определяют накопленную добычу нефти по всему месторождению по годам разработки:
    

26. 
    Определяют накопленную добычу воды по всему месторождению по годам разработки:
    

27. 
    Определяют накопленный водонефтяной фактор
    

28. 
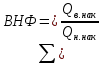
    Определяют геологические запасы нефти всего месторождения:
    

29. 
    Определяют коэффициент нефтеотдачи по годам разработки по всему месторождению:
    

Все расчеты по пунктам 26-33 сводят таблицу

---

3.2 Метод М.М. Саттарова

Данный метод основан на теории поршневого вытеснения, учитывает объёмную неоднородность пластов.

Все пласты неоднородны по проницаемости. Если рассматривать проницаемость как случайную величину, то для расчёта процесса обводнения можно использовать теорию вероятности. Знать проницаемость в каждой точке, мы не имеем возможности, но мы можем найти закон распределения проницаемости по объёму пласта. Саттаров предложил заменить реальный пласт моделью, состоящей из трубок тока различной проницаемости. Изменение проницаемости трубок подчиняется закону распределения Саттарова. Проницаемость каждой трубки тока постоянны по её длине. Трубки отделены друг от друга перегородками бесконечно малой толщины, следовательно перетоков между трубками тока нет. Вытеснение поршневое, скорость вытеснения нефти водой пропорциональна проницаемости трубок тока.

Допустим, в какой-то момент времени t по какой-то трубке тока с проницаемостью К_m в скважину подошла вода. По всем трубкам, у которых К K_m поступает вода, у которых К<К_m поступает нефть.

Количество нефти и воды поступающей в момент времени t в галерею определяются по следующим формулам:
, (3.1)

, (3.2)
где К_Н и К_В – средние абсолютные проницаемости трубок тока, по которым поступает нефть или вода.

Количество жидкости определим как сумму нефти и воды:
q_Ж=q_Н+q_В, (3.3)
Долю нефти найдём как отношение количества нефти к количеству жидкости:

f_н=q_н/q_ж, (3.4)

Подставив значения, в конечном итоге получим:

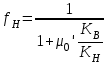, (3.5)
где – подвижность воды.

Зная долю нефти, мы можем найти долю воды:
, (3.6)
Средняя проницаемость трубок тока, по которым поступает вода в данный момент времени изменяется от бесконечности до К_m, по которым поступает нефть средняя проницаемость изменяется от К

---

_m до 0. Проницаемости трубок тока как нефтяной так и обводнённой части изменяются согласно закону Саттарова:
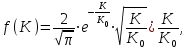(3.7)

, (3.8)

, (3.9)

Подставив 3.7 в 3.8 и 3.9 и интегрируя полученные выражения по частям, получим:

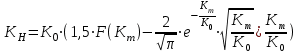, (3.10)

где ,

(3.11)
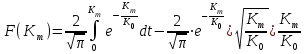Таким образом, мы можем вычислить для любого значения проницаемости количество поступающей нефти и воды, а следовательно долю нефти и воды в добываемой продукции.

В дальнейшем необходимо увязать обводнённость продукции со временем, найти связь между К_m и t. Пользоваться временем в явном виде для расчёта показателей разработки достаточно неудобно, для упрощения расчётов и увязывания времени непосредственно с показателями разработки введём понятие безразмерного времени:

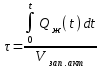, (3.12)
где V_{зап.акт.}= - активные запасы; Q_ж(t) – годовая добыча жидкости.

Годовая добыча равна сумме годовых объемов добычи нефти и воды:
;
Найдем безразмерное время, подставив в (3.12) последнее выражение:

, (3.13)
Как видно из формул как f_Н так и τ зависят от параметра K_m, поэтому должна существовать связь и между f_Н и τ. Типичный график зависимости представлен на рисунке 3.5.



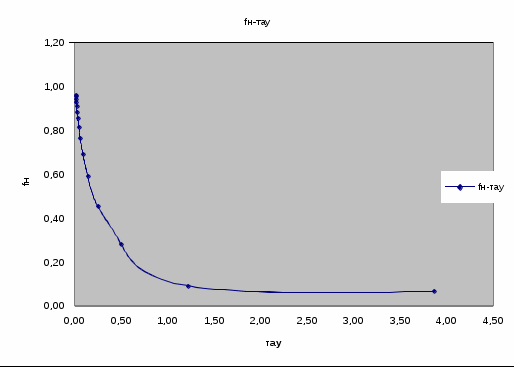
Рисунок 3.5 – График зависимости доли нефти от безразмерного времени
Далее переходят к расчету средних дебитов рядов и скважин.

Для определения средних дебитов рядов и скважин используют приведенный радиус питания – воображаемую линию, в общем случае не совпадающую с реальным контуром питания, где давление принимается равным давлению на реальном контуре питания, а вязкость вытесняющего агента принимается равной вязкости вытеснения. Если вязкость воды меньше вязкости нефти, то приведенный контур питания находится ближе к добывающим рядам, чем реальный контур питания и наоборот. Расчет средних дебитов осуществляется, используя уравнение интерференции по методу Ю.П. Борисова. Так как свойства пород одинаковы в соответствующих областях реальной залежи и модели, для нахождения фактического значения третьего ряда необходимо расчетный дебит поделить на фактическое количество скважин, имеющихся на реальной залежи.

---