Файл: Курсовая работа по курсу Разработки и проектирование нефтяных месторождений.docx
Добавлен: 16.03.2024
Просмотров: 110
Скачиваний: 2
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
– дебит по воде i-того добывающего ряда.
Далее определяют накопленную добычу нефти, воды, жидкости и строят график изменения их во времени
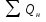 =
= 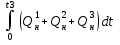 – накопленная добыча нефти; (3.25)
– накопленная добыча нефти; (3.25)
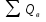 =
=  – накопленная добыча воды; (3.26)
– накопленная добыча воды; (3.26)
 =
= 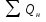 +
+ 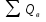 – накопленная добыча жидкости.
– накопленная добыча жидкости.
Находится коэффициент нефтеотдачи пласта по следующей формуле:
Ƞ =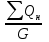 , (3.27)
, (3.27)
где Ƞ – коэффициент нефтеодачи пласта (КНО);
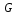 – балансовые запасы нефти на всей залежи.
– балансовые запасы нефти на всей залежи.
Определив конечных коэффициент нефтеотдачи строят графики изменения текущего коэффициента нефтеотдачи и обводнённости во времени
Затем рассчитываем текущий водонефтяной фактор по следующей формуле:
W =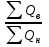 , (3.28)
, (3.28)
где W – водонефтяной фактор (ВНФ).
Строят график изменения водонефтяного фактора во времени
Наконец, определив все намеченные показатели разработки, результаты которых сводятся также в таблицы, строят графики изменения обводненности по рядам, годовой и накопленной добычи по рядам, а также годовой и накопленной добычи по всей залежи во времени для жидкости, воды и нефти.
Порядок расчета показателей разработки:
1. Рассчитывают площадь залежи
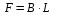 м2,
м2,
где В - ширина залежи, м; L - длина залежи, м.
2. Находят начальные балансовые запасы нефти объёмным методом
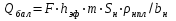 т,
т,
где hэф - эффективная нефтенасыщенная мощность, м; m - коэффициент пористости, доли ед.; Sн - коэффициент нефтенасыщенности, доли ед.; rнпл - плотность нефти в пластовых условиях, т/м3; bн - объёмный коэффициент нефти, доли ед.
3. В случае L/B>1,5 данную залежь схематизируем как полосообразную. Для неё используют трёхрядное размещение добывающих скважин с законтурным заводнением. Если залежь с двусторонним питанием делим её на две равные части и проводят расчёты только для одной.
3.1. Определяют среднее расстояние между рядами
 м,
м,
где n - число рядов.
3.2. Определяют расстояние от контура питания до первого добывающего ряда и между первым и вторым рядами соответственно по формулам
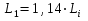 м,
м,
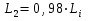 м.
м.
3.3. Находят
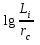 ,
,
где rc - приведённый радиус скважины, м.
3.4. По номограмме из книги [6] находят среднее расстояние между скважинами
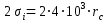 м.
м.
3.5. Рассчитывают среднее количество скважин
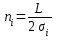 .
.
3.6. Определяют количество скважин в рядах
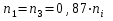 скв,
скв,
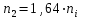
скв.
3.7. Находят расстояния между скважинами в рядах
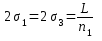 м,
м,
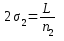 м.
м.
4. Рассчитывают параметр Крылова
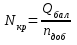 т/скв.
т/скв.
5. Определяют дебиты в рядах по формуле Маскета

 ,
,
 ,
,
где k - проницаемость, м2; - динамическая вязкость нефти, Па*с; Р=3 МПа - перепад давления, Па; н - плотность нефти в поверхностных условиях, т/м3; Rк1, Rк2 - расстояние до контура питания, м.
7. Находят приращение величины безразмерного времени
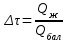 .
.
8. Исходя из соотношения вязкостей нефти и воды, выбирают модель слоисто-неоднородного пласта и адаптируют на рассматриваемые условия условия. Результаты расчетов показателей разработки по выше приведенным формулам заносят в таблицу
Исходные данные гипотетической залежи
Нефтяное месторождение площадью нефтеносности S=3600∙104 м2 разрабатывается с использованием заводнения при однорядной схеме расположения скважин. Элемент однорядной схемы, содержащий одну скважину (1/2 добывающей и 1/2 нагнетательной), имеет ширину b = 600 м и длину 1 = 600 м. Месторождение вводится в разработку за 10 лет, причем во времени месторождение разбуривается равномерно. Разрабатываемый пласт месторождения имеет следующие параметры: толщина h = 20 м; коэффициент пористости m = 0,22; начальная водонасыщенность связанной водой Scв=S0 =0,25; вязкость нефти в пластовых условиях μн= 7 мПас; вязкость воды в пластовых условиях μв = 1,3 мПас; коэффициент охвата заводнением по толщине пласта К
охв = 0,75. Остаточная нефтенасыщенность Sн.ост=0,29 [1].
Расчетная часть
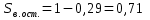
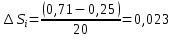
Таблица 4.1 - Зависимость функции Баклея-Леверетта и дифференциала функции Баклея-Леверетта от текущей водонасыщенности
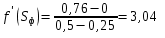
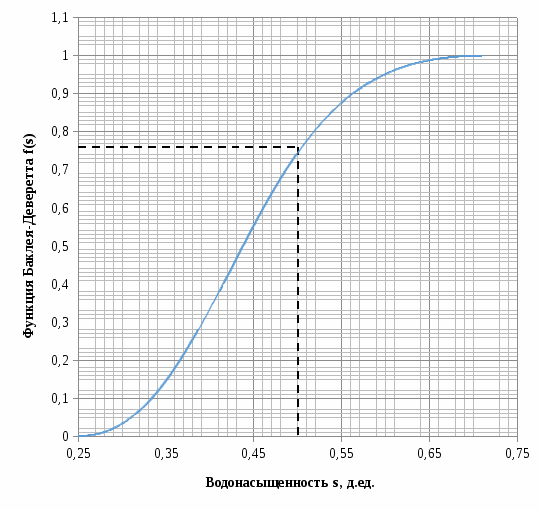
Рисунок 4.1 – Зависимость функции Баклея-Леверетта от водонасыщенности

где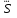 – кажущаяся водонасыщенность за пределами элемента залежи.
– кажущаяся водонасыщенность за пределами элемента залежи.
Далее определяют накопленную добычу нефти, воды, жидкости и строят график изменения их во времени
Находится коэффициент нефтеотдачи пласта по следующей формуле:
Ƞ =
где Ƞ – коэффициент нефтеодачи пласта (КНО);
Определив конечных коэффициент нефтеотдачи строят графики изменения текущего коэффициента нефтеотдачи и обводнённости во времени
Затем рассчитываем текущий водонефтяной фактор по следующей формуле:
W =
где W – водонефтяной фактор (ВНФ).
Строят график изменения водонефтяного фактора во времени
Наконец, определив все намеченные показатели разработки, результаты которых сводятся также в таблицы, строят графики изменения обводненности по рядам, годовой и накопленной добычи по рядам, а также годовой и накопленной добычи по всей залежи во времени для жидкости, воды и нефти.
3.3 Метод ГипроВостокнефть
Порядок расчета показателей разработки:
1. Рассчитывают площадь залежи
где В - ширина залежи, м; L - длина залежи, м.
2. Находят начальные балансовые запасы нефти объёмным методом
где hэф - эффективная нефтенасыщенная мощность, м; m - коэффициент пористости, доли ед.; Sн - коэффициент нефтенасыщенности, доли ед.; rнпл - плотность нефти в пластовых условиях, т/м3; bн - объёмный коэффициент нефти, доли ед.
3. В случае L/B>1,5 данную залежь схематизируем как полосообразную. Для неё используют трёхрядное размещение добывающих скважин с законтурным заводнением. Если залежь с двусторонним питанием делим её на две равные части и проводят расчёты только для одной.
3.1. Определяют среднее расстояние между рядами
где n - число рядов.
3.2. Определяют расстояние от контура питания до первого добывающего ряда и между первым и вторым рядами соответственно по формулам
3.3. Находят
где rc - приведённый радиус скважины, м.
3.4. По номограмме из книги [6] находят среднее расстояние между скважинами
3.5. Рассчитывают среднее количество скважин
3.6. Определяют количество скважин в рядах
скв.
3.7. Находят расстояния между скважинами в рядах
4. Рассчитывают параметр Крылова
5. Определяют дебиты в рядах по формуле Маскета
 ,
,  ,
, где k - проницаемость, м2; - динамическая вязкость нефти, Па*с; Р=3 МПа - перепад давления, Па; н - плотность нефти в поверхностных условиях, т/м3; Rк1, Rк2 - расстояние до контура питания, м.
7. Находят приращение величины безразмерного времени
8. Исходя из соотношения вязкостей нефти и воды, выбирают модель слоисто-неоднородного пласта и адаптируют на рассматриваемые условия условия. Результаты расчетов показателей разработки по выше приведенным формулам заносят в таблицу
4 Расчет показателей разработки гипотетической залежи методом Баклея-Леверетта
Исходные данные гипотетической залежи
Нефтяное месторождение площадью нефтеносности S=3600∙104 м2 разрабатывается с использованием заводнения при однорядной схеме расположения скважин. Элемент однорядной схемы, содержащий одну скважину (1/2 добывающей и 1/2 нагнетательной), имеет ширину b = 600 м и длину 1 = 600 м. Месторождение вводится в разработку за 10 лет, причем во времени месторождение разбуривается равномерно. Разрабатываемый пласт месторождения имеет следующие параметры: толщина h = 20 м; коэффициент пористости m = 0,22; начальная водонасыщенность связанной водой Scв=S0 =0,25; вязкость нефти в пластовых условиях μн= 7 мПас; вязкость воды в пластовых условиях μв = 1,3 мПас; коэффициент охвата заводнением по толщине пласта К
охв = 0,75. Остаточная нефтенасыщенность Sн.ост=0,29 [1].
Расчетная часть
-
Определяем водонасыщенность пласта к моменту завершения процесса разработки:
| | | (1) |
-
Определяем интервал изменения текущей водонасыщенности таким образом, чтобы количество точек на графике не было менее 20.
| | | (2) |
-
Определяем значения фазовых проницаемостей по воде Кв и нефти Кн при различных фиксированных значениях текущей водонасыщенности Si согласно уравнению
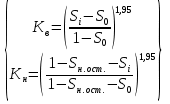
(3)
-
Определяем функцию Баклея-Леверетта:

(4)
-
Определяем дифференциал от функции Баклея-Леверетта:
| |  | (5) |
Таблица 4.1 - Зависимость функции Баклея-Леверетта и дифференциала функции Баклея-Леверетта от текущей водонасыщенности
| s | Кн | Кв | f(s) | f `(s) |
| 0.25 | 1 | 0 | 0 | 0 |
| 0.273 | 0.9048 | 0.0011 | 0.0066 | 0.2877 |
| 0.296 | 0.8143 | 0.0043 | 0.0278 | 0.9212 |
| 0.319 | 0.7284 | 0.0095 | 0.0659 | 1.6543 |
| 0.342 | 0.6472 | 0.0167 | 0.1221 | 2.4441 |
| 0.365 | 0.5706 | 0.0258 | 0.1959 | 4.2109 |
| 0.388 | 0.4988 | 0.0368 | 0.2846 | 4.8541 |
| 0.411 | 0.4317 | 0.0498 | 0.3830 | 4.2799 |
| 0.434 | 0.3693 | 0.0646 | 0.4849 | 4.4310 |
| 0.457 | 0.3117 | 0.0812 | 0.5839 | 4.3057 |
| 0.48 | 0.2588 | 0.0998 | 0.6749 | 4.9533 |
| 0.503 | 0.2107 | 0.1201 | 0.7543 | 4.4529 |
| 0.526 | 0.1675 | 0.1424 | 0.8207 | 2.8866 |
| 0.549 | 0.1291 | 0.1664 | 0.8741 | 2.3213 |
| 0.572 | 0.0956 | 0.1923 | 0.9155 | 1.8007 |
| 0.595 | 0.0670 | 0.2200 | 0.9465 | 1.3474 |
| 0.618 | 0.0434 | 0.2495 | 0.9687 | 0.9679 |
| 0.641 | 0.0247 | 0.2808 | 0.9839 | 0.6593 |
| 0.664 | 0.0112 | 0.3139 | 0.9934 | 0.4132 |
| 0.687 | 0.0029 | 0.3488 | 0.9985 | 0.2196 |
| 0.71 | 0.0000 | 0.3855 | 1.0000 | 0.0671 |
-
Строим график зависимости функции Баклея-Леверетта f(Si) от текущей водонасыщенности Si -
На графике проводим касательную линию от S0 к зависимости f(Si)=F(Si) и определяют значения Sф и f(Sф), где Sф – водонасыщенность на фронте вытеснения нефти водой, f(Sф) – значение функции Баклея-Леверетта на фронте вытеснения нефти водой. Для данного примера Sф = 0,5, f(Sф) = 0,76. -
Определяем дифференциал функции Баклея Леверетта, соответствующий водонасыщенности на фронте вытеснения нефти водой:
| | | (6) |

Рисунок 4.1 – Зависимость функции Баклея-Леверетта от водонасыщенности
-
Определяем время безводной эксплуатации добывающей скважины:
| | | (7) |
-
Определяем водный период разработки залежи. Предполагают, что при t>t0 фронт вытеснения нефти водой существует как фиктивный, т.е. кажущийся фронт вытеснения при r>Rк. Исходя из этого предположения, получено соотношение для добычи продукции скважины за водный период времени:
| | | (8) |
где
| | | (9) |
-
Строим график зависимости дифференциала функции Баклея-Леверетта1 2 3 4 5 6 7
