Добавлен: 17.03.2024
Просмотров: 92
Скачиваний: 0
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Расчёт пусковых характеристик с учётом влияния вытеснения тока и насыщения от полей рассеяния
Расчет проводим для точек характеристик, соответствующих
 , при этом используем значения токов и сопротивлений для тех же скольжений с учетом влияния вытеснения тока.
, при этом используем значения токов и сопротивлений для тех же скольжений с учетом влияния вытеснения тока.Ориентировочно для расчета пусковых режимов принимают
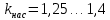 , для режима максимального момента
, для режима максимального момента 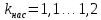 . В нашем случае примем
. В нашем случае примем 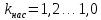 . Для
. Для  принимаем
принимаем 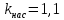 8
861. Индуктивные сопротивления обмоток
Определим среднюю МДС обмотки, отнесенную к одному пазу обмотки статора по формуле:
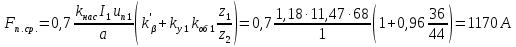
Фиктивная индукция потока рассеяния в воздушном зазоре рассчитывается по средней МДС
 по формуле (41):
по формуле (41):  | (41) |
Здесь коэффициент
 определяется по следующей формуле:
определяется по следующей формуле: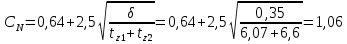
По формуле (41) определяем
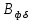 :
: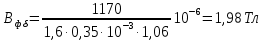
По полученному значению
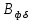 определяем отношение потока рассеяния при насыщении к потоку рассеяния ненасыщенной машины, характеризуемое коэффициентом
определяем отношение потока рассеяния при насыщении к потоку рассеяния ненасыщенной машины, характеризуемое коэффициентом  , значение которого определяется по рисунку 9.61 [2] и составляет:
, значение которого определяется по рисунку 9.61 [2] и составляет:

Коэффициент магнитной проводимости пазового рассеяния обмотки статора с учетом влияния насыщения определяется следующим образом:
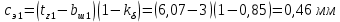
Коэффициент магнитной проводимости пазового рассеяния при насыщении
 определяют для статора по формуле (48):
определяют для статора по формуле (48):  | (48) |
Здесь для полузакрытого паза коэффициент
 определяется по формуле (49):
определяется по формуле (49):  | (49) |
Здесь

По формуле (49) находим:

По формуле (48) находим:

Коэффициент магнитной проводимости дифференциального рассеяния обмотки статора с учетом влияния насыщения определяется следующим образом:
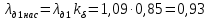
Индуктивное сопротивление обмотки статора с учетом насыщения от полей рассеяния определяют по отношению сумм коэффициентов проводимости, рассчитанных без учета и с учетом насыщения от полей рассеяния по следующей формуле:

Коэффициент магнитной проводимости пазового рассеяния при насыщении
 определяют для ротора по формуле (42):
определяют для ротора по формуле (42):  | (42) |
Здесь уменьшение коэффициента проводимости
 определяется по формуле (43):
определяется по формуле (43): 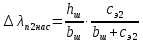 | (43) |
Для короткозамкнутых роторов дополнительное раскрытие
 рассчитывается следующим образом:
рассчитывается следующим образом:
С учетом того, что для закрытых пазов ротора
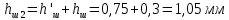 по формуле (43) получаем:
по формуле (43) получаем: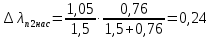
По формуле (42) получаем:

Коэффициенты проводимости дифференциального рассеяния при насыщении участков зубцов ротора
 определяется следующим образом:
определяется следующим образом:
Приведенное индуктивное сопротивление фазы обмотки ротора с учетом влияния эффекта вытеснения тока и насыщения определяется по следующей формуле:

Коэффициент
 определяется по формуле (43):
определяется по формуле (43): 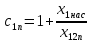 | (43) |
Здесь

По формуле (43) получаем:
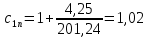
62. Расчет токов и моментов


Ток в обмотке ротора определяется как:


Кратность пускового тока с учетом влияния вытеснения тока и насыщения определяется следующей формулой:
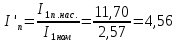
Кратность пускового момента с учетом влияния вытеснения тока и насыщения определяется следующей формулой:

Коэффициент насыщения:

Полученный в расчете коэффициент насыщения отличается от принятого ранее значения
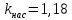
на
 , что входит в диапазон допустимых расхождений (
, что входит в диапазон допустимых расхождений ( ). Следовательно, расчет для
). Следовательно, расчет для  окончен.
окончен.Таблица 3 – Расчет пусковых характеристик асинхронного двигателя с короткозамкнутым ротором с учетом эффекта вытеснения тока и насыщения от полей рассеяния
| № п/п | Расчетная формула | | Скольжение | |||||
| 1 | 0,8 | 0,5 | 0,2 | 0,1 |  | |||
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| 1 |  | - | 1,2 | 1,18 | 1,15 | 1,1 | 1,05 | 1,11 |
| 2 |  |  | 1170 | 1141 | 1111 | 1091 | 1041 | 1101 |
| 3 |  |  | 1,98 | 1,93 | 1,88 | 1,84 | 1,76 | 1,86 |
| 4 | 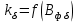 | - | 0,87 | 0,87 | 0,9 | 0,89 | 0,9 | 0,88 |
| 5 |  |  | 0,4 | 0,4 | 0,31 | 0,34 | 0,31 | 0,37 |
| 6 |  | - | 1,050 | 1,051 | 1,057 | 1,055 | 1,056 | 1,053 |
| 7 |  | - | 0,95 | 0,95 | 0,98 | 0,97 | 0,98 | 0,96 |
| 8 |  |  | 4,28 | 4,28 | 4,33 | 4,31 | 4,33 | 4,29 |
| 9 |  | - | 1,0213 | 1,0231 | 1,0215 | 1,0214 | 1,0215 | 1,0213 |
| 10 |  |  | 0,66 | 0,66 | 0,51 | 0,56 | 0,51 | 0,61 |
| 11 |  | - | 5,12 | 5,2 | 5,27 | 5,3 | 5,34 | 5,24 |
| 12 |  | - | 1,15 | 1,17 | 1,22 | 1,20 | 1,22 | 1,19 |
| 13 |  |  | 6,91 | 7,02 | 7,13 | 7,14 | 7,20 | 7,07 |
| 14 |  |  | 15,89 | 17,14 | 22,81 | 37,47 | 63,83 | 21,44 |
| 15 | 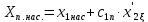 |  | 11,30 | 16,13 | 11,95 | 11,96 | 16,28 | 11,89 |
| 16 | 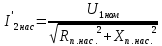 |  | 11,28 | 9,35 | 8,54 | 5,59 | 3,34 | 8,97 |
| 17 |  |  | 11,70 | 9,92 | 8,91 | 5,89 | 3,68 | 9,35 |
| 18 | 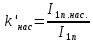 | - | 1,18 | 1,09 | 1,06 | 1,00 | 1,00 | 1,04 |
| 19 |  | - | 4,56 | 3,86 | 3,47 | 2,29 | 1,43 | 3,64 |
| 20 |  | - | 1,66 | 1,40 | 2,14 | 2,00 | 1,41 | 2,10 |
63. Критическое скольжение определяем после расчета всех точек пусковых характеристик по средним значениям сопротивлений
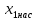 и
и  , соответствующим скольжениям
, соответствующим скольжениям 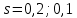 по формуле (44):
по формуле (44): 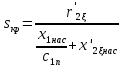 | (44) |
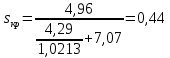
После расчета всей пучковой характеристики можно сделать вывод, что значение
 , а
, а  .
.На рисунке 4 представлены пусковые характеристики спроектированного двигателя с короткозамкнутым ротором.
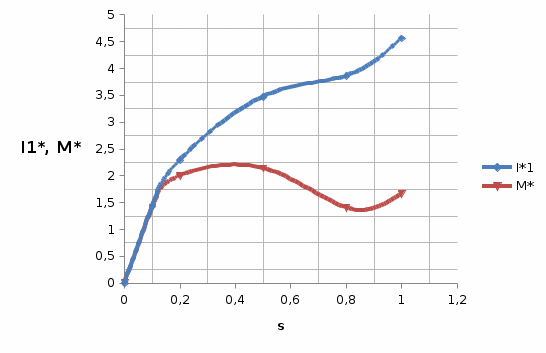 |
| Рисунок 4 – Пусковые характеристики спроектированного двигателя с короткозамкнутым ротором |
