Добавлен: 17.03.2024
Просмотров: 88
Скачиваний: 0
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Для расчета
 используются найденные ранее значения:
используются найденные ранее значения: (из п. Error: Reference source not found),
(из п. Error: Reference source not found),  (из п. 0),
(из п. 0), 
По формуле (20) получаем:

По формуле (19) находим:
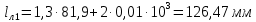
По формуле (18) определим среднюю длину витка обмотки:

Вылет лобовых частей обмотки определяется по формуле (с учетом табличного коэффициента
 ):
):
Далее определим общую длину проводников фазы обмотки по формуле (19):

По формуле (18) с учетом
 (для нормальных машин) и
(для нормальных машин) и 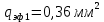 (из п. 16) находим:
(из п. 16) находим: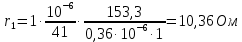
Относительное значение
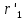 определяется по формуле:
определяется по формуле: 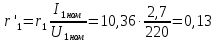
45. Активное сопротивление фазы алюминиевой обмотки ротора определяется по формуле (21):
 | (21) |
Где
 определяется по формуле (22),
определяется по формуле (22),  - по формуле (23) и, учитывая, что для литой алюминиевой обмотки ротора
- по формуле (23) и, учитывая, что для литой алюминиевой обмотки ротора  ,
, 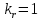 :
: 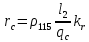 | (22) |
 | (23) |
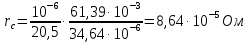

По формуле (21) находим:
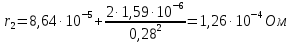
Приведем
 к числу витков обмотки статора по формуле (с учетом для двигателей с
к числу витков обмотки статора по формуле (с учетом для двигателей с 
 :
: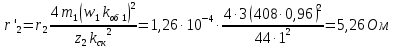
Найдем относительное значение
 :
:
46. Индуктивное сопротивление фазы обмотки статора определяется по формуле (24):
 | (24) |
Где
 - при отсутствии радиальных каналов для обмотки статора;
- при отсутствии радиальных каналов для обмотки статора; – коэффициент магнитной проводимости пазового рассеяния рассчитывается в зависимости от конфигурации паза и расположения в нем проводников обмотки по формуле (25);
– коэффициент магнитной проводимости пазового рассеяния рассчитывается в зависимости от конфигурации паза и расположения в нем проводников обмотки по формуле (25);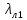 – коэффициент магнитной проводимости лобового рассеяния определяется по формуле (;
– коэффициент магнитной проводимости лобового рассеяния определяется по формуле (; - коэффициент магнитной проводимости дифференциального рассеяния определяется по формуле (29).
- коэффициент магнитной проводимости дифференциального рассеяния определяется по формуле (29).  | (25) |
 | (28) |
 | (29) |
Определение коэффициента магнитной проводимости пазового рассеяния
Коэффициент
 при обмотке с укорочением
при обмотке с укорочением 
определяется по формуле:

Коэффициент
 определяется по формуле:
определяется по формуле: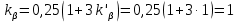


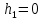 - проводники закреплены пазовой крышкой
- проводники закреплены пазовой крышкойПо формуле (25) находим:
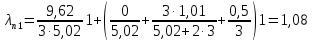
Определение коэффициента магнитной проводимости лобового рассеяния осуществляется по формуле (:

Определение коэффициента магнитной проводимости дифференциального рассеяния
 определяется по формуле (26):
определяется по формуле (26): 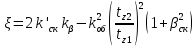 | (26) |
Коэффициент
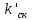 определяется графически в зависимости от соотношения
определяется графически в зависимости от соотношения  .
. 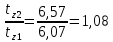
 (по рис. 9.51 д [Копылов] с учетом
(по рис. 9.51 д [Копылов] с учетом 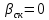 ).
).По формуле (26) находим:

По формуле (29) находим коэффициент магнитной проводимости дифференциального рассеяния:

Определим индуктивное сопротивление фазы обмотки статора по формуле (24):
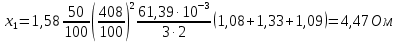
Относительное значение
 :
: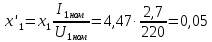
47. Индуктивное сопротивление фазы обмотки ротора определяется по формуле (27):
 | (27) |
Где
 - коэффициент магнитной проводимости пазового рассеяния обмотки ротора, который рассчитывается по формуле (28);
- коэффициент магнитной проводимости пазового рассеяния обмотки ротора, который рассчитывается по формуле (28); 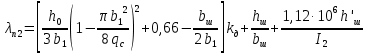 | (28) |
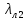 - коэффициент магнитной проводимости лобового рассеяния, который рассчитывается по формуле (29);
- коэффициент магнитной проводимости лобового рассеяния, который рассчитывается по формуле (29);  | (29) |
 - коэффициент магнитной проводимости дифференциального рассеяния, который определяется по формуле (30);
- коэффициент магнитной проводимости дифференциального рассеяния, который определяется по формуле (30); 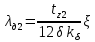 | (30) |
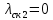 - коэффициент проводимости скоса.
- коэффициент проводимости скоса.
По формуле (28) определяем коэффициент магнитной проводимости пазового рассеяния обмотки ротора, учитывая, что
 :
:
Найдем коэффициент магнитной проводимости лобового рассеяния по формуле (29):
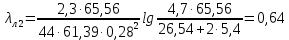
Для определения коэффициента магнитной проводимости дифференциального рассеяния найдем
 по формуле, учитывая, что для закрытых пазов
по формуле, учитывая, что для закрытых пазов  :
:
По формуле (30) находим:
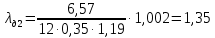
По формуле (27) определим индуктивное сопротивление фазы обмотки ротора:
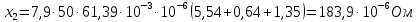
Приводим

к числу витков статора по следующей формуле:
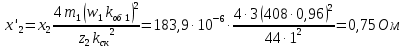
Относительное значение: