ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 19.03.2024
Просмотров: 49
Скачиваний: 0
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
План решения
1. Взять точку M (x ; y ; z) с текущими координатами.
2. Записать координаты направляющего вектора
и координаты точек M1 (x1 ; y1 ; z1) и M2 (x2 ; y2 ; z2), лежащих на прямых.
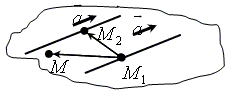
3. Найти координаты векторов
4. Составить уравнение плоскости по формуле
.Решение
M (x ; y ; z), M1 (–2; 1; –3) , M2 (1; –2; 2) ,
Уравнение плоскости
,
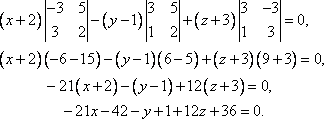,–21x – y + 12z –5 = 0 — уравнение плоскости.
Цит. по: Методическое пособие-тренажер решения задач по высшей математике /
Н.С. Знаенко. — Ульяновск: ИНФОФОНД, 2008. — С. 17–19.
Тема 5. Окружность
Определение 9.9. Геометрическое место точек, расстояние от каждой из которых до данной точки О , называемой центром, есть величина постоянная, называется окружностью.
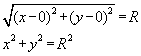— каноническое уравнение окружности.Окружность является частным случаем эллипса, когда большая и малая полуоси равны, с = 0, фокусы сливаются в центр. Эксцентриситет окружности равен нулю.
Цит. по: Математика для экономистов: учебное пособие /
С.И. Макаров. — 2-е изд., стер. — М.: КНОРУС, 2008. — С. 177–178.
2. Нормальное уравнение окружности радиуса R с центром в точках C ( x0 , y0) и O (0, 0) соответственно имеют вид:
(x – x 0
)2 + ( y – y0 )2 = R 2, (4.19)
x 2 + y 2 = R 2. (4.20)
4.47. Составить уравнение окружности, проходящей через точки A (1; 5), B (–4; 0) и D (4; –4).
Решение
Уравнение окружности радиуса R с центром в точке C (x0 , y0) имеет вид (4.19): (x – x0)2 + ( y – y0 )2 = R 2 . Так как точки A, B, D лежат на окружности, то их координаты должны удовлетворять этому уравнению:
Вычитая из первого уравнения системы второе, а затем третье, получим x0 = 1, y0 = 0, а далее и R = 5, т.е. уравнение окружности: ( x – 1)2 + y 2 = 25 (рис. 4.8).
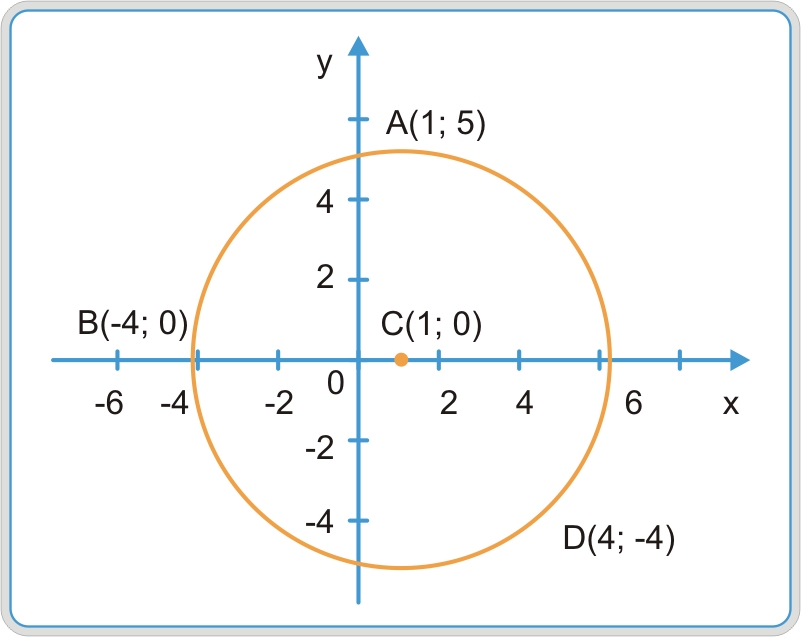
Рис. 4.8
4.48. Найти значение параметра a , при котором окружность x 2 + y 2 – 4x + a = 0 касается прямой
Найти радиус окружности, ее центр и точку касания.Решение
По условию окружность и прямая имеют одну общую точку, следовательно, система
или уравнение
должны иметь единственное решение.
Это произойдет, если дискриминант полученного квадратного уравнения 4 x 2 – 4x + a = 0 будет равен нулю, т.е. D = (–4)2 – 4 × 4 a = 16 (1 – a ) = 0, откуда a = 1.
Решая квадратное уравнение при a = 1, находим x = 0,5, т.е. точка касания
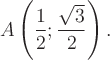
Для определения радиуса окружности приведем ее уравнение к нормальному виду, группируя члены, содержащие x , и дополняя их до полного квадрата:
(x 2 – 4x) + y 2 + 1 = 0, (x2 – 4x + 4) – 4 + y2 + 1 = 0,
откуда ( x – 2)2 + y 2 = 3, т.е. центр окружности (2; 0) и радиус
(рис. 4.9).
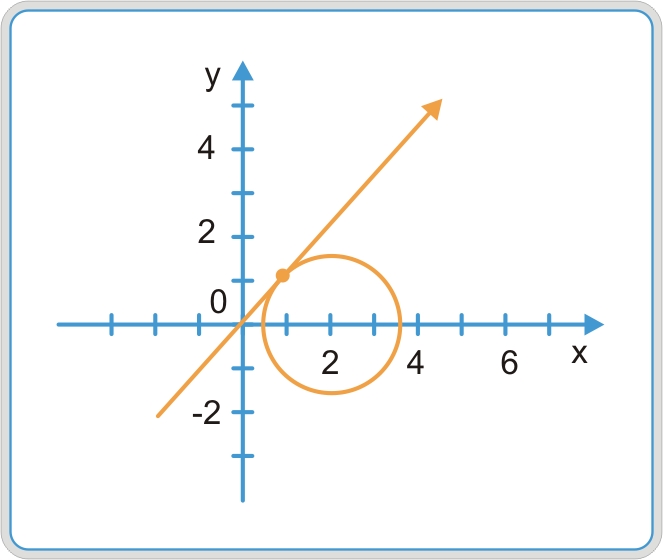
Рис. 4.9
Цит. по: Высшая математика для экономистов:
Практикум для студентов вузов,
обучающихся по экономическим специальностям /
[Н.Ш. Кремер и др]; под ред. проф.Н.Ш. Кремера. —
2-е изд., перераб. и доп. — М.: ЮНИТИ-ДАНА, 2007. —
(Серия «Золотой фонд российских учебников») — С. 110, 112–113.
Определение_9.5.'>Тема 6. Эллипс
Определение 9.5. Геометрическое место точек, сумма расстояний от каждой из которых до двух данных точек, называемых фокусами, есть величина постоянная, называется эллипсом.
— каноническое уравнение эллипса.Исследуем форму эллипса.
1. Найдем точки пересечения с осями.
OX: y = 0, x = ± a ;
OY: x = 0, y = ± b ;
A (a ; 0); B (- a ; 0); C (0; b); D (0; - b).
Определение 9.6.Точки A, B, C, D называются вершинами эллипса.
2. Из вида уравнения следует, что линия симметрична относительно осей OX и OY и начала координат.
3.
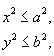
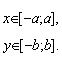
Следовательно, кривая расположена в прямоугольнике со сторонами 2а и 2 b .
Построим данную кривую (рис. 9.9).
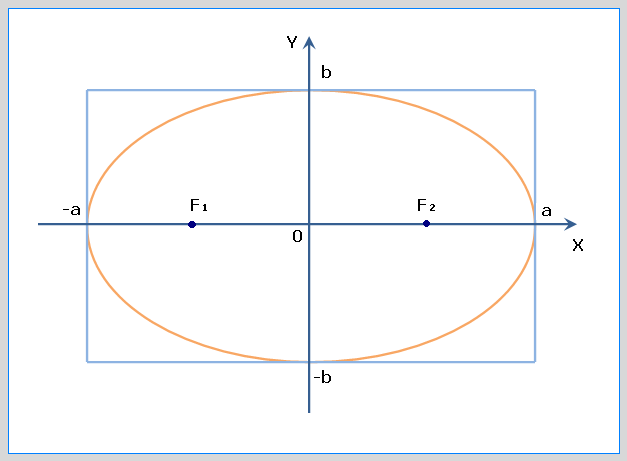
Рис. 9.9
Определение 9.7. Отношение фокусного расстояния к большой оси эллипса называется эксцентриситетом эллипса.
Определение 9.8. Параметр a называется большой полуосью эллипса, параметр b называется малой полуосью эллипса.
Цит. по: Математика для экономистов: учебное пособие /
С.И. Макаров. — 2-е изд., стер. — М.: КНОРУС, 2008. — С. 176–177.
Цит. по: Высшая математика в схемах и таблицах /
Н.С. Знаенко. — Ульяновск: ООО «Вектор-С», 2008. — С. 23.
4.49. Найти полуоси, координаты фокусов и эксцентриситет эллипса 9 x 2 + 4 y 2 = 36.
Решение
Разделив на 36, приведем уравнение к виду
Отсюда следует, что большая полуось эллипса a = 3, а малая полуось b = 2. При этом большая ось эллипса и ее фокусы расположены на оси Oy (рис. 4.10).
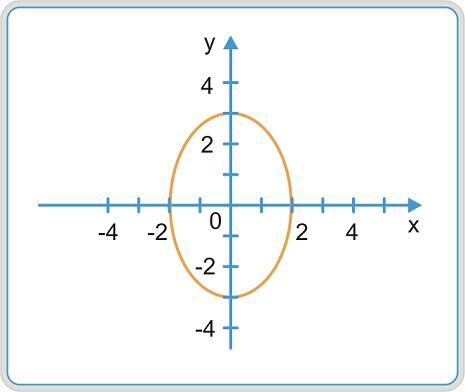
Рис. 4.10
По формуле расстояние от фокуса эллипса до начала координат
т.е. координаты фокусов F1 (0; -√5) и F2 (0; √5). Эксцентриситет эллипса по формуле
Цит. по: Высшая математика для экономистов:
Практикум для студентов вузов,
обучающихся по экономическим специальностям /
[Н.Ш. Кремер и др]; под ред. проф.Н.Ш. Кремера. —
2-е изд., перераб. и доп. — М.: ЮНИТИ-ДАНА, 2007. —
(Серия «Золотой фонд российских учебников») — С. 113.
Тема 7. Гипербола
Определение 9.10. Геометрическое место точек, разность расстояний от каждой из которых до двух данных точек, называемых фокусами, есть величина постоянная, называется гиперболой.
(4.25)— каноническое уравнение гиперболы.
Исследуем форму гиперболы.
1. Найдем точки пересечения с осями.
OX: y = 0,
x = ± 
OY: x = 0,
y ∈ Ø.Определение 9.11. Точки A и B называются вершинами гиперболы.
2. Из вида уравнения следует, что линия симметрична относительно осей OX, OY и начала координат.
3.
Следовательно, кривая расположена вне прямоугольника со сторонами
Построим данную кривую (рис. 9.10).
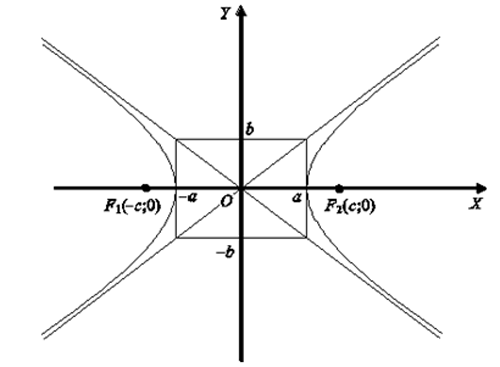
Рис. 9.10
Определение 9.12. Параметр
называется действительной полуосью гиперболы, а параметр b называется мнимой полуосью.Определение 9.13. Прямые
называются асимптотами гиперболы.При возрастании х гипербола неограниченно приближается к асимптотам.
Определение 9.14. Отношение фокусного расстояния гиперболы к ее действительной оси называется эксцентриситетом.
Определение 9.15. Кривые эллипс, гипербола, окружность называются кривыми второго порядка с эксцентриситетом, причем для окружности ε = 0, для эллипса ε ∈ (0; 1) и для гиперболы ε ∈ (1; + ∞). При ε = 1 гипербола вырождается в две параллельные прямые.
Цит. по: Математика для экономистов: учебное пособие /
С.И. Макаров. — 2-е изд., стер. — М.: КНОРУС, 2008. — С. 178–179.
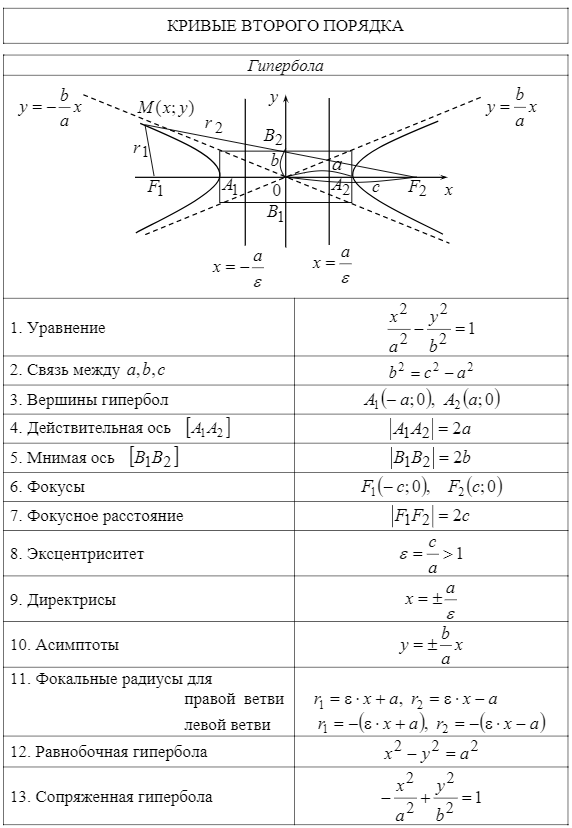
Цит. по: Высшая математика в схемах и таблицах /
Н.С. Знаенко. — Ульяновск: ООО «Вектор-С», 2008. — С. 24.
4.50. Найти координаты центра, вершин и уравнения асимптот гиперболы 9x 2 – 16 y 2 + 144 = 0.
Решение
Приведем уравнение гиперболы к каноническому виду, разделив обе части уравнения на (–144):
Следовательно, гипербола имеет фокусы на оси Oy , ее действительная полуось
а мнимая полуось b = 4 (рис. 9.11).
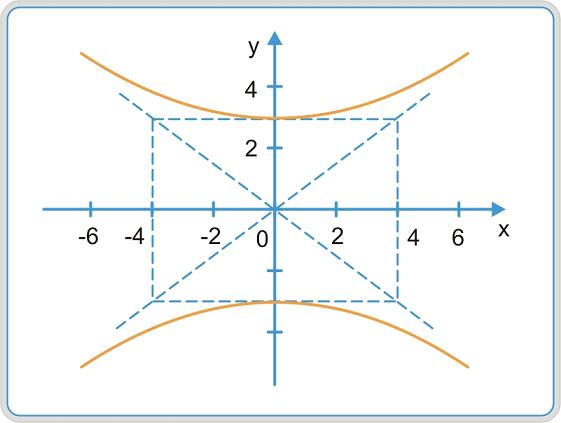
Рис. 9.11
Асимптоты гиперболы по формуле:
или 
Вершины данной гиперболы A1 (0; –3), A
