ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 19.03.2024
Просмотров: 65
Скачиваний: 0
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Тогда
Решение
1. Найдем координаты точки M0. Для этого приравняем в данной системе z к нулю, т.е. пусть z = 0. Тогда система примет вид
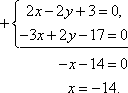
Подставим найденное значение x в первое уравнение системы.
2(–14) – 2y + 3 = 0,
–28 – 2y + 3 = 0,
– 2y – 25 = 0,
Таким образом, M0 (–14; –12,5; 0) .
Замечание
Точка M0 может иметь другие координаты. Всё зависит от того, какое значение и какой переменной придается.
2. Найдем координаты направляющего вектора. Для этого определим координаты нормальных векторов:
и 
Тогда
Таким образом, канонические уравнения имеют вид
Пример 27
Составить канонические уравнения прямой, проходящей через точки с координатами (3; –4; 2) и (2; 5; –1).
План решения
1. Воспользоваться уравнением прямой, проходящей через две точки M1 (x1; y1; z1) и M2 (x2; y2; z2):
Решение
и 
.
Пример 29
Составить канонические уравнения прямой, проходящей через точку M1 (5; –3; 2) и параллельно вектору
План решения
1. Воспользоваться уравнением
где M0 (x0; y0; z0) — координаты точки;
— координаты направляющего вектора.Решение
Пример 31*
Составить уравнение плоскости, которая проходит через ось Oy и точку M1 (3; –2; 5).
План решения
Для составления данного уравнения плоскости следует воспользоваться условием компланарности трех векторов.
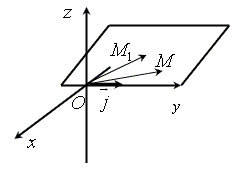
1. Взять точку M (x; y; z) с текущими координатами, лежащую в искомой плоскости.
2. Найти координаты векторов
и 
3. На оси Oy взять единичный вектор
4. Составить уравнение плоскости в виде
т.е. 
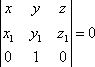.Решение
Возьмем точку M (x; y; z).
Найдем координаты векторов
и 
Составим уравнение
,
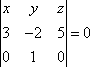,–5x + 3z = 0.
Цит. по: Методическое пособие-тренажер решения задач по высшей математике /
Н.С. Знаенко. — Ульяновск: ИНФОФОНД, 2008. — С. 11–16.
Тема 3. Взаимное расположение прямых
Пример 33*
Вычислить кратчайшее расстояние между прямым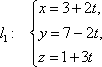и
и 
План решения
1. Найти координаты точек, лежащих на прямых. Если прямая задана параметрическими уравнениями
и 
то M 1 (x 1 ; y 1 ; z 1) и M 2 (x 2 ; y 2 ; z 2).2. Найти координаты направляющих векторов
3. Воспользоваться формулой
,знак «+» берется, если определитель третьего порядка положителен, «–» — в противном случае.
Решение
M1 (3; 7; 1), M 2 (5; 8; 2),
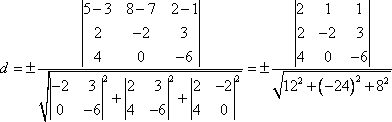;вычислим отдельно
.Таким образом,
Цит. по: Методическое пособие-тренажер решения задач по высшей математике /
Н.С. Знаенко. — Ульяновск: ИНФОФОНД, 2008. — С. 16–17.
Тема 4. Прямая и плоскость
Пример 35*
Найдите координаты точки Q, симметричной точке P (2; 1; –1) относительно плоскости, проходящей через точки M1 (1; 2; –3), M2 (2; 0; 1), M3 (–3; 1; 2).
План решения
1. Составить уравнение плоскости α, проходящей через точки M1 (x1 ; y1 ; z 1), M 2 (x2 ; y2 ; z2), M3 (x3 ; y3 ; z3) по формуле
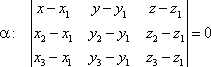
2. Найти точку R, проекцию точки P на плоскость
Для этого:2.1. Составить уравнение перпендикуляра к плоскости
проходящего через точку P , воспользовавшись уравнением 
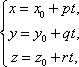где (x 0 ; y 0 ; z 0) — координаты точки P , (p ; q ; r ) — координаты направляющего вектора, в качестве которого выступает нормальный вектор плоскости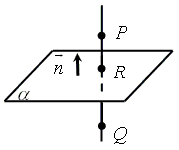 
2.2. Найти точку R, как пересечение прямой PR и плоскости
решив систему уравнений, состоящую из уравнения прямой и плоскости.3. Найти точку Q, которая является вторым концом отрезка PQ, для которого серединой будет точка R — проекция точки P на плоскость
Для этого воспользоваться формулами
x2 = 2x – x1 , y 2 = 2y – y1 , z2 = 2z – z1 , где (x1 ; y1 ; z1) — координаты точки P , (x ;
y ; z) — координаты точки R .
Решение
Составим уравнение плоскости, проходящей через точки M1 , M2 , M3:
,
,
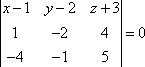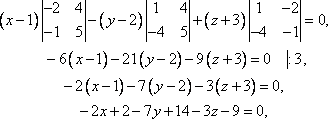
–2x – 7y – 3z + 7 = 0 — уравнение плоскости.Координаты нормального вектора плоскости:
Составим уравнение перпендикуляра к плоскости
проходящего через точку P :
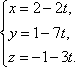
Найдем точку R, пересечения перпендикуляра и плоскости:
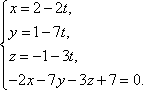
Следовательно,
, 
, 
.Точка
Найдем координаты точки Q по формулам:
,
,
.
Пример 37
Составить уравнение плоскости, проходящей через параллельные прямые
