ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 19.03.2024
Просмотров: 52
Скачиваний: 0
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Даны вершины ΔABC , A (2; –2), B (3; –5), C (5; 7). Напишите уравнения его сторон.
План решения
Каждая сторона треугольника — это прямая, проходящая через две точки.
1. Воспользоваться уравнением прямой, проходящей через две точки M1 (x1 ; y1) и M2 (x2 ; y2):
.2. Определить через какие точки проходит каждая сторона.
Решение
, 
, 
, 
.Приведем уравнение к общему виду
–3(x – 2) = 1(y + 2),
–3x + 6 = y + 2.
–3x – y + 4 = 0 или 3x + y – 4 = 0.
, 
, 
, 
.12(x – 3) = 2(y + 5),
12x – 36 = 2y + 10,
12x – 2y – 46 = 0 или 6x – y – 23 = 0.
, , 
, 
.9(x – 2) = 3(y + 2),
9x – 18 = 3y + 6,
9x – 3y – 24 = 0 или 3x – y – 8 = 0.
В итоге уравнения сторон имеют вид:
AB: 3x + y – 4 = 0, BC: 6x – y – 23 = 0, AC: 3x – y – 8 = 0.
Цит. по: Методическое пособие-тренажер решения задач по высшей математике /
Н.С. Знаенко. — Ульяновск: ИНФОФОНД, 2008. — С. 5–11.
Тема 2. Прямая и плоскость в пространстве
Пример 19*
Найти расстояние от точки P (2; 3; –1) до прямой
План решения
1. Определить координаты направляющего вектора прямой, заданной уравнением
и координаты точки M1 (x0; y0; z0).
2. Найти векторное произведение векторов
и 
3. Найти площадь параллелограмма, построенного на векторах
и 
4. Найти расстояние d, которое является высотой параллелограмма:
, где 
— длина вектора 
Решение
| Решение | Комментарий |
 координаты точки M1 (1; 2; 13), координаты направляющего вектора  Найдем векторное произведение векторов 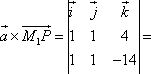и       .Найдем площадь параллелограмма, построенного на векторах и   .Высота параллелограмма и есть искомое расстояние . Тогда  — расстояние от точки P до прямой. | Векторное произведение векторов  и  - это вектор, координаты которого определяются формулой   , т.е. площадь параллелограмма равна длине вектора векторного произведения. |
Пример 21
Найдите координаты точки K пересечения прямой
с плоскостью x + 2y – 3z – 4 = 0.План решения
1. Уравнение прямой записать в параметрическом виде:
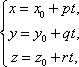
где M0 (x0; y0; z0) — координаты точки,
— координаты направляющего вектора.2. Решить систему уравнений:
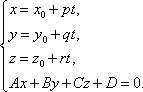
Решение
Из канонического уравнения прямой
возьмем точку M0 (2; 3; –1) и направляющий вектор 
и запишем уравнение прямой в параметрическом виде:
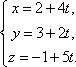
Решим систему уравнений, состоящую из параметрических уравнений и уравнения плоскости:
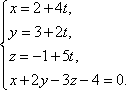
Выражения для x, y и z подставим в последнее уравнение и найдем t :
(2 + 4 t) + 2 (3 + 2t) – 3 (–1 + 5 t) – 4 = 0,
2 + 4 t + 6 + 4 t + 3 – 15 t – 4 = 0,
–7 t + 7 = 0,
t = 1.
Делая обратную подстановку, найдем x, y и z:
, 
, 
.Таким образом, координаты точки пересечения прямой и плоскости K (6; 5; 4).
Пример 23
Найти острый угол между прямыми
План решения
1. Найти координаты направляющих векторов
2. Воспользоваться формулой
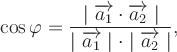
где
— модуль скалярного произведения векторов 
и 
— длины векторов и Решение
Из уравнения прямых имеем
Пример 25
Составить канонические уравнения прямой
План решения
1. Записать канонические уравнения прямой
Чтобы их составить нужно знать координаты точки M0 (x0; y0; z0) и координаты направляющего вектора
2. Найти координаты точки M0. Для этого одну из переменных приравнять к нулю и решить полученную систему.
3. Найти координаты направляющего вектора. В качестве направляющего вектора взять вектор
где
— координаты нормальных векторов плоскостей, определяющих прямую как линию их пересечения, т.е.если
то
