Файл: Цели и задачи дисциплины, ее место и роль в учебном процессе.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 20.03.2024
Просмотров: 83
Скачиваний: 0
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
i,t и rj,t связаны положительной линейной зависимостью, то есть любым изменениям ri,t всегда соответствуют пропорциональные изменения rj,t в тех же направлениях. При = -1 наблюдается абсолютная отрицательная корреляция, когда ri,t и rj,t связаны отрицательной линейной зависимостью. Когда =0, то отсутствует какая-либо взаимосвязь между нормами отдачи двух ценных бумаг.
В общем виде дисперсия портфеля, состоящего из n ценных бумаг, выражается формулой:
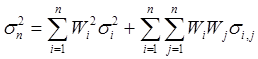
Если вспомнить, что коэффициент корреляции i,j = i,j / ij, то эту формулу можно представить в виде:
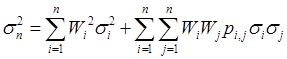
Предположим для примера, что инвестор формирует портфель из трех ценных бумаг акций компаний «А», «В» и «С». При этом из имеющейся у него первоначальной суммы инвестиций он тратит Wa = 0,2 на акции «А», Wb = 0,3 – на акции фирмы «В» и Wc = 0,5 – на акции «С». Чему равен риск и ожидаемая доходность E(rn) такого портфеля? Проведем вычисления, используя ранее полученные величины:
E(rn) = Wa×E(ra)+Wb×E(rb)+Wc×E(rc) = 0,2×0,105+0,3×0,128+0,5×0,194 = 0,156 или 15,6%.
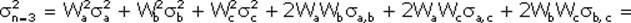
=0,040,014+0,090,019+0,0250,036+20,20,3(-0,012)+20,20,5(-0,006)+20,30,50,006=0,0104
Соотношение риска и доходности портфеля.
Допущение 5.
В своих теоретических исследованиях Марковиц полагал, что значения доходности акций портфеля являются случайными величинами, распределенными по нормальному (Гауссовскому) закону. В этом случае для исчерпывающей характеристики любого портфеля достаточно оценивать лишь два показателя:
ожидаемую доходность и стандартное отклонение как меру риска.
Формула дисперсии портфеля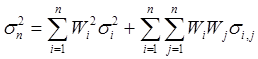 содержит две части: первая часть включает только квадраты величин и всегда положительная. Во вторую часть входят ковариации . Ковариации могут быть отрицательными. Поэтому варьируя состав портфеля за счет изменения:
1) эмитентов акций (при неизменном количестве n акций в портфеле);
2) количества n акций в портфеле;
3) весов акций в портфеле можно воздействовать на риск всего портфеля.
Процесс изменения содержимого портфеля путями а), б), в) с целью снижения риска портфеля называется диверсификацией портфеля. Диверсификация воздействует на риск портфеля и делит его на две части: та часть риска портфеля, которая может быть устранена путем диверсификации, называется диверсифицируемым, или несистематическим риском. Доля же риска, которая не устраняется диверсификацией, носит название недиверсифицируемого, или систематического риска.
Когда в портфель войдут все ценные бумаги, обращающиеся на финансовом рынке, то будет сформирован так называемый рыночный портфель. Риск рыночного портфеля практически полностью является систематическим. Это предельно низкий уровень риска, которого можно достичь за счет диверсификации управляемого портфеля.
Граница эффективных портфелей.
Выберем n акций, зададим два начальных условия:
а) длительность будущего холдингового периода;
б) количество N шагов расчета в прошлом;
После этого вычислим три необходимые характеристики каждой акции:
, и . Зададим после этого произвольную комбинацию весов этих акций (их сумма должна равняться единице) и сформируем некий портфель K. Тогда по выведенным выше формулам можно вычислить ожидаемую доходность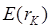 
и стандартное отклонение этого портфеля. Возьмем координатную плоскость и отложим на ней эти значения. В итоге получим точку К на графике с координатами [E(rК); К] (рис. 8).
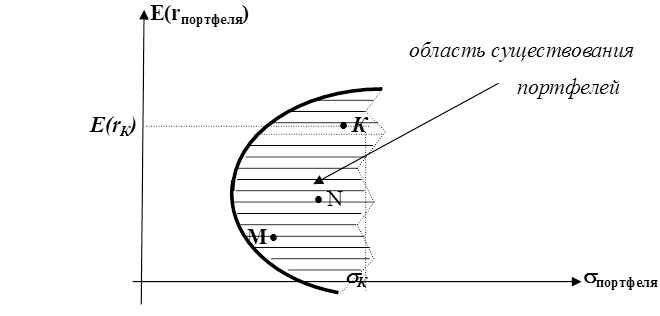
Рис. 8. Граница эффективных портфелей
Изменим веса выбранных n акций, получим уже другой портфель (например, портфель N), для которого также можно вычислить ожидаемую доходность и риск и отложить полученные значения на графике. В результате получим точку
N.
Введем еще одно допущение модели Г. Марковица:
Допущение 6:
каждую акцию портфеля можно разделить на неограниченное число частей, и инвестор в состоянии приобрести любую часть акции. Иными словами, вес каждой акции портфеля может принимать любое значение. Это позволяет из ограниченного числа акций за счет изменения их весов формировать бесконечно много портфелей.
Если для каждого портфеля, созданного из выбранных n акций за счет комбинации их весов, определить ожидаемую доходность и стандартное отклонение, отложить их величины на графике, то получим совокупность точек – область существования портфелей, определяющую все возможные портфели для выбранного количества ценных бумаг. Эта зона имеет характерное «зонтикообразное» очертание. В зависимости от количества и характеристик ценных бумаг, входящих в портфель (ожидаемые доходности, дисперсии, ковариации), эта зона может смещаться влевовправо или вверхвниз, поворачиваться, становиться более пологой или крутой.
Теорема о существовании эффективного множества. Задача инвестора – сформировать из n выбранных акций единственный оптимальный портфель, обеспечивающий этому инвестору максимальную полезность. Ключ к решению проблемы выбора оптимального портфеля лежит в сформулированной Г. Марковицем теореме о существовании эффективного набора портфелей, так называемой границы эффективных портфелей.
Суть теоремы сводится к выводу о том, что любой инвестор должен выбрать из всего бесконечного набора портфелей, сформированных на базе n акций, такой портфель, который удовлетворяет одному из двух (но не двум сразу!) условий:
1) Обеспечивает максимальную ожидаемую доходность при каждом выбранном уровне риска.
2) Обеспечивает минимальный риск для каждой выбранной величины ожидаемой доходности.
Портфели, удовлетворяющие этим условиям, Марковиц относит к эффективным портфелям.
Фактически, суть теоремы Марковица сводится к следующему: если инвестор выбрал n акций, по известным алгоритмам вычислил необходимые характеристики [
; ; ] для каждой акции портфеля, а затем произвольно задал какое-то значение ожидаемой доходности портфеля
= Е*, то найдется только одна комбинация ценных бумаг в портфеле, минимизирующая риск портфеля при заданном значении доходности Е*.
Набор портфелей, которые минимизируют уровень риска при каждой величине ожидаемой доходности, образует так называемое эффективное множество. Если отобразить эффективное множество на координатной плоскости, то получим границу эффективных портфелей (ГЭП) на рисунке ГЭП совпадает с левой границей области существования портфелей.
Общая постановка задачи нахождения границы эффективных портфелей.
Подход Г. Марковица к нахождению оптимального портфеля следующий: пусть имеются n акций, из которых формируется портфель (в нашем примере n = 3). Зададим любое произвольное значение ожидаемой доходности портфеля = Е* , например, Е* = 0,14. Тогда задача инвестора сводится к следующему: из всего бесконечного набора портфелей с ожидаемой доходностью портфеля = 0,14,необходимо найти такой, который обеспечивал бы минимальный уровень риска.
Иными словами, можно задачу инвестора свести к следующему:
необходимо найти минимальное значение дисперсии портфеля
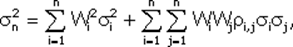
при заданных начальных условиях:
= 
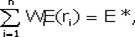
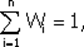
Существует три способа решения подобного рода задач – графический, математический и с использованием компьютерных программ. Далее будет рассмотрен математический метод оптимизации портфеля, наиболее полно отражающий ее сущность.
Математический способ. Для вычисления требуемых величин WА,WВ и WС
используются множители Лагранжа. Рассмотрим последовательность действий в этом методе на примере акций «А», «В» и «С». Подставим вычисленные ранее значения , и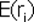
для доходностей этих акций в выражения риска портфеля и доходности портфеля. Тогда задача сводится к следующей - необходимо найти минимальное значение величины:
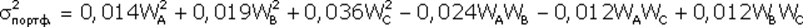
при следующих начальных условиях:
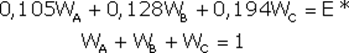
Для решения этой задачи составляется полином Лагранжа L:
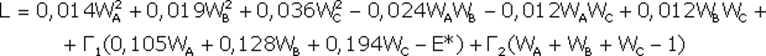
(Г1и Г2 в этом полиноме называются множителями Лагранжа).
После этого вычисляются частные производные полинома по каждой неизвестной величине WА, WВ, WС, Г1, Г2 и приравниваются нулю:
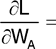0,028WА - 0,024WВ - 0,012WС + 0,105Г1 + Г2 = 0
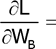- 0,024WА + 0,038WВ + 0,012WС + 0,128Г1 + Г2 = 0
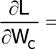-0,012WА + 0,012WВ + 0,072WС + 0,194Г1 + Г2 = 0
0,105WА + 0,128WВ + 0,194WС - E* = 0
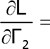WА + WВ + WС -1 = 0
В матричной форме эти уравнения представляются в виде:
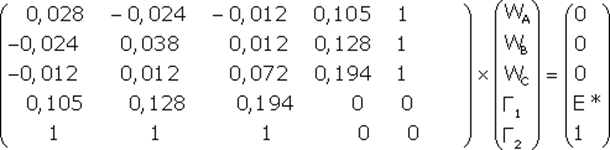
Если обозначить первую матрицу как T, вторую – как W, а третью – как E, то можно это равенство записать в виде матричного уравнения: T×W=E. Чтобы найти значения матрицы W необходимо определить матрицу , являющуюся обратной матрице T. Тогда: W = ×E. Для определения существуют специальные компьютерные программы, хотя это можно сделать и самостоятельно. Вычислив все члены матрицы и умножив матрицу на матрицу E, получим выражения для W
В общем виде дисперсия портфеля, состоящего из n ценных бумаг, выражается формулой:
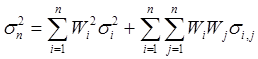
Если вспомнить, что коэффициент корреляции i,j = i,j / ij, то эту формулу можно представить в виде:
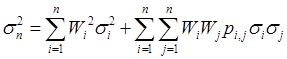
Предположим для примера, что инвестор формирует портфель из трех ценных бумаг акций компаний «А», «В» и «С». При этом из имеющейся у него первоначальной суммы инвестиций он тратит Wa = 0,2 на акции «А», Wb = 0,3 – на акции фирмы «В» и Wc = 0,5 – на акции «С». Чему равен риск и ожидаемая доходность E(rn) такого портфеля? Проведем вычисления, используя ранее полученные величины:
E(rn) = Wa×E(ra)+Wb×E(rb)+Wc×E(rc) = 0,2×0,105+0,3×0,128+0,5×0,194 = 0,156 или 15,6%.
=0,040,014+0,090,019+0,0250,036+20,20,3(-0,012)+20,20,5(-0,006)+20,30,50,006=0,0104
Соотношение риска и доходности портфеля.
Допущение 5.
В своих теоретических исследованиях Марковиц полагал, что значения доходности акций портфеля являются случайными величинами, распределенными по нормальному (Гауссовскому) закону. В этом случае для исчерпывающей характеристики любого портфеля достаточно оценивать лишь два показателя:
ожидаемую доходность и стандартное отклонение как меру риска.Формула дисперсии портфеля
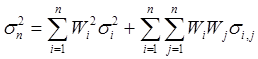содержит две части: первая часть включает только квадраты величин и всегда положительная. Во вторую часть входят ковариации . Ковариации могут быть отрицательными. Поэтому варьируя состав портфеля за счет изменения:
1) эмитентов акций (при неизменном количестве n акций в портфеле);
2) количества n акций в портфеле;
3) весов акций в портфеле можно воздействовать на риск всего портфеля.
Процесс изменения содержимого портфеля путями а), б), в) с целью снижения риска портфеля называется диверсификацией портфеля. Диверсификация воздействует на риск портфеля и делит его на две части: та часть риска портфеля, которая может быть устранена путем диверсификации, называется диверсифицируемым, или несистематическим риском. Доля же риска, которая не устраняется диверсификацией, носит название недиверсифицируемого, или систематического риска.
Когда в портфель войдут все ценные бумаги, обращающиеся на финансовом рынке, то будет сформирован так называемый рыночный портфель. Риск рыночного портфеля практически полностью является систематическим. Это предельно низкий уровень риска, которого можно достичь за счет диверсификации управляемого портфеля.
Граница эффективных портфелей.
Выберем n акций, зададим два начальных условия:
а) длительность будущего холдингового периода;
б) количество N шагов расчета в прошлом;
После этого вычислим три необходимые характеристики каждой акции:
, и . Зададим после этого произвольную комбинацию весов этих акций (их сумма должна равняться единице) и сформируем некий портфель K. Тогда по выведенным выше формулам можно вычислить ожидаемую доходность и стандартное отклонение этого портфеля. Возьмем координатную плоскость и отложим на ней эти значения. В итоге получим точку К на графике с координатами [E(rК); К] (рис. 8). Рис. 8. Граница эффективных портфелей
Изменим веса выбранных n акций, получим уже другой портфель (например, портфель N), для которого также можно вычислить ожидаемую доходность и риск и отложить полученные значения на графике. В результате получим точку
N.
Введем еще одно допущение модели Г. Марковица:
Допущение 6:
каждую акцию портфеля можно разделить на неограниченное число частей, и инвестор в состоянии приобрести любую часть акции. Иными словами, вес каждой акции портфеля может принимать любое значение. Это позволяет из ограниченного числа акций за счет изменения их весов формировать бесконечно много портфелей.
Если для каждого портфеля, созданного из выбранных n акций за счет комбинации их весов, определить ожидаемую доходность и стандартное отклонение, отложить их величины на графике, то получим совокупность точек – область существования портфелей, определяющую все возможные портфели для выбранного количества ценных бумаг. Эта зона имеет характерное «зонтикообразное» очертание. В зависимости от количества и характеристик ценных бумаг, входящих в портфель (ожидаемые доходности, дисперсии, ковариации), эта зона может смещаться влевовправо или вверхвниз, поворачиваться, становиться более пологой или крутой.
Теорема о существовании эффективного множества. Задача инвестора – сформировать из n выбранных акций единственный оптимальный портфель, обеспечивающий этому инвестору максимальную полезность. Ключ к решению проблемы выбора оптимального портфеля лежит в сформулированной Г. Марковицем теореме о существовании эффективного набора портфелей, так называемой границы эффективных портфелей.
Суть теоремы сводится к выводу о том, что любой инвестор должен выбрать из всего бесконечного набора портфелей, сформированных на базе n акций, такой портфель, который удовлетворяет одному из двух (но не двум сразу!) условий:
1) Обеспечивает максимальную ожидаемую доходность при каждом выбранном уровне риска.
2) Обеспечивает минимальный риск для каждой выбранной величины ожидаемой доходности.
Портфели, удовлетворяющие этим условиям, Марковиц относит к эффективным портфелям.
Фактически, суть теоремы Марковица сводится к следующему: если инвестор выбрал n акций, по известным алгоритмам вычислил необходимые характеристики [
; ; ] для каждой акции портфеля, а затем произвольно задал какое-то значение ожидаемой доходности портфеля
= Е*, то найдется только одна комбинация ценных бумаг в портфеле, минимизирующая риск портфеля при заданном значении доходности Е*.Набор портфелей, которые минимизируют уровень риска при каждой величине ожидаемой доходности, образует так называемое эффективное множество. Если отобразить эффективное множество на координатной плоскости, то получим границу эффективных портфелей (ГЭП) на рисунке ГЭП совпадает с левой границей области существования портфелей.
Общая постановка задачи нахождения границы эффективных портфелей.
Подход Г. Марковица к нахождению оптимального портфеля следующий: пусть имеются n акций, из которых формируется портфель (в нашем примере n = 3). Зададим любое произвольное значение ожидаемой доходности портфеля
= Е* , например, Е* = 0,14. Тогда задача инвестора сводится к следующему: из всего бесконечного набора портфелей с ожидаемой доходностью портфеля = 0,14,необходимо найти такой, который обеспечивал бы минимальный уровень риска.Иными словами, можно задачу инвестора свести к следующему:
необходимо найти минимальное значение дисперсии портфеля
при заданных начальных условиях:
= Существует три способа решения подобного рода задач – графический, математический и с использованием компьютерных программ. Далее будет рассмотрен математический метод оптимизации портфеля, наиболее полно отражающий ее сущность.
Математический способ. Для вычисления требуемых величин WА,WВ и WС
используются множители Лагранжа. Рассмотрим последовательность действий в этом методе на примере акций «А», «В» и «С». Подставим вычисленные ранее значения , и
для доходностей этих акций в выражения риска портфеля и доходности портфеля. Тогда задача сводится к следующей - необходимо найти минимальное значение величины: при следующих начальных условиях:
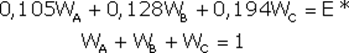
Для решения этой задачи составляется полином Лагранжа L:
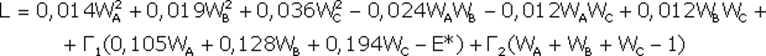
(Г1и Г2 в этом полиноме называются множителями Лагранжа).
После этого вычисляются частные производные полинома по каждой неизвестной величине WА, WВ, WС, Г1, Г2 и приравниваются нулю:
0,028WА - 0,024WВ - 0,012WС + 0,105Г1 + Г2 = 0 - 0,024WА + 0,038WВ + 0,012WС + 0,128Г1 + Г2 = 0 -0,012WА + 0,012WВ + 0,072WС + 0,194Г1 + Г2 = 0 0,105WА + 0,128WВ + 0,194WС - E* = 0 WА + WВ + WС -1 = 0В матричной форме эти уравнения представляются в виде:
Если обозначить первую матрицу как T, вторую – как W, а третью – как E, то можно это равенство записать в виде матричного уравнения: T×W=E. Чтобы найти значения матрицы W необходимо определить матрицу , являющуюся обратной матрице T. Тогда: W = ×E. Для определения существуют специальные компьютерные программы, хотя это можно сделать и самостоятельно. Вычислив все члены матрицы и умножив матрицу на матрицу E, получим выражения для W