ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 27.03.2024
Просмотров: 121
Скачиваний: 0
СОДЕРЖАНИЕ
Вопросы категории 1. Что в разделе «…» обозначается как «…»?
Раздел 1. Основные понятия, гипотезы и принципы.
Раздел 2. Растяжение и сжатие.
Раздел 3. Механические свойства конструкционных материалов.
Раздел 4. Геометрические характеристики плоских сечений.
Раздел 6. Изгиб прямого стержня.
Раздел 7. Перемещения при изгибе.
Раздел 8. Основы теории напряжённого и деформированного состояния в точке тела.
Раздел 9. Сложные виды сопротивления
Раздел 10. Усталостная прочность материалов.
Раздел 11. Устойчивость сжатых стержней.
Раздел 1. Основные понятия, гипотезы и принципы.
Какие виды деформации бруса определяют внутренние силовые факторы ?
Раздел 2. Растяжение и сжатие.
Раздел 3. Механические свойства конструкционных материалов
Раздел 4. Геометрические характеристики плоских сечений.
Раздел 6. Изгиб прямого сечения.
Раздел 7. Перемещения при изгибе.
Раздел 8. Основы теории напряжённого и деформированного состояния в точке.
Раздел 9. Сложные виды сопротивления.
Раздел 10. Усталостная прочность материалов.
Раздел 11. Устойчивость сжатых стержней.
Вопросы категории 3. Выведите зависимости, описывающие…
Раздел 1. Основные понятия, гипотезы и принципы.
Раздел 2. Растяжение и сжатие.
Раздел 3. Механические свойства конструкционных материалов.
Раздел 4. Геометрические характеристики плоских сечений.
Раздел 5. Изгиб прямого стержня.
Раздел 7. Перемещения при изгибе
Раздел 8. Основы теории напряженного и деформированного состояния в точке
Раздел 9. Сложные виды сопротивления
Раздел 10. Усталостная прочность материалов
Раздел 11. Устойчивость сжатых стержней
Дать определение основным видам изгиба.
Какие внутренние силовые факторы возникают в сечении бруса при деформации изгиба ?
Назвать геометрические характеристики плоских сечений и их размерности.
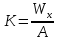 .
.
Размерность этого коэффициента – единицы длины.
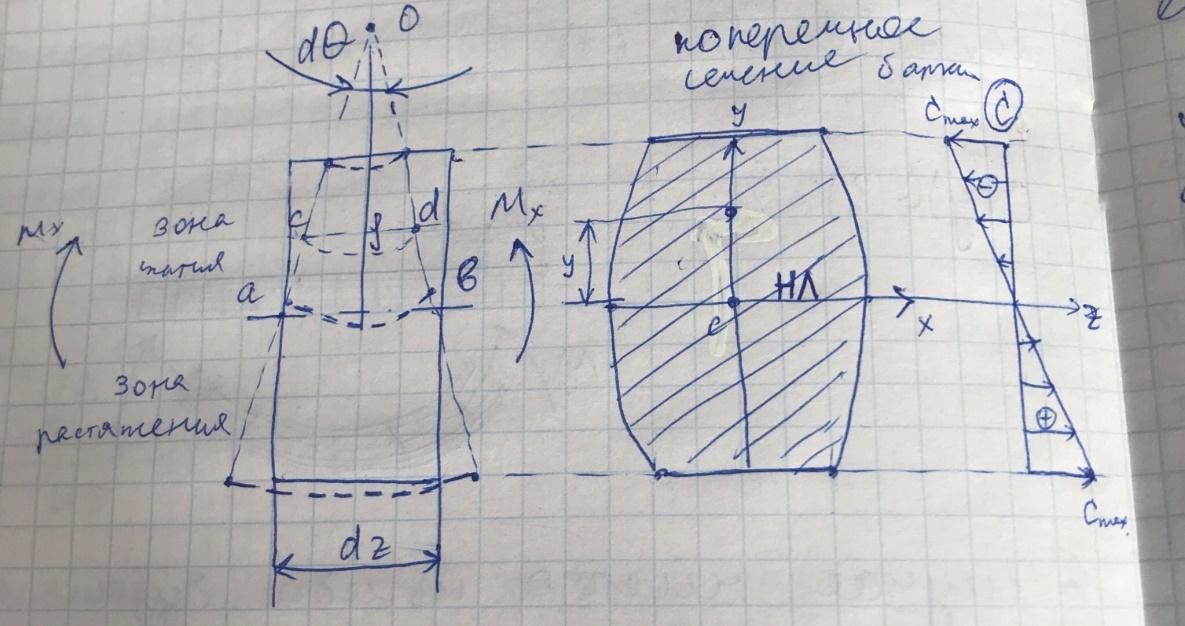
Нейтральный слой – слой, отделяющий зону сжатия от зоны растяжения, т. е. не меняющий своей длины после нагружения.
Нейтральная линия – линия, по которой нейтральный слой пересекается с плоскостью сечения.
Положение
нейтральной линии при прямом изгибе:
нейтральная линия всегда будет проходить
через центр тяжести сечения, также она
будет совпадать с одной из главных осей
сечения, если возникает момент
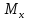 ,
то с осью
,
то с осью
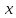 ,
если
,
если
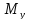 ,
то с осью
,
то с осью
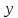 .
.
Раздел 7. Перемещения при изгибе.
Смещение
центра тяжести произвольного сечения
называется прогибом
и является некоторой функцией
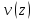 от координаты на длине балки.
от координаты на длине балки.
Пренебрегая
влиянием поперечной силы на искривление
поперечного сечения, можно считать, что
оно поворачивается на угол
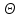 ,
который зависит от положения сечения
на длине балки, то есть угол поворота
тоже будет функцией
,
который зависит от положения сечения
на длине балки, то есть угол поворота
тоже будет функцией
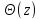 .
.
Угол поворота характерен для любого сечения по длине балки, а прогибы не характеры в тех точках, в которых присутствуют опоры.
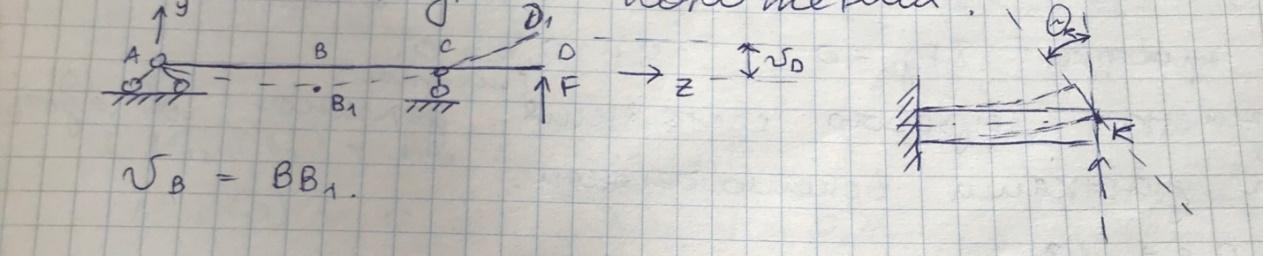
Прогиб
 будем считать положительным, если
перемещение соответствующей точки
происходит вверх, то есть в направлении
положительной оси
будем считать положительным, если
перемещение соответствующей точки
происходит вверх, то есть в направлении
положительной оси
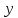 .
Угол поворота
.
Угол поворота
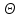 принимается положительным при повороте
сечения против часовой стрелки.
принимается положительным при повороте
сечения против часовой стрелки.
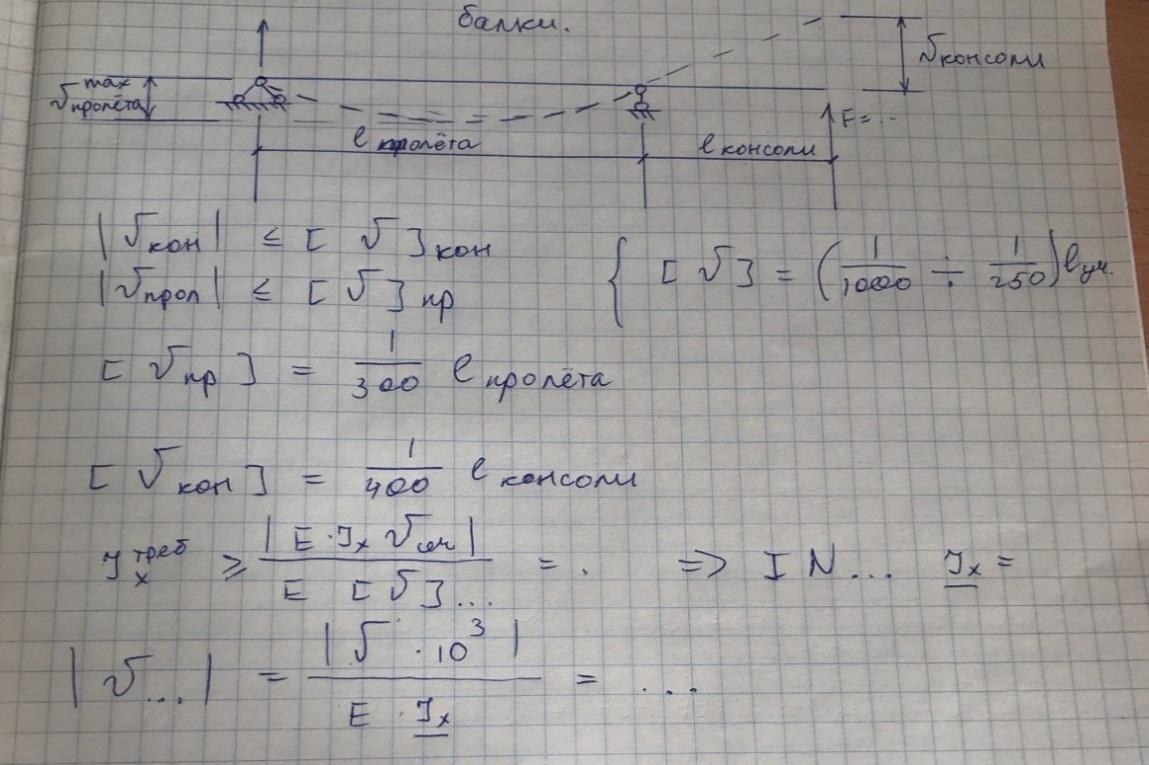
Условие жёсткости при изгибе:
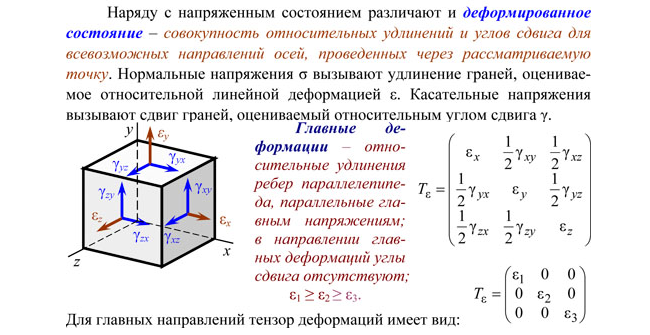
Раздел 8. Основы теории напряжённого и деформированного состояния в точке.
Напряженным состоянием в точке тела называют совокупность нормальных и касательных напряжений, возникающих на всевозможных площадках, проходящих через данную точку.
Изучение напряженного
состояния начинается
с того, что в окрестности исследуемой
точки, например, точки  ,
из нагруженного тела, находящегося в
равновесии, мысленно вырезается
элементарный параллелепипед со
сторонами
,
из нагруженного тела, находящегося в
равновесии, мысленно вырезается
элементарный параллелепипед со
сторонами 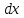 ,
,
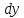 и
и
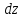 .
.
Ввиду
малости элементарного параллелепипеда
можно считать, что напряжённое состояние
во всех его внутренних точках одинаково
и совпадает с напряжённым
состоянием в
непосредственно исследуемой точке 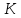 .
.
Элементарный
параллелепипед должен находиться в
равновесии (он не должен вращаться
вокруг оси
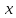 ,
проходящей через точку К), поэтому
суммарный момент всех сил, возникающих
по граням относительно этой оси должен
быть равным нулю:
,
проходящей через точку К), поэтому
суммарный момент всех сил, возникающих
по граням относительно этой оси должен
быть равным нулю:
![]()
В формуле в скобки заключены соответствующие силы, выраженные через касательные и нормальные напряжения, а их плечи указаны за скобками. После элементарных упрощений этого выражения, получим закон парности касательных напряжений:
![]()
Формулировка закона парности касательных напряжений: касательные напряжения на любых двух взаимно перпендикулярных площадках, направленные по перпендикуляру к линии пересечения площадок, равны по величине, притом касательные напряжения либо сходятся к линии пересечения площадок, либо расходятся от неё.
Главными называются площадки, на которых отсутствуют касательные напряжения. Положение главных площадок определяется по формуле
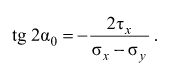
Нормальные напряжения, действующие на главных площадках, называются главными напряжениями.
Они определяются по формуле
![]()
Эквивалентное
напряжение (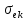 )
– это напряжение, под действием которого
материал в условиях простого
растяжения-сжатия оказывается в равно
опасном состоянии с рассматриваемым
сложным напряженным состоянием.
)
– это напряжение, под действием которого
материал в условиях простого
растяжения-сжатия оказывается в равно
опасном состоянии с рассматриваемым
сложным напряженным состоянием.
Первая теория прочности (теория наибольших нормальных напряжений) связывает разрушение материала с достижением наибольшим нормальным напряжением предельного значения.
Согласно данной теории, напряжённые состояния будут равноопасными, если их наибольшие нормальные напряжения одинаковы.
Так
как при сложном напряженном состоянии
наибольшим нормальным напряжением
является
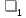 ,
условие прочности будет иметь вид
,
условие прочности будет иметь вид
![]()
Теория иногда применяется при расчёте конструкций из очень хрупких материалов (бетон, камень, кирпич).
Во второй теории прочности (теории наибольших линейных деформаций) в качестве критерия разрушения принято наибольшее относительное удлинение.
Теория утверждает, что напряженные состояния будут равноопасны, если для них равны наибольшие относительные удлинения.
Наибольшее относительное удлинение при трёхосном напряжённом состоянии, согласно обобщённому закону Гука, возникает в направлении первого главного напряжения:

Эта теория прочности так же, как и первая, применима к материалам в хрупком состоянии (высокопрочные инструментальные стали, чугун).
Согласно третьей теории прочности (теории наибольших касательных напряжений), напряжённые состояния будут равноопасными, если их максимальные касательные напряжения равны.
Ввиду того, что при сложном напряженном состоянии элемента
![]()
а при одноосном растяжении образца
![]()
условие прочности приобретает вид:
![]()
Третья теория даёт хорошие результаты для пластичных материалов с одинаковым пределом текучести при растяжении и сжатии.
Согласно четвёртой теории прочности (энергетической теории), напряжённые состояния равноопасны, если для них равны удельные потенциальные энергии изменения формы.
При сложном напряжённом состоянии удельная потенциальная энергия изменения формы определяется по выражению
![]()

Теория прочности Мора (пятая гипотеза прочности).
Теория прочности Мора позволяет учесть различное сопротивление материалов растяжению и сжатию. Например, бетон, который имеет высокую прочность на сжатие, но совершенно не может работать на растяжение.


