ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 27.03.2024
Просмотров: 91
Скачиваний: 0
СОДЕРЖАНИЕ
Вопросы категории 1. Что в разделе «…» обозначается как «…»?
Раздел 1. Основные понятия, гипотезы и принципы.
Раздел 2. Растяжение и сжатие.
Раздел 3. Механические свойства конструкционных материалов.
Раздел 4. Геометрические характеристики плоских сечений.
Раздел 6. Изгиб прямого стержня.
Раздел 7. Перемещения при изгибе.
Раздел 8. Основы теории напряжённого и деформированного состояния в точке тела.
Раздел 9. Сложные виды сопротивления
Раздел 10. Усталостная прочность материалов.
Раздел 11. Устойчивость сжатых стержней.
Раздел 1. Основные понятия, гипотезы и принципы.
Какие виды деформации бруса определяют внутренние силовые факторы ?
Раздел 2. Растяжение и сжатие.
Раздел 3. Механические свойства конструкционных материалов
Раздел 4. Геометрические характеристики плоских сечений.
Раздел 6. Изгиб прямого сечения.
Раздел 7. Перемещения при изгибе.
Раздел 8. Основы теории напряжённого и деформированного состояния в точке.
Раздел 9. Сложные виды сопротивления.
Раздел 10. Усталостная прочность материалов.
Раздел 11. Устойчивость сжатых стержней.
Вопросы категории 3. Выведите зависимости, описывающие…
Раздел 1. Основные понятия, гипотезы и принципы.
Раздел 2. Растяжение и сжатие.
Раздел 3. Механические свойства конструкционных материалов.
Раздел 4. Геометрические характеристики плоских сечений.
Раздел 5. Изгиб прямого стержня.
Раздел 7. Перемещения при изгибе
Раздел 8. Основы теории напряженного и деформированного состояния в точке
Раздел 9. Сложные виды сопротивления
Раздел 10. Усталостная прочность материалов
Раздел 11. Устойчивость сжатых стержней
Дать определение основным видам изгиба.
Какие внутренние силовые факторы возникают в сечении бруса при деформации изгиба ?
Назвать геометрические характеристики плоских сечений и их размерности.
На подвижной траверсе установлен датчик силы, к которому через переходник крепится захват. Исследуемый образец закрепляется в захватах. Устанавливается нулевое значение текущего усилия. Поступательное движение траверсы вызывает деформацию образца.
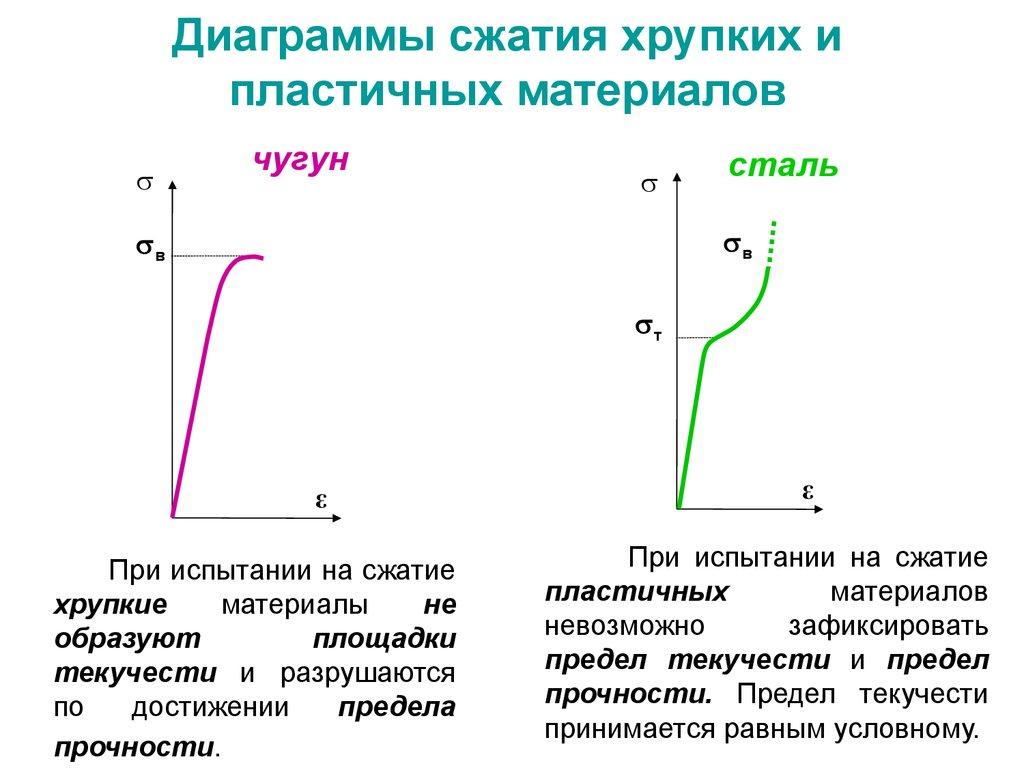
Испытанию на сжатие подвергают хрупкие материалы, которые, как правило, лучше сопротивляются сжатию, чем растяжению. Для их расчёта на прочность необходимо знать характеристики материалов, получаемые при испытании на сжатие.
Диаграмма растяжения малоуглеродистой стали:
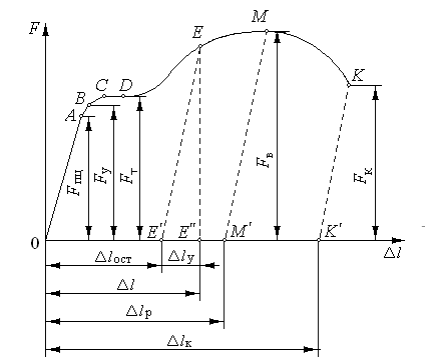
OA – прямая, участок упругой деформации материала. На всём участке справедлив закон Гука;
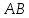 – закон
Гука нарушается, но при снятии нагрузки
образец полностью восстанавливает свои
первоначальные размеры;
– закон
Гука нарушается, но при снятии нагрузки
образец полностью восстанавливает свои
первоначальные размеры;
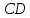 – площадка
текучести, удлинение образца происходит
при постоянной нагрузке.
– площадка
текучести, удлинение образца происходит
при постоянной нагрузке.
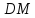 – зона
упрочнения, требуется увеличение
нагрузки для дальнейшего растяжения
образца;
– зона
упрочнения, требуется увеличение
нагрузки для дальнейшего растяжения
образца;
 – точка,
соответствующая наибольшей силе,
достигнутой при испытании;
– точка,
соответствующая наибольшей силе,
достигнутой при испытании;
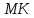 – зона
местных деформаций, на образце появляется
сужение, в которой и происходит основной
рост деформаций;
– зона
местных деформаций, на образце появляется
сужение, в которой и происходит основной
рост деформаций;
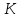 – точка
диаграммы, соответствующая моменту
разрыва образца.
– точка
диаграммы, соответствующая моменту
разрыва образца.
Диаграммы сжатия пластичных и хрупких материалов:
Основные прочностные характеристики:
1. Предел пропорциональности – максимальное напряжение, при котором ещё соблюдается прямая пропорциональность между напряжениями и деформациями,
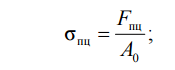
2. Предел текучести – наименьшее напряжение, при котором образец деформируется без заметного увеличения нагрузки,
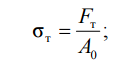
3. Временное сопротивление (предел прочности) – напряжение, соответствующее наибольшей нагрузке, достигнутой при испытании образца,
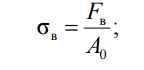
4. Истинное сопротивление разрыву – напряжение, соответствующее моменту разрыва образца,
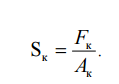
Основные характеристики пластичности:
1. Относительное равномерное остаточное удлинение – необратимая часть деформации, соответствующая временному сопротивлению,
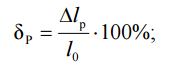
где
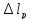 – соответствующее ему абсолютное
удлинение;
– соответствующее ему абсолютное
удлинение;
2. Относительное удлинение после разрыва:
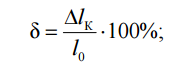
3. Относительное сужение после разрыва:
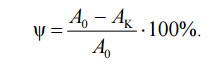
Основные факторы, влияющие на механические свойства материалов:
1. Температура.
2. Радиационное облучение.
3. Прокатка.
4. Наклёп.
5. Поверхностная обработка.
6. Термообработка.
7. Фактор времени.
8. Легирующие добавки.
Раздел 4. Геометрические характеристики плоских сечений.
При определении положения центра тяжести сечения необходимо определять значения статических моментов этого сечения.
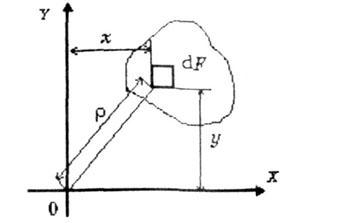
Статическими
моментами площади сечения
относительно осей
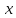 и
и
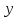 называются определенные интегралы
вида:
называются определенные интегралы
вида:
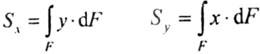
где
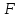 – площадь сечения;
– площадь сечения;
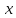 и
и
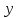 - координаты элемента площади
- координаты элемента площади
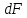 .
.
Если известно положение центра тяжести сечения, то статические моменты сечения могут быть подсчитаны по простым формулам, а именно
![]()
где
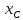 и
и
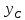 – координаты центра тяжести сечения.
– координаты центра тяжести сечения.
Статический момент сечения относительно оси, проходящей через центр тяжести, равен нулю.


Координатные оси, для которых центробежный момент инерции равен нулю, называются главными осями, а моменты инерции относительно этих осей – главными моментами инерции.

Осевой момент сопротивления – отношение момента инерции относительно оси к расстоянию от неё до наиболее удалённой точки сечения:
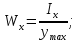
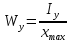 .
.
Полярный момент сопротивления сечения – это отношение полярного момента инерции к расстоянию от полюса до наиболее удалённой точки сечения:
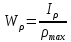 .
.
Раздел 5. Сдвиг. Кручение.
Чистый сдвиг (или срез) – это такой вид нагружения, при котором в сечении стержня появляется поперечная сила, а остальные ВСФ равны нулю.

Большинство соединений в машиностроении (резьбовые, сварочные, заклёпочные, шпоночные и т. д.) работают на срез.
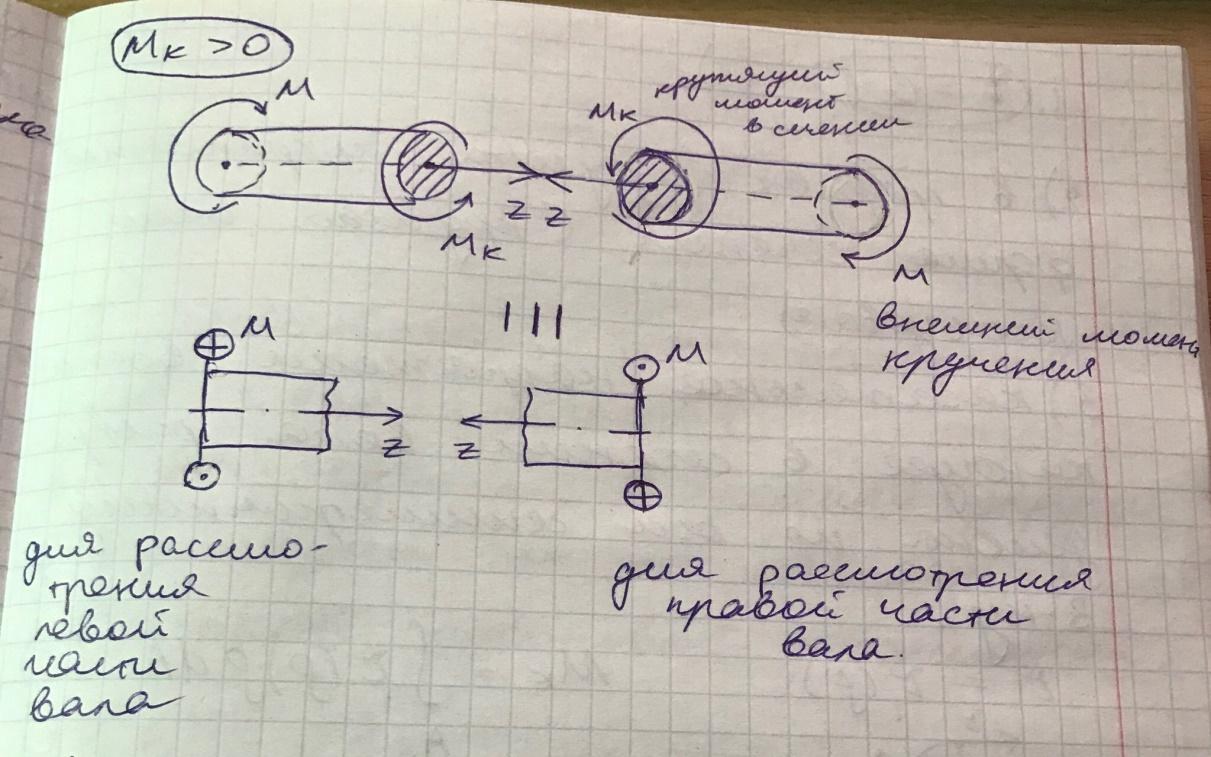
Кручение
– это такой вид нагружения при котором
в сечении стержня возникает только
крутящий момент
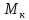 ,
а остальные ВСФ равны нулю.
,
а остальные ВСФ равны нулю.
Брус, работающий на кручение, называют валом.
Деформация
кручения возникнет в том случае, если
на вал воздействуют внешние скручивающие
моменты, то есть моменты относительно
оси
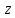 .
.
Раздел 6. Изгиб прямого сечения.
Виды изгиба:
1. Прямой изгиб – изгиб, при котором вся внешняя нагрузка находится в одной плоскости, и сам стержень изгибается в этой же плоскости.
При
чистом
изгибе
в сечении стержня возникает изгибающий
момент
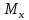 или
или
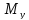 ,
а остальные ВСФ равны нулю.
,
а остальные ВСФ равны нулю.
При
поперечном
изгибе
в сечении стержня одновременно возникают
поперечная сила и изгибающий момент ( и
и
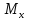 или
или
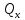 и
и
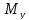 – 2 ВСФ).
– 2 ВСФ).
2. Косой изгиб.
При плоском косом изгибе внешняя нагрузка, приложенная к стержню, лежит в одной плоскости, но не совпадает ни с одной из главных плоскостей стержня.
В
этом случае сам стержень будет изгибаться
в плоскости, не совпадающей с плоскостью
воздействия нагрузки, т. е. косо по
отношению к ней (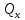 ,
,
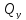 ,
,
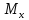 и
и
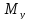 – 4 ВСФ).
– 4 ВСФ).
При
пространственном
изгибе
внешняя нагрузка, приложенная к стержню,
лежит одновременно в двух или более
плоскостях (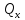 ,
,
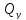 ,
,
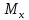 и
и
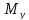 – 4 ВСФ).
– 4 ВСФ).
Внешняя нагрузка обычно задана, поэтому для нахождения всех действующих на балку сил необходимо вычислить реакции опор. Наименьшее число связей, обеспечивающее неподвижность балки в одной плоскости, равно трём. Уравнения равновесия, из которых определяются опорные реакции, могут быть записаны тремя различными способами:
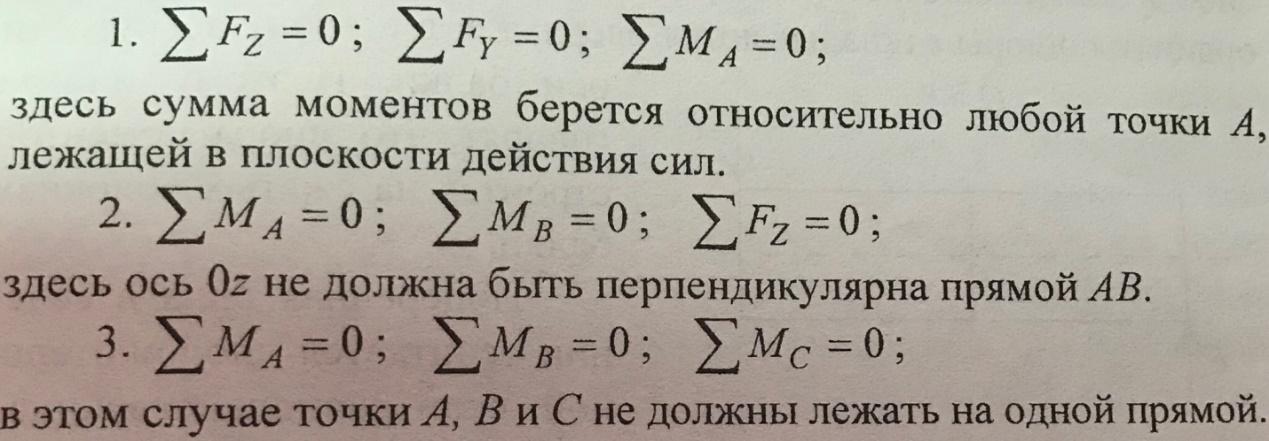
При расчётах балок на прочность необходимо знать, как ВСФ меняются по длине балки и уметь строить их эпюры.
Эта задача решается на основе метода сечений, согласно которому поперечная сила в произвольном сечении балки находится как алгебраическая сумма внешних сил, действующих на отсечённую часть балки.
Аналогично определяется и изгибающий момент в сечении, который вычисляется как алгебраическая сумма моментов относительно центра тяжести данного сечения всех внешних сил, приложенных к отсечённой части балки.
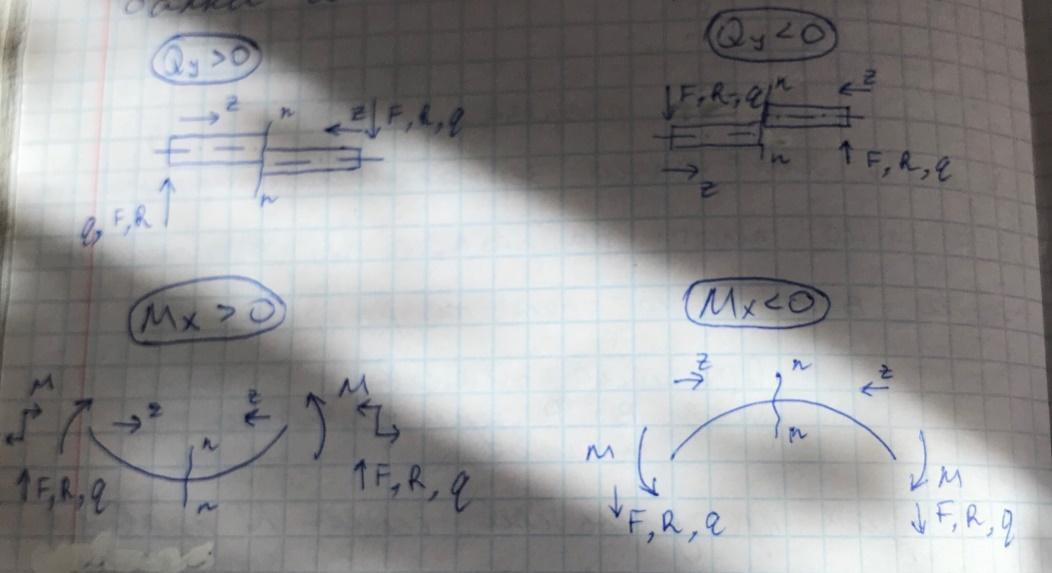
Правило знаков для ВСФ при изгибе:
1.
Для продольной силы
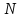 :
:
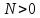 ,
если стержень работает на растяжение;
,
если стержень работает на растяжение;
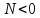 ,
если стержень работает на сжатие.
,
если стержень работает на сжатие.
2.
Поперечная сила
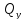 будет считаться положительной, если
она стремится повернуть рассматриваемую
часть балки по ходу часовой стрелки.
будет считаться положительной, если
она стремится повернуть рассматриваемую
часть балки по ходу часовой стрелки.
3.
Изгибающий момент
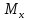 будет
считаться положительным, если он будет
стремится отогнуть рассматриваемую
часть стержня вверх (стремится вызвать
растяжение нижних продольных волокон
балки и сжатие верхних продольных
волокон балки).
будет
считаться положительным, если он будет
стремится отогнуть рассматриваемую
часть стержня вверх (стремится вызвать
растяжение нижних продольных волокон
балки и сжатие верхних продольных
волокон балки).
Наиболее
рациональное сечение выбирается исходя
из момента сопротивления сечения балки
при изгибе, а также площади поперечного
сечения балки. Коэффициент
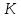 определяется как отношение момента
сопротивления сечения балки к площади
этого сечения:
определяется как отношение момента
сопротивления сечения балки к площади
этого сечения:

