ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 27.03.2024
Просмотров: 96
Скачиваний: 0
СОДЕРЖАНИЕ
Вопросы категории 1. Что в разделе «…» обозначается как «…»?
Раздел 1. Основные понятия, гипотезы и принципы.
Раздел 2. Растяжение и сжатие.
Раздел 3. Механические свойства конструкционных материалов.
Раздел 4. Геометрические характеристики плоских сечений.
Раздел 6. Изгиб прямого стержня.
Раздел 7. Перемещения при изгибе.
Раздел 8. Основы теории напряжённого и деформированного состояния в точке тела.
Раздел 9. Сложные виды сопротивления
Раздел 10. Усталостная прочность материалов.
Раздел 11. Устойчивость сжатых стержней.
Раздел 1. Основные понятия, гипотезы и принципы.
Какие виды деформации бруса определяют внутренние силовые факторы ?
Раздел 2. Растяжение и сжатие.
Раздел 3. Механические свойства конструкционных материалов
Раздел 4. Геометрические характеристики плоских сечений.
Раздел 6. Изгиб прямого сечения.
Раздел 7. Перемещения при изгибе.
Раздел 8. Основы теории напряжённого и деформированного состояния в точке.
Раздел 9. Сложные виды сопротивления.
Раздел 10. Усталостная прочность материалов.
Раздел 11. Устойчивость сжатых стержней.
Вопросы категории 3. Выведите зависимости, описывающие…
Раздел 1. Основные понятия, гипотезы и принципы.
Раздел 2. Растяжение и сжатие.
Раздел 3. Механические свойства конструкционных материалов.
Раздел 4. Геометрические характеристики плоских сечений.
Раздел 5. Изгиб прямого стержня.
Раздел 7. Перемещения при изгибе
Раздел 8. Основы теории напряженного и деформированного состояния в точке
Раздел 9. Сложные виды сопротивления
Раздел 10. Усталостная прочность материалов
Раздел 11. Устойчивость сжатых стержней
Дать определение основным видам изгиба.
Какие внутренние силовые факторы возникают в сечении бруса при деформации изгиба ?
Назвать геометрические характеристики плоских сечений и их размерности.
![]()
Линейная деформация (деформация растяжения) – деформация, при которой происходит изменение только одного линейного размера тела.
Количественно
она характеризуется абсолютным
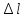 и относительным
и относительным
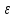 удлинением.
удлинением.
![]()
где
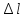 – абсолютное удлинение;
– абсолютное удлинение;
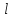 и
и
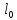 –
конечная и начальная длина тела.
–
конечная и начальная длина тела.
![]()
![]()
где
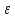 – относительное удлинение тела;
– относительное удлинение тела;
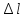 – абсолютное удлинение тела;
– абсолютное удлинение тела;
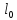 –начальная
длина тела.
–начальная
длина тела.
При
продольном осевом нагружении
(растяжении-сжатии)
в поперечных сечениях бруса имеют
место только нормальные
напряжения 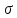 .
.
Поэтому для обеспечения прочности стержней и стержневых систем достаточно выполнение условия:
![]()

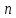 –
коэффициент
запаса прочности, устанавливаемый
нормативными документами.
–
коэффициент
запаса прочности, устанавливаемый
нормативными документами.
Раздел 3. Механические свойства конструкционных материалов.
Критерием оценки прочности элементов является условие, при котором напряжения, возникающие под действием внешних нагрузок не должны превышать допустимых значений.
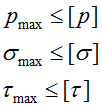
В механике основными видами расчетов на прочность являются:
-
проектировочный расчет (подбор размеров сечений);
-
проверка на прочность;
-
определение грузоподъёмности.
Прочностные расчеты выполняются в несколько этапов:
1. При необходимости определяются опорные реакции.
2. Рассчитываются внутренние силовые факторы и строятся их эпюры.
3. Определяются наиболее нагруженные участки либо сечения бруса.
4. В зависимости от условия задачи выполняется необходимый расчёт.
Раздел 4. Геометрические характеристики плоских сечений.
Моменты инерции сечений простой формы:
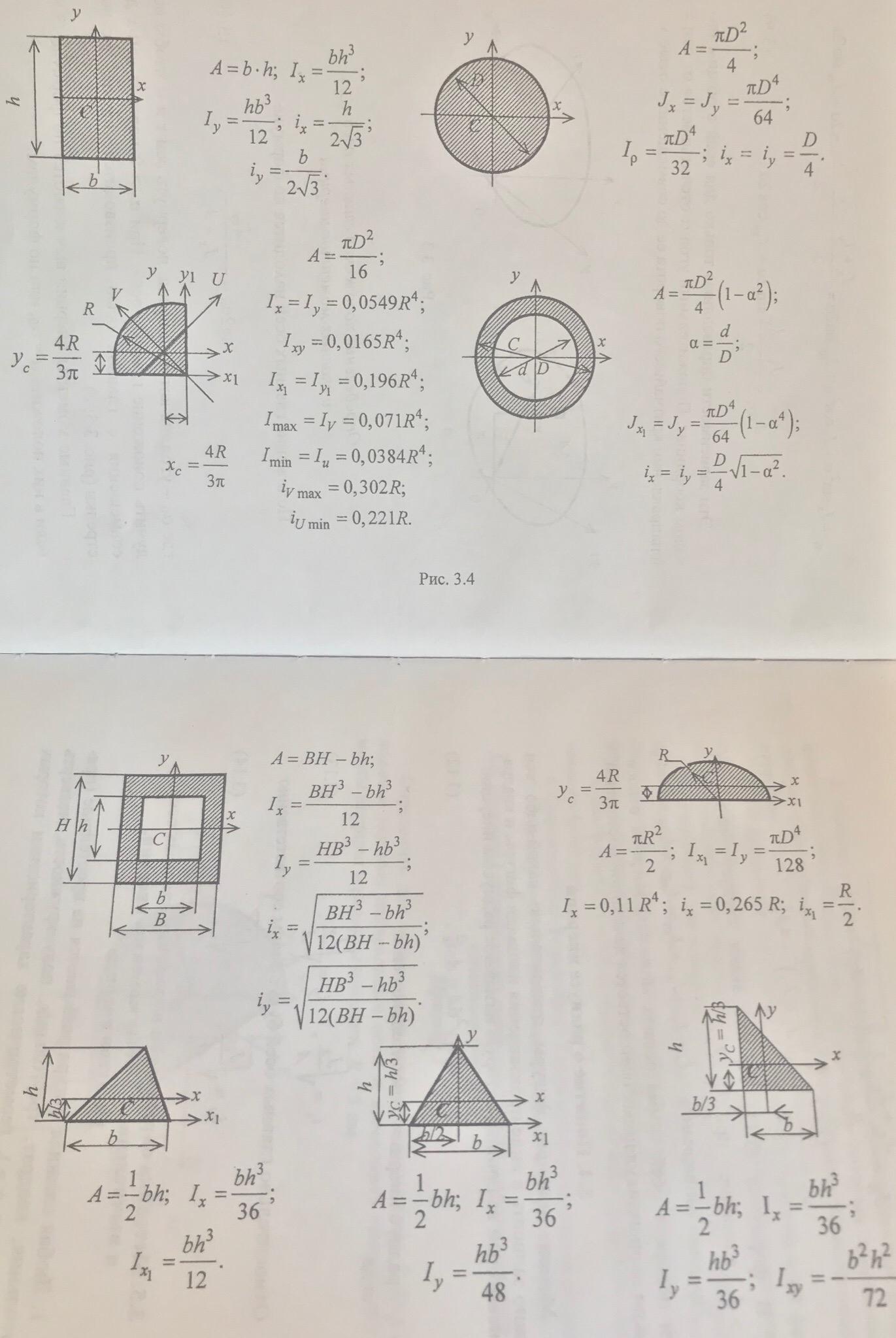
Если
оси
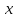 ,
,
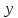 параллельны центральным осям
параллельны центральным осям
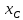 ,
,
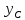 ,
то справедливы следующие отношения:
,
то справедливы следующие отношения:
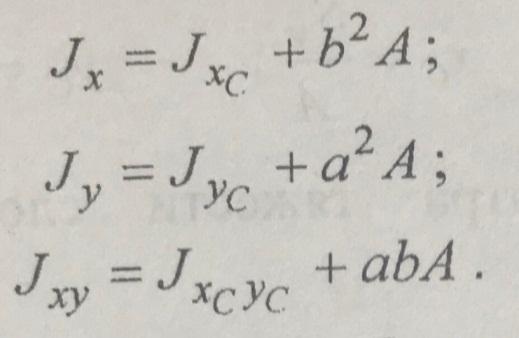
Здесь
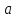 и
и
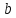 – координаты точки O
(с учетом знаков), то есть нового начала
координат в старой системе координат
– координаты точки O
(с учетом знаков), то есть нового начала
координат в старой системе координат
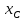 ,
,
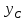 .
.
Первые слагаемые в правых частях равенств являются собственными моментами инерции фигуры, а вторые слагаемые переносными моментами инерции.
При
повороте осей (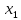 ,
,
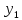 )
на какой-либо угол
)
на какой-либо угол
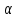 по отношению к исходным осям моменты
инерции изменяются:
по отношению к исходным осям моменты
инерции изменяются:
![]()
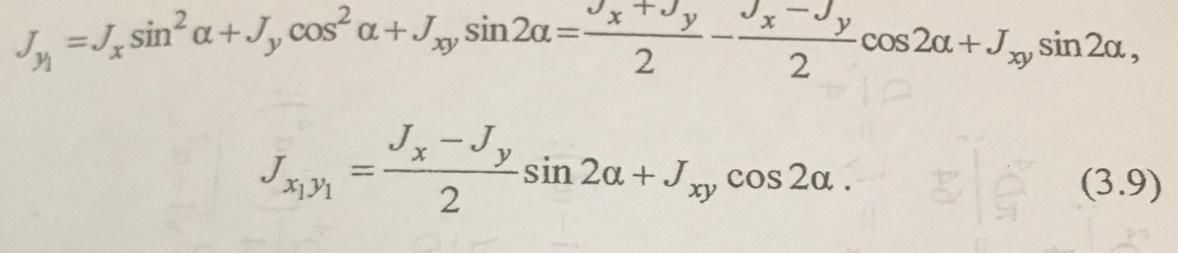
Эти
зависимости справедливы только для
осей с общим началом координат.
Положительный угол
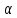 отсчитывается от оси
отсчитывается от оси
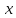 в направлении кратчайшего поворота её
до совмещения с осью
в направлении кратчайшего поворота её
до совмещения с осью
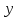 .
.
Положение главных осей находится по формуле:
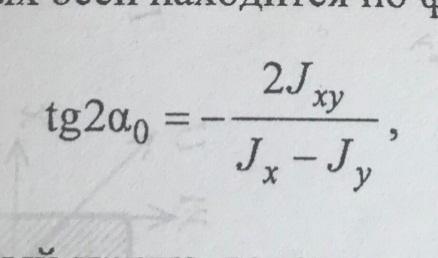
где
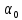 – угол, на который нужно повернуть оси
– угол, на который нужно повернуть оси
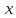 и
и
 ,
чтобы получить положение главных осей.
При
,
чтобы получить положение главных осей.
При
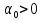 поворот оси
поворот оси
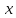 до совмещения с главной осью производится
против часовой стрелки
до совмещения с главной осью производится
против часовой стрелки
Методика определения положения главных осей и вычисления главных моментов инерции, радиусов инерции:
1. Любая сложная фигура разбивается на простейшие (прямоугольник, квадрат, треугольник, полуокружность, четверть окружности и так далее), геометрические характеристики которых известны.
2. Проводится произвольная система прямоугольных координат (вспомогательные оси), относительно которых положение центров тяжести любой простейшей фигуры является величиной известной.
3.
По формулам определяется центр тяжести
всей фигуры и проводятся центральные
оси
 ,
,
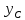 ,
которые
параллельны центральным осям простейших
фигур.
,
которые
параллельны центральным осям простейших
фигур.
4. Используя зависимость изменения моментов инерции при параллельном переносе осей, определяют моменты инерции и центробежный момент инерции всей фигуры относительно центральных осей.
5.
По формуле вычисляют положение главных
осей инерции (угол
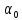 ).
).
6. Определяют по формулам главные моменты инерции.
7. По формулам вычисляют главные радиусы инерции.
Раздел 5. Сдвиг. Кручение.

Большинство соединений в машиностроении (резьбовые, сварные, заклёпочные, шпоночные и т. д.) работают на срез.

Выделим
в окрестности точки
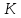 ,
находящейся в плоскости среза, бесконечно
малую площадку и рассмотрим её отдельно.
,
находящейся в плоскости среза, бесконечно
малую площадку и рассмотрим её отдельно.
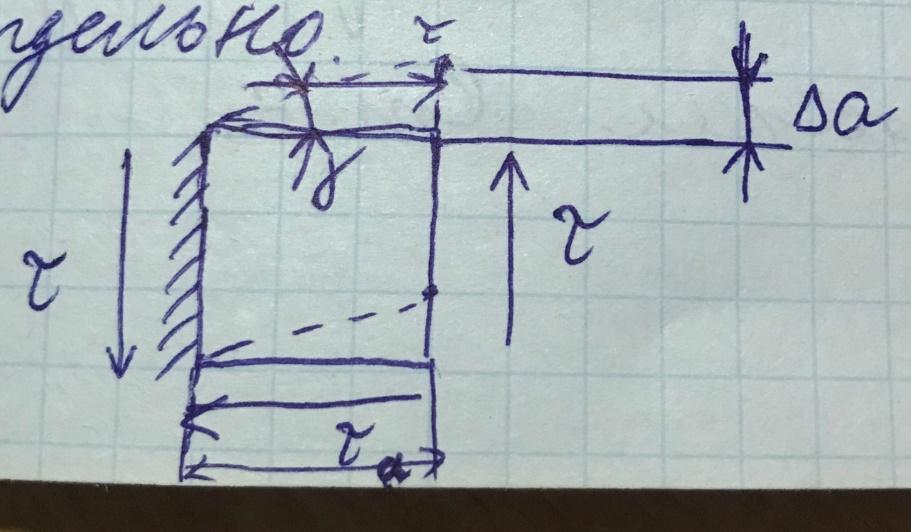
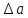 – величина
абсолютного сдвига или абсолютное
смещение грани;
– величина
абсолютного сдвига или абсолютное
смещение грани;
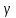 – угол
сдвига;
– угол
сдвига;
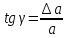 .
.
В
пределах упругих деформаций величины
углов
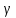 будут незначительными, для них справедливо,
что
будут незначительными, для них справедливо,
что
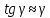 (в
радианах).
(в
радианах).
Тогда
 ,
в таком виде величину
,
в таком виде величину
 можно
рассматривать как относительную
сдвиговую деформацию.
можно
рассматривать как относительную
сдвиговую деформацию.
По диаграмме растяжения может быть построена диаграмма чистого сдвига материала.
Диаграмму смотри в разделе 3 (первый вопрос)
В
точке
 происходит срез образца.
происходит срез образца.
Точке
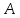 по оси
по оси
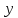 соответствует
соответствует
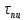 – предел пропорциональности по
касательному напряжению.
– предел пропорциональности по
касательному напряжению.
Закон Гука в чистом виде:
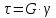 ,
,
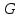 – модуль
сдвига, модуль упругости 2 рода (
– модуль
сдвига, модуль упругости 2 рода (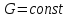 ,
для упругих материалов).
,
для упругих материалов).
Для изотропных материалов (металлов):
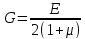 ,
,
где
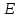 – модуль Юнга,
– модуль Юнга,
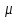 – коэффициент Пуассона.
– коэффициент Пуассона.
Следовательно,
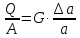 ,
,
следовательно
 .
.
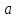 – это
характерный габаритный размер плоскости,
через которую проходит разрез.
– это
характерный габаритный размер плоскости,
через которую проходит разрез.
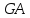 – жёсткость
сечения при сдвиге.
– жёсткость
сечения при сдвиге.
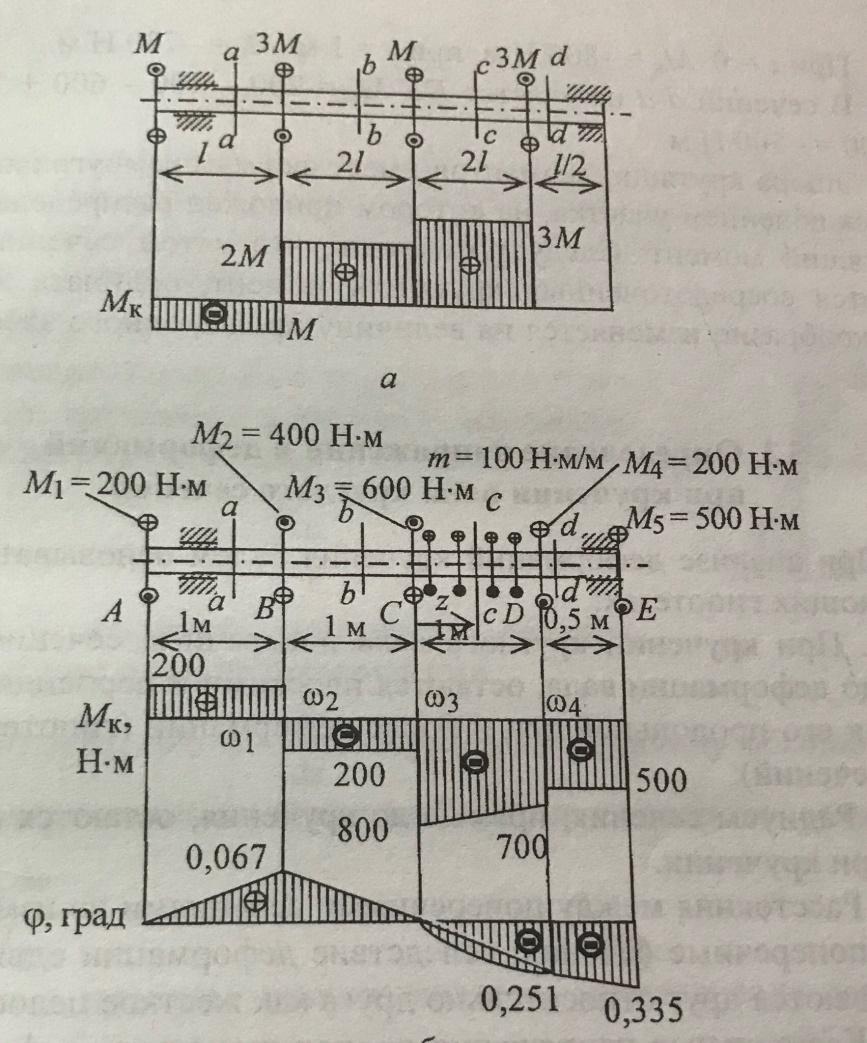
Построение эпюры крутящих моментов.
На участке АВ из условия равновесия левой части от сечения а-а получаем Мк=200 Нм;
В сечении b-b на участке ВС получаем Мк = 200-400 = -200 Нм;
В
сечении с-с на участке СD
Мк
= 200-400-600 + 100z,
0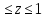 м.
м.
В сечении d-d на участке DE Мк = 200-400-600+100+200= - 500 Нм;
Эпюра крутящих моментов имеет форму прямоугольников, за исключением участка, на котором приложен распределенный крутящий момент. Следует отметить, что в том сечении, где имеется сосредоточенный крутящий момент ордината эпюры скачкообразно изменяется на величину приложенного здесь момента.
4)Определение напряжений и деформаций при кручении вала круглого сечения.


-
Кручение вала прямоугольного сечения