Файл: Теория.docx

Раздел 9. Сложные виды сопротивления.

Сложное сопротивление – одновременное действие на брус нескольких простых видов деформаций: растяжения-сжатия, сдвига, кручения и изгиба.

Виды сложного сопротивления:

1. Кручение с изгибом. Сочетание деформаций изгиба и кручения.

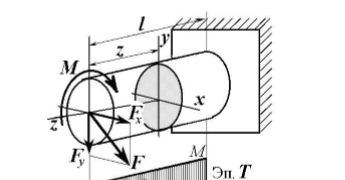
2. Косой изгиб.

При плоском косом изгибе внешняя нагрузка, приложенная к стержню, лежит в одной плоскости, но она не совпадает ни с одной из главных плоскостей стержня.

В этом случае сам стержень будет изгибаться в плоскости, не совпадающей с плоскостью действия нагрузки, то есть косо по отношению к не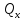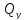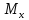й (, , и 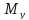– 4 ВСФ).

При пространственном изгибе внешняя нагрузка, приложенная к стержню, лежит одновременно в двух и более плоскостях (, , 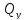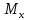и 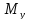– 4 ВСФ).

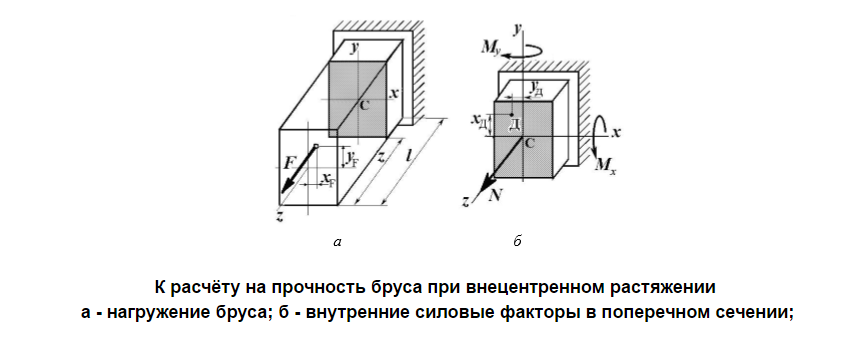
3. Внецентренное растяжение (сжатие). При таком виде сложного сопротивления продольная сила приложена не в центре тяжести поперечного сечения бруса (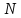, 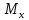и ).

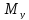Раздел 10. Усталостная прочность материалов.

Усталостью материалов называется процесс образования и развития трещин под действием периодически меняющейся нагрузки.

Различают малоцикловую усталость, при которой наблюдаются заметные деформации, а число циклов до разрешения не превышает 50000 циклов, и многоцикловую усталость, при которой уровень напряжений может быть значительно ниже пределов упругости или текучести, а число циклов до разрушения составляет от сотен тысяч до десятков миллионов циклов.

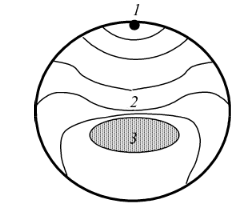
При усталостном разрушении на поверхности излома можно выделить три характерные зоны: зону зарождения трещины 1, имеющую вид темного пятна, зону её развития 2, занимающую, как правило, большую часть площади излома и представляющую гладкую поверхность, и так называемую зону долома 3 с зернистой структурой.

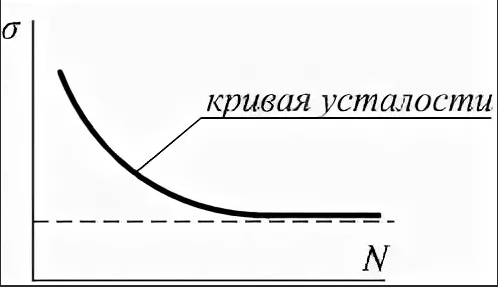
Кривая усталости (кривая Велера) – это график зависимости напряжений, при котором происходит разрушение материала при данном числе циклов нагружения, от числа этих циклов.

Циклическая долговечность – число циклов напряжения или деформаций, которое выдерживает нагруженный объект до образования усталостной трещины определённой протяженности или до усталостного разрушения.

Предел выносливости – максимальное напряжение цикла, которое выдерживает материал, не разрушаясь при достаточно большом числе повторно-переменных нагружений (циклов).

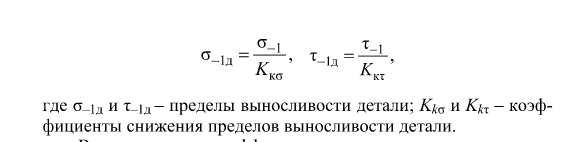
Основными показателями местных напряжений являются теоретические коэффициенты концентрации напряжений.

Для нормальных напряжений

Раздел 11. Устойчивость сжатых стержней.

Продольный изгиб – изгиб длинномерных стержней, под воздействием осевой сжимающей силы.

Виды равновесия системы:

1. Устойчивое равновесие.

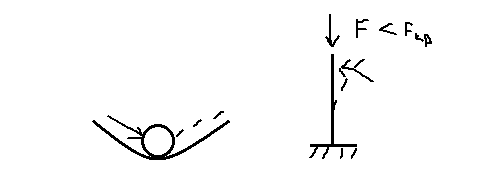
После снятия внешнего воздействия система возвращается в исходное состояние.

2. Неустойчивое равновесие.

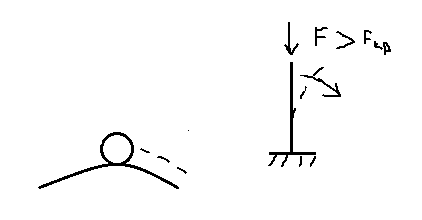
После снятия внешнего воздействия система не возвращается в исходное состояние.

3. Промежуточное (безразличное) равновесие.

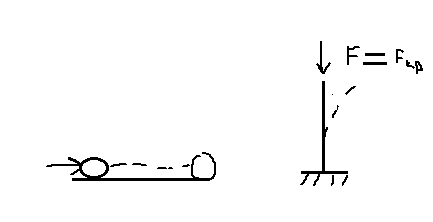
После снятия внешнего воздействия система не возвращается в исходное состояние, но в новом состоянии она так же находится в равновесии.

Критическая сила сжатого стержня – наименьшее значение сжимающего усилия, при котором возможна потеря устойчивости.

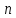– количество полуволн и синусоиды, которое приобретает изогнутая ось балки при потере устойчивости.

Коэффициент запаса – величина, показывающая способность конструкции выдерживать прилагаемые к ней нагрузки выше расчётных. Наличие запаса прочности обеспечивает дополнительную надёжность конструкции, чтобы избежать катастрофы в случае возможных ошибок проектирования, изготовления или эксплуатации.

Гибкость стержня – отношение расчётной длины стержня к наименьшему радиусу инерции его поперечного сечения:

.

Вопросы категории 3. Выведите зависимости, описывающие…

Раздел 1. Основные понятия, гипотезы и принципы.

Метод сечений позволяет определить внутренние силы, которые возникают в стержне, находящемся в равновесии под действием внешней нагрузки.

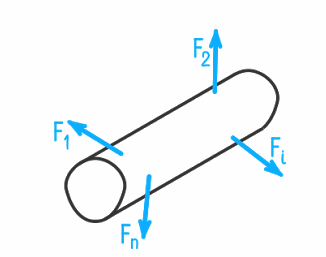
Надо рассечь брус, находящийся в равновесии, на две части и рассмотреть равновесие одной из них.

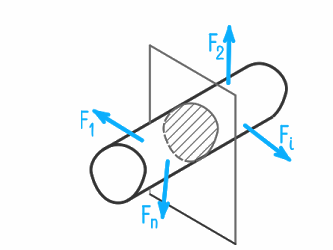
Действие усилий отброшенной части бруса заменим уравновешивающими рассматриваемую часть внутренней силой 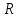и внутренним моментом .

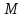Для упрощения расчётов силу 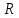и момент 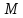принято раскладывать на составляющие усилия относительно осей координат 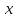, 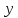и .

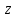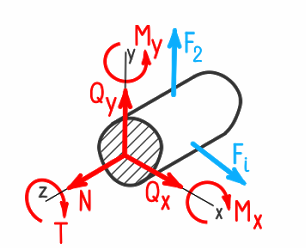
Таким образом, под действием внешних нагрузок в поперечном сечении бруса могут возникать следующие внутренние силовые факторы:

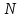• – продольная сила;

•  – крутящий (скручивающий) момент;

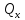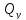• ,  – поперечные силы;

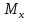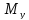• , – изгибающие моменты.

Каждый внутренний силовой фактор определяется из соответствующего уравнения равновесия оставшейся после рассечения бруса части.

При поперечном изгибе в сечении стержня одновременно возникают поперечная сила и изгибающий момент

Деформация – это геометрическое искажение в окрестности материальной точки. Деформация тоже подразделяется на линейную и угловую. Для определения деформации в точке 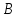рассмотрим два малых отрезка 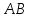и 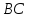, выделенных в теле до его деформации и после нагружения.

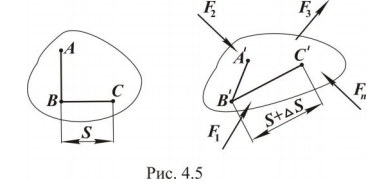
После приложения нагрузки отрезки изменяют свою длину и взаимный угол расположения. При этом

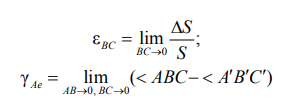
будут являться соответственно линейной и угловой деформацией в точке .

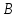Раздел 2. Растяжение и сжатие.

Закон Гука при растяжении и сжатии справедлив лишь в определённых пределах нагружения и формулируется так: нормальное напряжение прямо пропорционально относительному удлинению или укорочению.

Математически закон Гука можно записать в виде равенства:

.

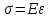Коэффициент пропорциональности 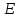 характеризует жёст­кость материала, т. е. его способность сопротивляться упругим деформациям растяжения или сжатия, и называется модулем продольной упругости или модулем упругости первого рода.

Если в формулу закона Гука подставим выражения

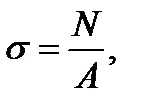
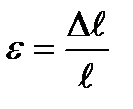
то получим

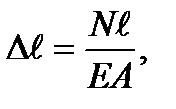
Произведение 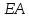, стоящее в знаменателе, называется жёсткостью сечения при растяжении и сжатии; оно характеризует одновременно физико-механические свойства ма­териала и геометрические размеры поперечного сечения бруса.

Для бруса, имеющего несколько участков, отличающихся материалом, размерами поперечного сечения, продольной силой, изменение длины всего бруса равно алгебраической сумме удлинений и укорочений отдельных участков: