Файл: Теория.docx

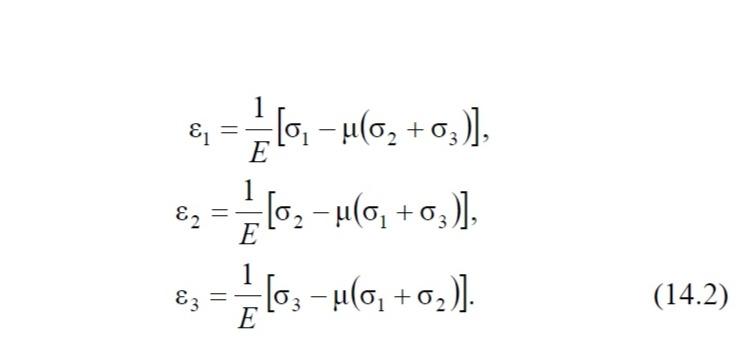
Выражения (14.2) представляют собой обобщенный закон Гука для главных деформаций. Поскольку деформации принимаются малыми, влиянием сдвигов на линейные деформации можно пренебречь и считать формулы (14.2) справедливыми не только для главных деформаций, но и для линейных деформаций по любым трем взаимно перпендикулярным направлениям. В этом случае обобщенный закон Гука необходимо дополнить выражениями для углов сдвига:

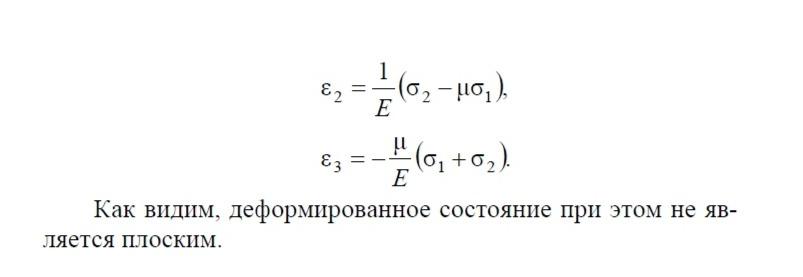
• назначение и суть теорий прочности, эквивалентное напряжение

Теории прочности

Одной из главных задач инженерного расчёта является оценка прочности конструкции по известному напряжённому состоянию. В случае простых видов нагружения опасные напряжения, при которых конструкция переходит в предельное состояние, легко находятся экспериментально. Так, если напряжённое состояние в элементе конструкции является одноосным, переход в предельное состояние происходит тогда, когда нормальное напряжение достигает предела текучести в пластичном материале или предела прочности в хрупком. В случае плоского или объёмного напряжённого состояния ситуация существенно усложняется. Очевидный на первый взгляд путь экспериментального исследования прочности образцов при соответствующем нагружении приходится отклонить. Это объясняется как неоправданным усложнением испытательного оборудования, так и необходимостью проведения бесчисленного множества экспериментов, поскольку для каждой новой комбинации нормальных и касательных напряжений испытания пришлось бы проводить заново. В связи с этим представляется заманчивым найти такой критерий прочности, при достижении которого сложное напряжённое состояние становится предельным. Существуют различные теории о преимущественном влиянии на прочность того или иного фактора, который и принимается в качестве соответствующего критерия прочности. Все они используют понятие равнопрочности, которое можно сформулировать следующим образом: два различных напряжённых состояния считаются равнопрочными (равноопасными), если при пропорциональном увеличении их главных напряжений в одно и то же число раз, они одновременно становятся предельными. Число, на которое умножаются главные напряжения для перехода в предельное состояние, представляет собой не что иное, как коэффициент запаса прочности.

Предельное значение фактора, определяющего прочность, легко находится на основании стандартных опытов на растяжение и сжатие. Критерий прочности позволяет сопоставить исследуемое сложное напряжённое состояние с простым, например, осевым растяжением, и установить эквивалентное (равноопасное) напряжение в растянутом стержне с таким же коэффициентом запаса (рис. 14.4).

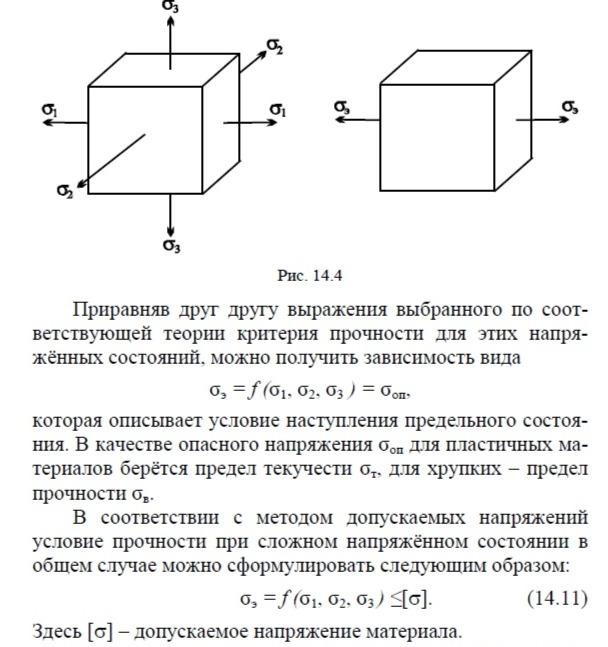
Различные теории прочности приводят к различным выражениям для эквивалентного напряжения. Наличие нескольких теорий не должно вызывать удивления, поскольку каждый из критериев прочности (наибольшее нормальное напряжение, наибольшая линейная деформация, потенциальная энергия деформации и т. д.) лишь отчасти отражает весьма сложный процесс наступления предельного состояния и применим только в определённых условиях. Далее мы познакомимся с наиболее простыми, классическими теориями прочности.

• классические теории прочности

ного состояния в основном определяется величиной наибольшего σ1 и наименьшего σ3, главных напряжений, и в гораздо меньшей степени зависит от напряжения σ2. Поэтому при оценке прочности из трёх кругов можно использовать только наибольший, который называют главным кругом. Если при этом напряжения σ1 и σ3 таковы, что напряжённое состояние является предельным, соответствующий им главный круг также называют предельным кругом.

Получив на основе испытаний при различных соотношениях между главными напряжениями семейство предельных кругов, можно построить их огибающую, которая называется предельной огибающей. Она представляет собой кривую, пересекающую горизонтальную ось в точке C, соответствующей всестороннему растяжению. Многие материалы при сжатии выдерживают гораздо большие напряжения, чем при растяжении, поэтому диаметры показанных на рис. 14.6 предельных кругов увеличиваются по мере продвижения в область отрицательных нормальных напряжений. Слева предельная огибающая оказывается незамкнутой, поскольку при всестороннем сжатии материал способен выдержать, не разрушаясь, чрезвычайно большие нагрузки.

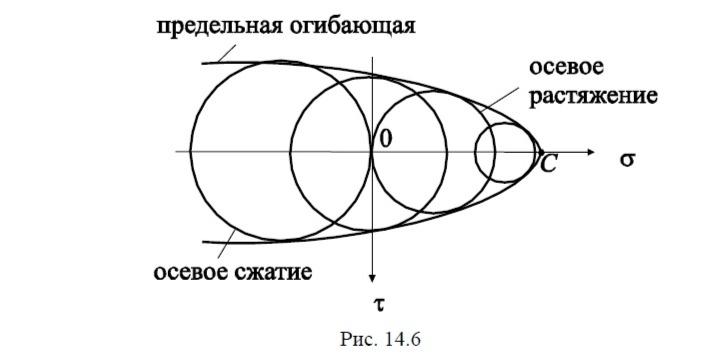
Если главный круг, соответствующий напряжённому состоянию в опасной точке конструкции, лежит внутри предельной огибающей, то можно считать, что прочность обеспечена. При этом отношение диаметров предельного и найденного главного кругов представляет собой коэффициент запаса прочности. Проблема состоит лишь в том, что построение предельной огибающей для всей области возможных сочетаний напряжений на практике неосуществимо. Поэтому действительную огибающую схематизируют, заменяя прямыми, касательными к двум предельным кругам, соответствующим осевому растяжению и осевому сжатию, как это показано на рис. 14.7

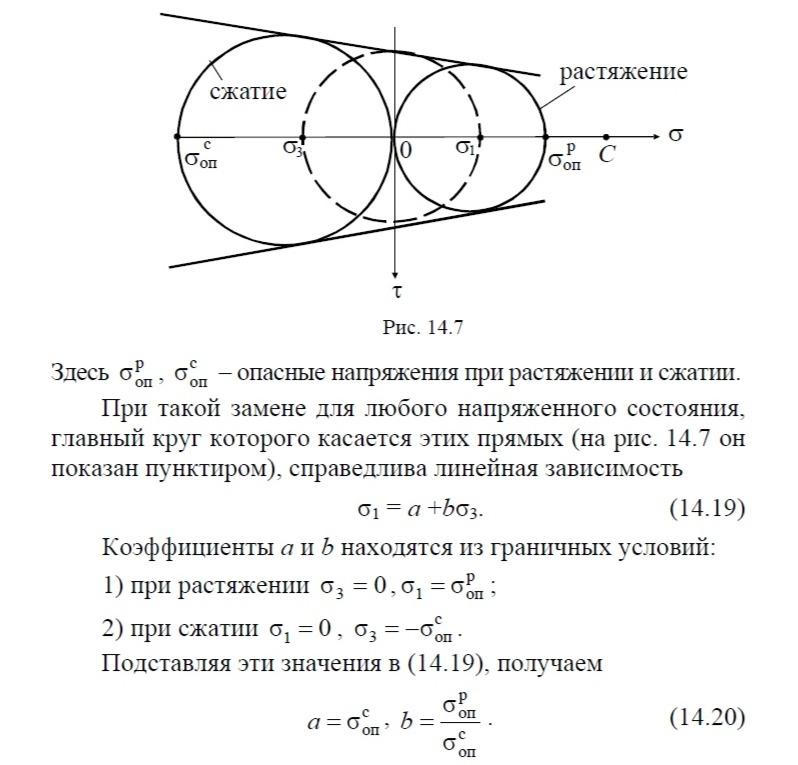
Раздел 9. Сложные виды сопротивления

Сложными называют такие виды нагружения, при которых в поперечных сечениях стержня одновременно возникает несколько внутренних силовых факторов. В такой ситуации говорят о сложном сопротивлении, понимая под ним различные комбинации уже рассмотренных нами ранее простых видов нагружения. Возникающие при этом деформации считаются достаточно малыми, что позволяет применить принцип независимости действия сил. Из существующего разнообразия видов сложного нагружения в инженерной практике наиболее часто встречаются следующие:

• косой изгиб;

• внецентренное растяжение (сжатие);

• совместное действие изгиба с кручением.

• внутренние силовые факторы и напряжения при косом изгибе

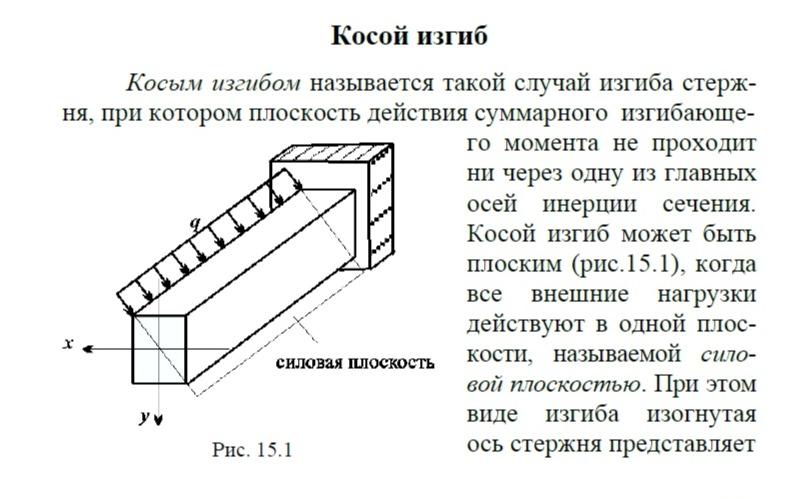
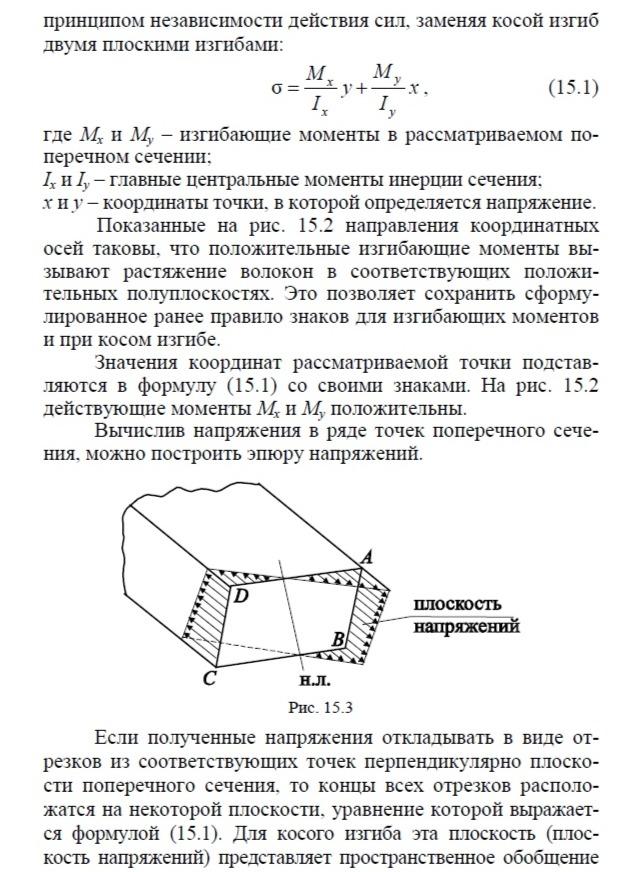
эпюры напряжений, изображаемой для плоского изгиба прямой линией. Примерный вид плоскости напряжений показан на рис. 15.3.

внутренние силовые факторы и напряжения при внецентренном растяжении (сжатии)

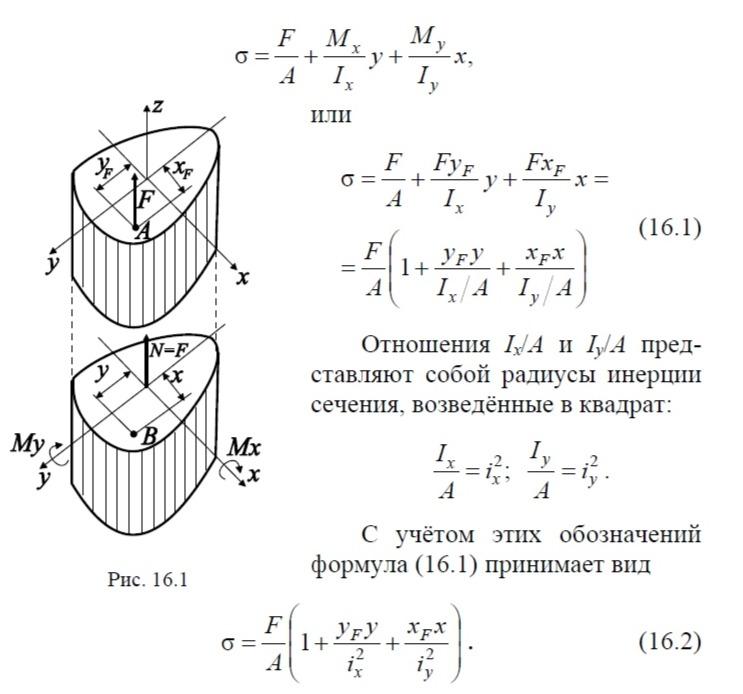
При определении напряжений по формуле (16.2) величины x_F, х, y_F, у берутся с учётом их знака относительно координатных осей. Кроме того, в условиях внецентренного сжатия перед правой частью формулы (16.2) ставится знак минус.

При сложном профиле сечения стержня для определения опасной точки предварительно находится положение нейтральной линии. Учитывая, что на нейтральной линии напряжения равны нулю, получаем

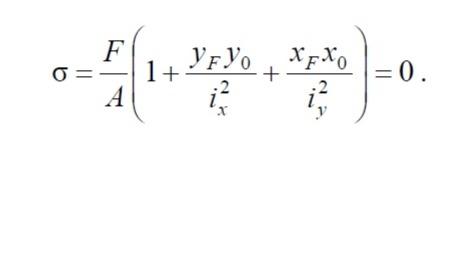
• внутренние силовые факторы и напряжения при изгибе с кручением

Раздел 10. Усталостная прочность материалов

Явление усталости

Усталостью материалов называется процесс образования и развития трещин под действием периодически меняющейся нагрузки.

Различают малоцикловую усталость, при которой наблюдаются заметные пластические деформации, а число циклов до разрушения не превышает 50000 циклов, и многоцикловую усталость, при которой уровень напряжений может быть значительно ниже пределов упругости или текучести, а число циклов до разрушения составляет от сотен тысяч до десятков миллионов циклов. Но и в этом случае из-за существенной микронеоднородности современных конструкционных материалов зарождение трещины усталости связано с локальными повторными пластическими деформациями, протекающими в отдельных структурных элементах материала.

• характеристики циклов напряжений

Под действием периодически меняющихся нагрузок в опасной точке возникают так же периодически меняющиеся напряжения. Пусть в некоторой детали реализуется линейное напряженное состояние, а нормальные напряжения в опасном сечении во времени меняются по закону, показанному на рис.18.2. Время, через которое значения напряжений полностью повторяются, называется периодом Т. Совокупность значений напряжений за период составляет цикл напряжений. С точки зрения усталости в большинстве случаев для характеристики цикла достаточно знать максимальное σ_max и минимальное σ_min значения напряжений в цикле.

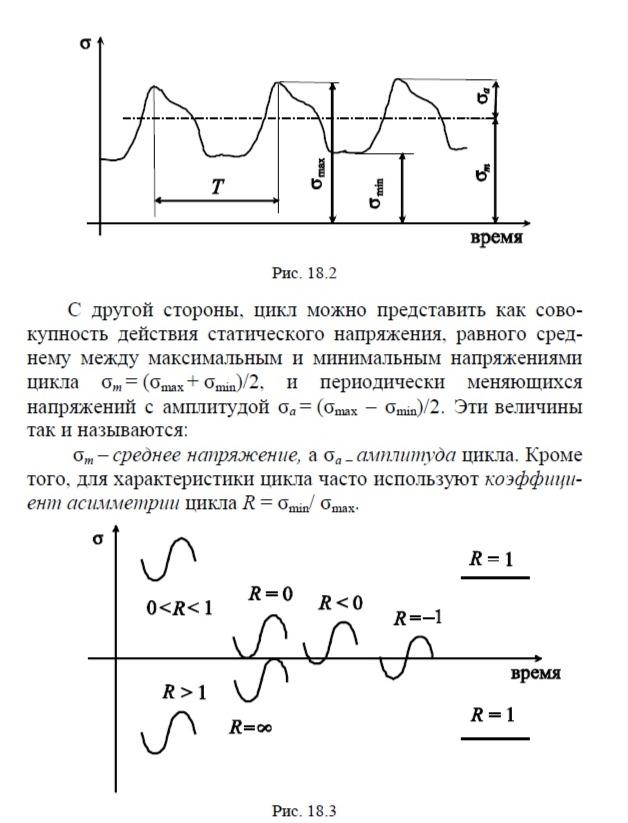
В зависимости от знака и значения коэффициента асимметрии циклы подразделяются на знакопостоянные – R > 0, и знакопеременные – R < 0. Если R = 0 цикл называется положительным отнулевым, если

Примеры различных видов цикла приведены на рис. 18.3.

R = ∞ – отрицательным отнулевым, при R = –1 цикл называется симметричным, а при R = 1 цикл вырождается в постоянно действующее напряжение.

• характеристики сопротивления усталости

Механические характеристики сопротивления усталости определяются путем испытаний образцов на специальных усталостных машинах. Требования к образцам и испытательным машинам, методики проведения испытаний и обработки их результатов строго регламентируются ГОСТом.