ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 27.03.2024
Просмотров: 98
Скачиваний: 0
СОДЕРЖАНИЕ
Вопросы категории 1. Что в разделе «…» обозначается как «…»?
Раздел 1. Основные понятия, гипотезы и принципы.
Раздел 2. Растяжение и сжатие.
Раздел 3. Механические свойства конструкционных материалов.
Раздел 4. Геометрические характеристики плоских сечений.
Раздел 6. Изгиб прямого стержня.
Раздел 7. Перемещения при изгибе.
Раздел 8. Основы теории напряжённого и деформированного состояния в точке тела.
Раздел 9. Сложные виды сопротивления
Раздел 10. Усталостная прочность материалов.
Раздел 11. Устойчивость сжатых стержней.
Раздел 1. Основные понятия, гипотезы и принципы.
Какие виды деформации бруса определяют внутренние силовые факторы ?
Раздел 2. Растяжение и сжатие.
Раздел 3. Механические свойства конструкционных материалов
Раздел 4. Геометрические характеристики плоских сечений.
Раздел 6. Изгиб прямого сечения.
Раздел 7. Перемещения при изгибе.
Раздел 8. Основы теории напряжённого и деформированного состояния в точке.
Раздел 9. Сложные виды сопротивления.
Раздел 10. Усталостная прочность материалов.
Раздел 11. Устойчивость сжатых стержней.
Вопросы категории 3. Выведите зависимости, описывающие…
Раздел 1. Основные понятия, гипотезы и принципы.
Раздел 2. Растяжение и сжатие.
Раздел 3. Механические свойства конструкционных материалов.
Раздел 4. Геометрические характеристики плоских сечений.
Раздел 5. Изгиб прямого стержня.
Раздел 7. Перемещения при изгибе
Раздел 8. Основы теории напряженного и деформированного состояния в точке
Раздел 9. Сложные виды сопротивления
Раздел 10. Усталостная прочность материалов
Раздел 11. Устойчивость сжатых стержней
Дать определение основным видам изгиба.
Какие внутренние силовые факторы возникают в сечении бруса при деформации изгиба ?
Назвать геометрические характеристики плоских сечений и их размерности.
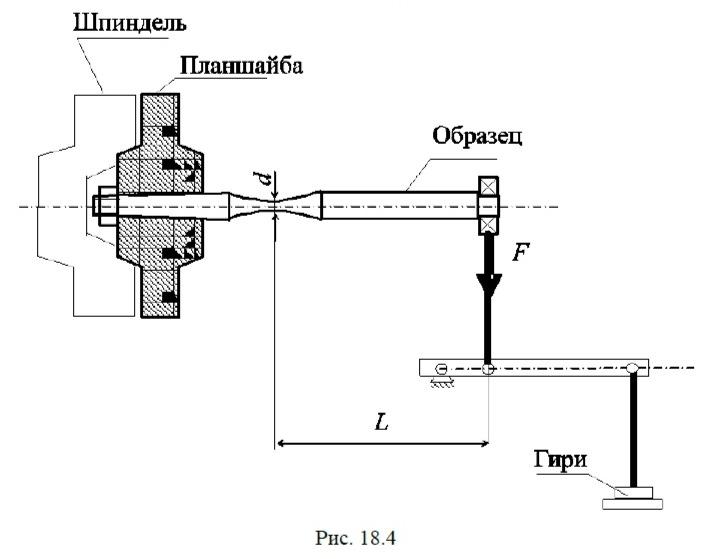
Усталостные машины отличаются по виду нагружения (осевое растяжение-сжатие, изгиб вращающегося образца, плоский изгиб, кручение, комбинированное нагружение и т. д.), по способу силовозбуждения (механическое, гидравлическое, резонансное и т. д.). На рис. 18.4 показана схема простейшей механической усталостной машины, осуществляющей изгиб вращающегося образца. Машина позволяет проводить испытания при симметричных циклах нагружения, наиболее часто применяемых на практике.

Испытывается серия одинаковых образцов в количестве не менее 10 штук. Первый образец устанавливается на достаточно большом уровне напряжений σ1, и фиксируется число циклов до разрушения (долговечность) N1. Для следующих образцов уровни напряжений последовательно снижаются и определяются их долговечности. В результате испытаний серии образцов получают уровни максимальных напряжений цикла σmax и соответствующие им долговечности N.
Результаты испытаний наносят на график, откладывая по оси абсцисс долговечности, а по оси ординат максимальные напряжения цикла. Так как долговечности в одной серии испытаний могут отличаться в сотни и тысячи раз, по оси абсцисс обычно используют логарифмическую шкалу, а по оси ординат как логарифмическую, так и равномерную шкалы.
График зависимости долговечность – максимальное напряжение цикла при фиксированном коэффициенте асимметрии цикла носит название кривой усталости, которая, по существу, и является характеристикой сопротивления усталости.
На рис.18.5 показаны два типичных вида кривых усталости.
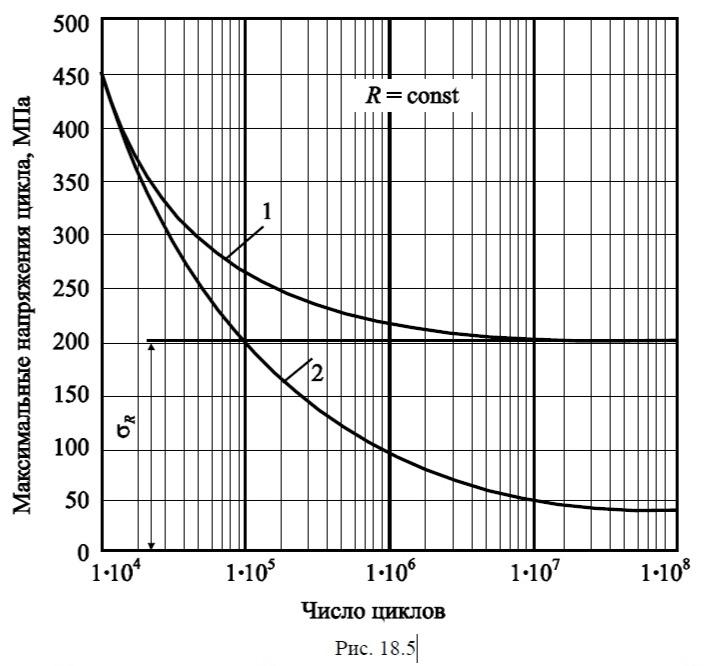
Для кривых вида 1 характерно наличие горизонтальной асимптоты, т. е. наибольшего максимального напряжения цикла, при котором разрушение не наступает за сколь угодно большое число циклов. Такое максимальное напряжение цикла носит название физического предела выносливости и обозначается σR, где индекс R равен коэффициенту асимметрии, при котором проводились испытания. Например σ-1, σ0, σ0,1 и т. д. Такими кривыми обладают в основном мало-углеродистые стали. Число циклов нагружения, по достижении которого дальнейшие испытания прекращаются, носит название базы испытаний – N0. ГОСТом рекомендуется принимать N0 = 107 циклов.
Кривые типа 2 характерны для цветных металлов и сплавов и некоторых легированных сталей. В этом случае определяется так называемый условный предел выносливости, т. е. такое наибольшее максимальное напряжение цикла, при котором разрушение наступает за количество циклов, равное базе. При этом база испытаний увеличивается до 108 циклов и более. Условные пределы выносливости обозначаются так же, как и физические, но при этом указывается база испытаний.
Пределы выносливости являются основными механическими характеристиками сопротивления усталости. Так как результаты усталостных испытаний очень чувствительны к конструктивным, технологическим и внешним факторам, принято определять пределы выносливости на гладких полированных образцах диаметром 8…12 мм при комнатной температуре в сухой воздушной среде. Чаще всего проводят испытания при R = – 1, т. е. определяют σ-1.
конструктивно-технологические факторы, влияющие на усталостную прочность
Влияние конструкционных факторов
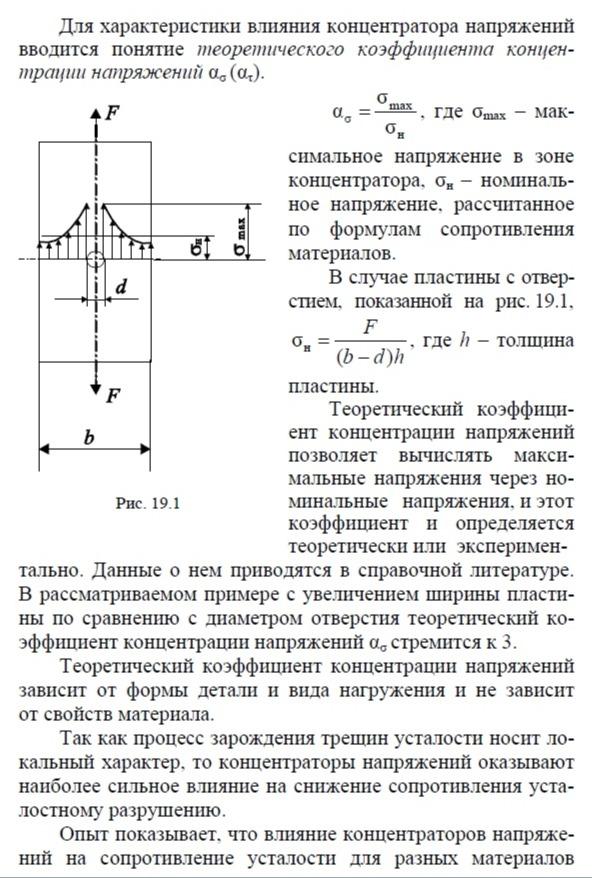
Детали машин обычно имеют достаточно сложную форму из-за наличия различных конструкционных элементов: галтельных переходов, шпоночных канавок, выточек, шлицов, отверстий и т.п. Теоретически и экспериментально установлено, что в местах резкого изменения размеров и формы детали происходит локальное повышение напряжений, при этом напряженное состояние становится, как правило, более сложным. Это явление, как уже было сказано, называется концентрацией напряжений, а геометрический фактор, вызывающий это повышение, – концентратором. Влияние концентраторов на напряженное состояние весьма значительно. На рис. 19.1 в качестве примера показано распределение нормальных напряжений в пластине с круглым отверстием, растягиваемой осевой нагрузкой F.

Влияние качества поверхности на сопротивление усталости
Как уже отмечалось, усталостное разрушение почти всегда начинается с поверхности, точнее в приповерхностном слое. В связи с этим становится понятным существенное влияние состояние этого слоя на сопротивление усталости. При изготовлении детали именно приповерхностный слой подвержен различного рода воздействиям, могущим существенно изменить свойства этого слоя как в лучшую, так и в худшую стороны.
Одним из основных факторов, влияющих на свойства слоя, является геометрический фактор. Чем выше шероховатость поверхности, тем эффективнее микроконцентраторы напряжений, представляющих собой чередование выступов и впадин профиля поверхности, и, соответственно, ниже предел выносливости. Кроме того, на предел выносливости оказывают влияние и другие факторы, такие как наклеп, наведение в процессе обработки остаточных напряжений, обезуглероживание приповерхностного слоя, или насыщение его какими-либо элементами и т. д.

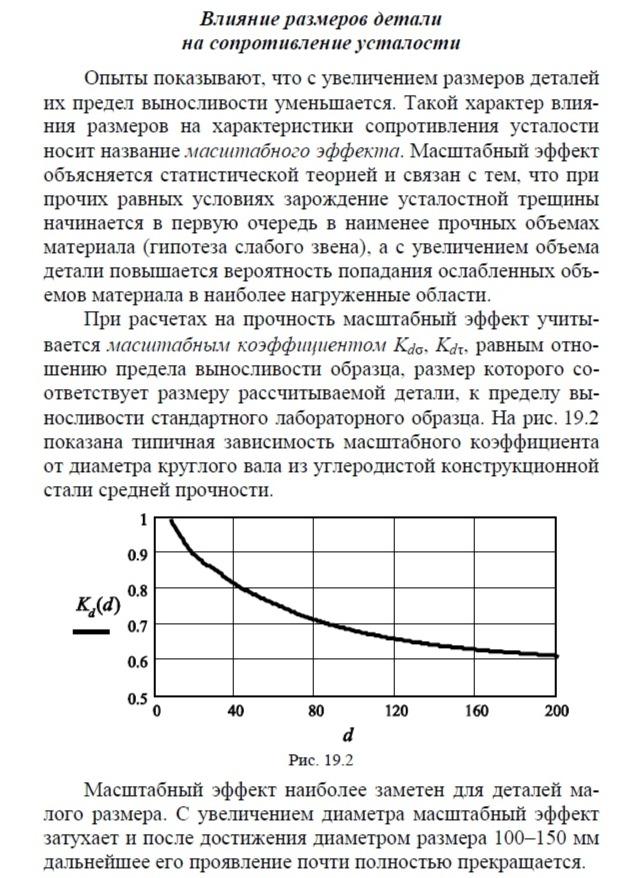
Раздел 11. Устойчивость сжатых стержней
-
формула Эйлера для определения критической силы сжатого стержня
Рассмотрим шарнирно опёртый центрально сжатый стержень постоянного сечения (рис. 21.2). Будем считать, что сжимающая сила достигла своего критического значения и стержень сохраняет устойчивое равновесие как в прямолинейной, так и в деформированной, т. е. изогнутой форме. В этом случае в произвольном поперечном сечении стержня возникает изгибающий момент



-
влияние условий закрепления стержня на величину критической силы
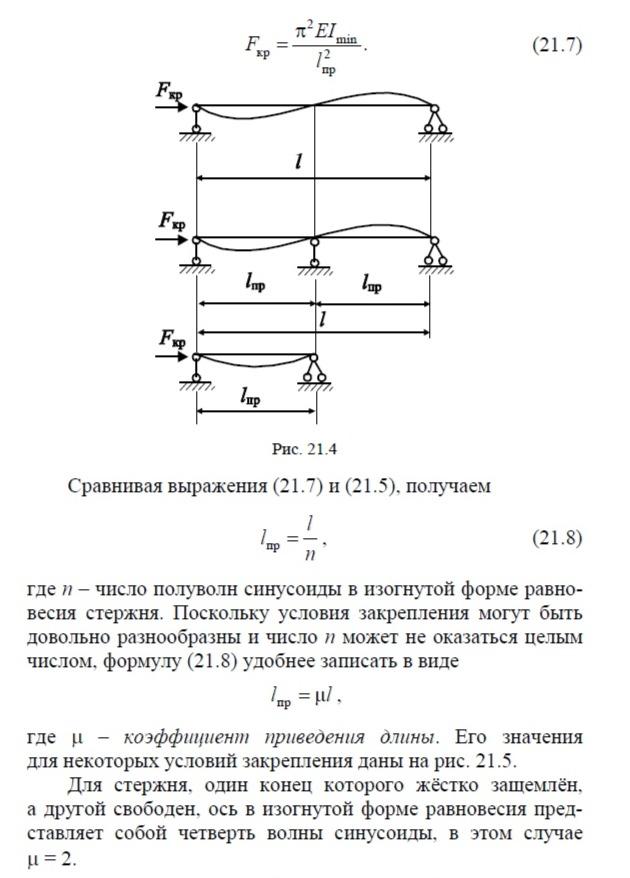
Формулу Эйлера, полученную для шарнирно опёртого стержня, можно обобщить и на другие способы закрепления. Легко увидеть, что у стержней, показанных на рис. 21.4, критическая сила совпадает. При любых условиях закрепления можно выделить ту часть длины стержня, на которой прогибы имеют форму полуволны синусоиды. Эта часть стержня называется приведённой длиной и обозначается lпр (рис. 21.4).
Её можно трактовать как условную длину некоторого шарнирно опёртого стержня с такой же критической силой, как у исследуемого стержня с другими условиями закрепления. Тогда формулу Эйлера для стержня с произвольными граничными условиями можно записать следующим образом:
Для стержня, защемлённого по концам, в изогнутой форме имеем две полуволны – одну в центральной части стержня и две четверти полуволны по краям, т. е. μ = 0,5.
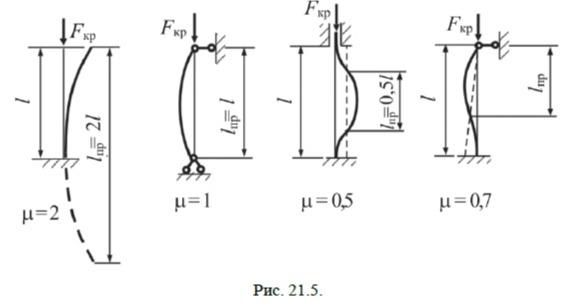
Для стержня, один конец которого защемлён, а другой закреплён шарнирно, число полуволн оказывается дробным: п ≈ 1,5, в этом случае μ = 0,7.
Пользуясь изложенной методикой, несложно определить приведённую длину и при других условиях закрепления. При этом необходимо учитывать, что условия закрепления в разных плоскостях могут быть различны. В таких случаях критическая сила в каждой из плоскостей должна вычисляться отдельно, а в качестве окончательного значения принимается наименьшее из полученных значений.
-
критические напряжения
-
пределы применимости формулы Эйлера
Формула Эйлера получена на основе решения дифференциального уравнения изогнутой оси стержня, которое, в свою очередь, предполагает, что материал подчиняется закону Гука. Таким образом, формула Эйлера оказывается справедливой лишь до тех пор, пока величина нормальных напряжений, вызванных сжимающей силой, не превышает предела пропорциональности материала. Введём понятие критических напряжений, т. е. напряжений, возникающих в поперечном сечении от действия критической силы:

 пре
пре
-
расчет на устойчивость за пределом пропорциональности
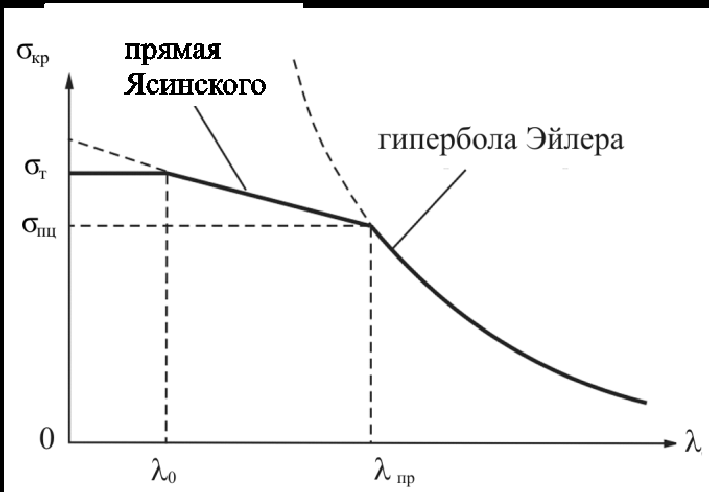
Рис. 21.6
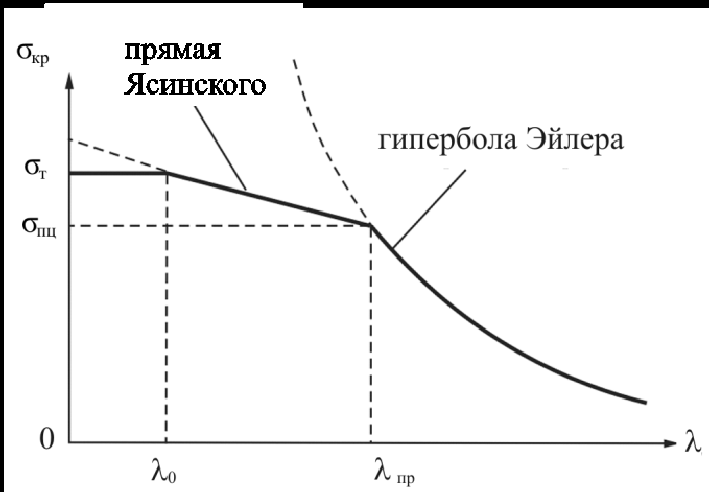
На рис. 21.6 зависимость (21.12) имеет вид наклонной прямой.
Разрушение коротких жёстких стержней (λ<λ0) происходит без потери устойчивости, для них ограничиваются расчётом на прочность. Для большинства конструкционных материалов значения λ0, λпр, как и значения коэффициентов a, b, имеются в справочниках по сопротивлению материалов. Для углеродистых сталей, например, λ0 = 40…60.
Диаграмму, приведённую на рис. 21.6, обычно называют полным графиком критических напряжений.
Пример. Найти коэффициент запаса по устойчивости для стальной стойки, изготовленной из швеллера № 18 (рис. 21.7).
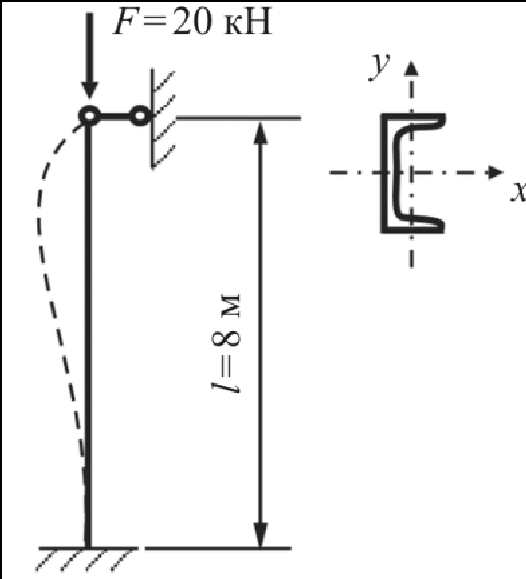
Рис. 21. 7
Решение. Для выбора расчётной формулы сначала определим гибкость стойки. Минимальным радиусом инерции для швеллера будет величина iу = 2, 04 см.
Принимая коэффициент приведения длины равным 0,7, получаем

-
полный график критических напряжений