ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 27.03.2024
Просмотров: 122
Скачиваний: 0
СОДЕРЖАНИЕ
Вопросы категории 1. Что в разделе «…» обозначается как «…»?
Раздел 1. Основные понятия, гипотезы и принципы.
Раздел 2. Растяжение и сжатие.
Раздел 3. Механические свойства конструкционных материалов.
Раздел 4. Геометрические характеристики плоских сечений.
Раздел 6. Изгиб прямого стержня.
Раздел 7. Перемещения при изгибе.
Раздел 8. Основы теории напряжённого и деформированного состояния в точке тела.
Раздел 9. Сложные виды сопротивления
Раздел 10. Усталостная прочность материалов.
Раздел 11. Устойчивость сжатых стержней.
Раздел 1. Основные понятия, гипотезы и принципы.
Какие виды деформации бруса определяют внутренние силовые факторы ?
Раздел 2. Растяжение и сжатие.
Раздел 3. Механические свойства конструкционных материалов
Раздел 4. Геометрические характеристики плоских сечений.
Раздел 6. Изгиб прямого сечения.
Раздел 7. Перемещения при изгибе.
Раздел 8. Основы теории напряжённого и деформированного состояния в точке.
Раздел 9. Сложные виды сопротивления.
Раздел 10. Усталостная прочность материалов.
Раздел 11. Устойчивость сжатых стержней.
Вопросы категории 3. Выведите зависимости, описывающие…
Раздел 1. Основные понятия, гипотезы и принципы.
Раздел 2. Растяжение и сжатие.
Раздел 3. Механические свойства конструкционных материалов.
Раздел 4. Геометрические характеристики плоских сечений.
Раздел 5. Изгиб прямого стержня.
Раздел 7. Перемещения при изгибе
Раздел 8. Основы теории напряженного и деформированного состояния в точке
Раздел 9. Сложные виды сопротивления
Раздел 10. Усталостная прочность материалов
Раздел 11. Устойчивость сжатых стержней
Дать определение основным видам изгиба.
Какие внутренние силовые факторы возникают в сечении бруса при деформации изгиба ?
Назвать геометрические характеристики плоских сечений и их размерности.
Раздел 5. Изгиб прямого стержня.
-
дифференциальные зависимости при изгибе
Между внутренними силовыми факторами при изгибе и внешней распределённой нагрузкой существуют важные дифференциальные зависимости.
Рассмотрим балку, нагруженную распределёнными по её длине вертикальными силами, интенсивность которых q(z) может быть переменной (рис. 6.6).
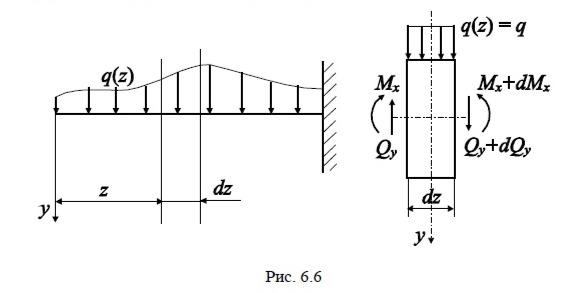
Поскольку большая часть распределенных нагрузок связана с весом, удобнее направить ось y вниз и считать нагрузку такого направления положительной. С помощью двух бесконечно близких поперечных сечений выделим из балки элемент длиной dz. Действие на элемент левой отброшенной части балки заменим поперечной силой Qy и изгибающим моментом Мx, действие правой – поперечной силой Qy + dQy и моментом Mx + dMx. Приращение внутренних усилий dQy и dMx вызваны приращением координаты dz. Ввиду малости элемента действующую на него распределённую нагрузку можно считать равномерной: q(z) = q = const.
Для того, чтобы выделенный элемент находился в равновесии, должны выполняться следующие условия:


-
построение эпюр внутренних силовых факторов в балках (краткий пример)
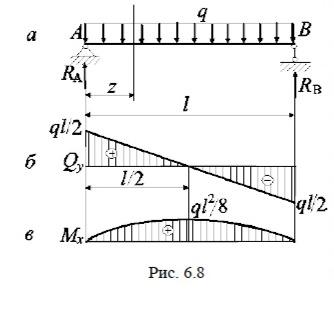
Построение эпюр поперечных сил и изгибающих моментов в балках
Эпюры поперечных сил и изгибающих моментов представляют собой графическое изображение функций Qy(z) и Mx(z) по всей длине балки. Эпюры необходимы для нахождения опасных сечений, а также при определении перемещений в балках. Они строятся по вычисленным значениям внутренних усилий в характерных сечениях – местах приложения нагрузки, установки опор и т. п. При этом положительные значения поперечной силы и моментов откладываются вверх от оси, т. е. эпюры изгибающих моментов строятся со стороны сжатых волокон балки.


-
напряжения в балках при чистом изгибе
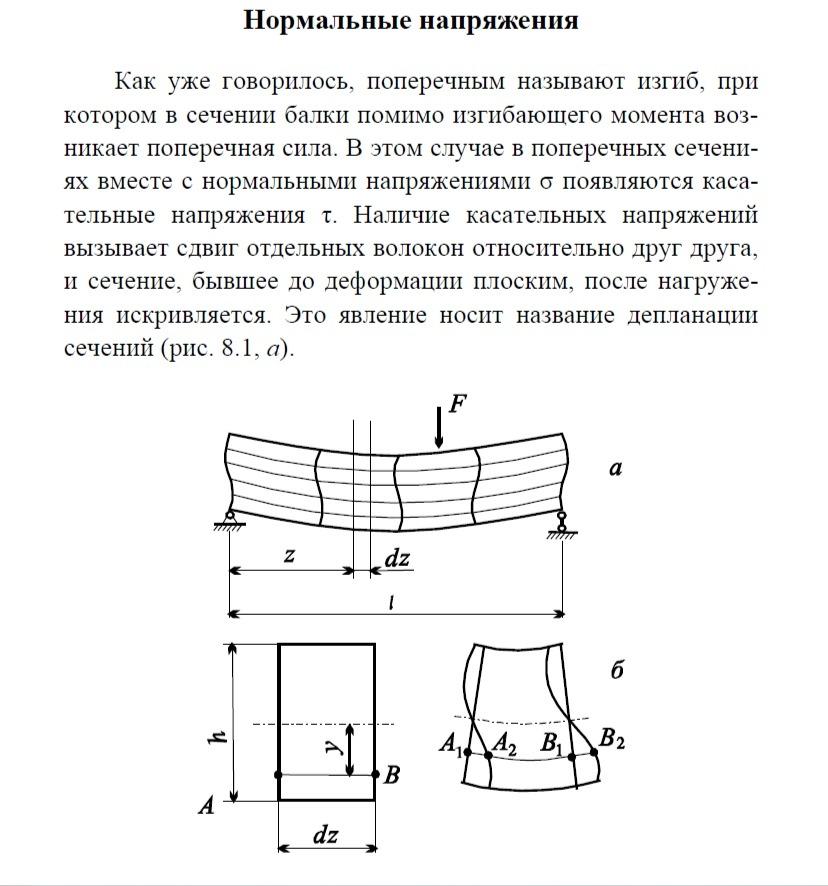
Как отмечалось в самом начале изучения курса «Сопротивление материалов», с помощью метода сечений и уравнений статики можно определить главный вектор и главный момент распределённых по сечению внутренних сил. Но для определения закона, по которому определяются напряжения, одних уравнений равновесия недостаточно – необходимо привлечь условия деформации балки. Здесь на помощь вновь приходят экспериментальные данные. Рассмотрим балку из легко деформирующегося упругого материала (например, поролона), на боковую поверхность которой нанесена сетка из продольных и поперечных прямых. Если подвергнуть такую балку чистому изгибу, то окажется, что продольные линии изогнутся, а поперечные останутся прямыми, повернувшись на некоторый угол (рис. 7.3).
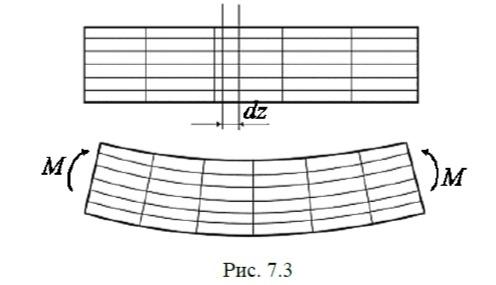
Это обстоятельство, а также некоторые несложные рассуждения приводят к выводу, что при чистом изгибе, как и при осевом растяжении, справедлива гипотеза плоских сечений: поперечные сечения, плоские до нагружения, остаются таковыми и после приложения нагрузки. Таким образом, деформацию при чистом изгибе можно рассматривать как результат взаимного поворота плоских поперечных сечений.
-
кривизна нейтрального слоя
Мысленно вырежем из участка балки, находящегося в состоянии чистого изгиба, бесконечно малый элемент длиной dz (рис. 7.4).
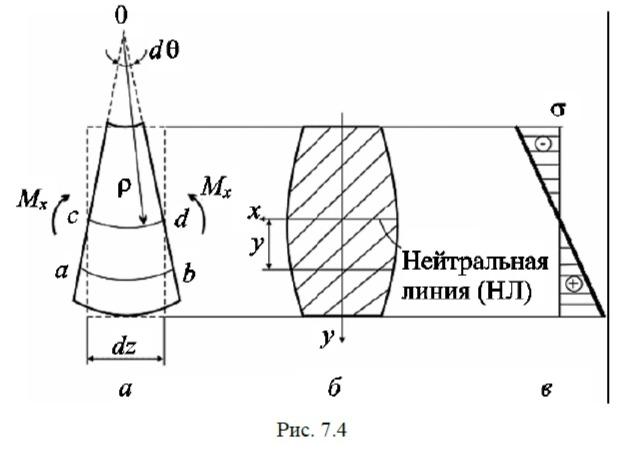
Недеформированное состояние элемента показано пунктиром. После нагружения элемент искривляется. Поперечные сечения, которыми он выделен, поворачиваются в плоскости чертежа на некоторый малый угол dθ. При этом верхние волокна элемента укорачиваются, нижние – растягиваются. Зону сжатия от зоны растяжения будет отделять слой волокон, длина которых остаётся прежней – dz. Этот слой волокон, не меняющий при изгибе своей длины, называют нейтральным слоем, он отмечен на рис. 7.4, а отрезком cd. Пересечение нейтрального слоя с плоскостью поперечного сечения образует прямую, которую называют нейтральной линией (см. рис. 7.4, б). Ось x, проходящая через нейтральную линию, называется нейтральной осью. По ширине балки все волокна деформируются одинаково.
-
условие прочности при чистом изгибе

-
напряжения в балках при поперечном изгибе

-
распределение касательных напряжений по сечению балки (двутавр или др. сечение)



-
полная проверка прочности при изгибе балок тонкостенного профиля
На рис. 8.11, а в качестве примера тонкостенного сечения изображён двутавр с обозначением характерных точек, в которых необходима проверка прочности.

В точках типа 1 (рис. 8.11, а), наиболее удалённых от нейтральной оси, нормальные напряжения достигают максимума, а касательные равны нулю.
Для тонкостенных сечений, так же, как и для сплошных, расчёт на прочность начинают с проверки условия (8.7)
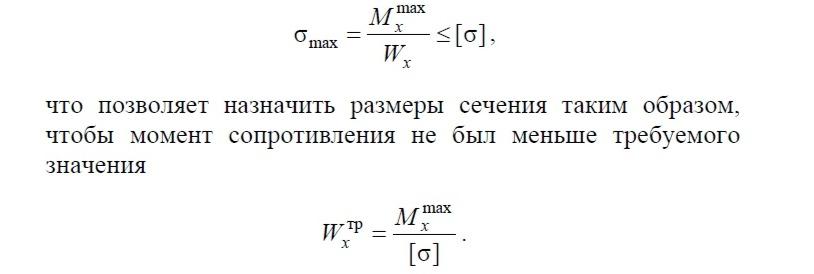
Если для сплошных сечений проверка прочности на этом заканчивается, то для тонкостенных необходим дальнейший расчёт.
В опасных точках типа 2 (см. рис. 8.11, а) возможно разрушение срезом за счёт значительных по величине касательных напряжений. Поскольку нормальных напряжений в этом месте нет, условие прочности имеет вид

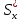 –
статический
момент половины сечения относительно
оси х (для
стандартных профилей приведён в
справочных таблицах);
–
статический
момент половины сечения относительно
оси х (для
стандартных профилей приведён в
справочных таблицах);
d – толщина стойки двутавра.
Если условие прочности по касательным напряжениям не выполняется, необходимо увеличить номер стандартного профиля и повторить расчёт по формуле (8.11). Условие прочности по нормальным напряжениям при этом можно не проверять, поскольку оно заведомо выполняется.
Наконец, необходимо исключить разрушение в опасных точках типа 3, расположенных в местах перехода от полок к стенке. Здесь ни нормальные, ни касательные напряжения не достигают максимума, но имеют значительную величину и действуют совместно. Для проверки прочности в такой ситуации необходимо привлекать так называемые теории прочности, о которых речь пойдет ниже. Пока же приведём условия прочности по наиболее часто применяемым для пластичных материалов третьей и четвёртой теориям:

В
последнюю формулу входит величина
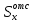 ,
представляющая собой статический момент
полки двутавра относительно оси х.
Полка схематизируется в виде прямоугольника,
размеры которого приведены в справочных
таблицах. Статический момент этой фигуры
легко вычисляется как произведение
площади прямоугольника на расстояние
от его центра тяжести до оси х.
,
представляющая собой статический момент
полки двутавра относительно оси х.
Полка схематизируется в виде прямоугольника,
размеры которого приведены в справочных
таблицах. Статический момент этой фигуры
легко вычисляется как произведение
площади прямоугольника на расстояние
от его центра тяжести до оси х.
Отметим, что обеспечить прочность на этом этапе расчета необходимо для всех сечений, где одновременно велики изгибающий момент и поперечная сила.
Раздел 7. Перемещения при изгибе
-
дифференциальное уравнение изогнутой оси балки
При
рассмотрении нормальных напряжений
при изгибе нами была получена связь
между кривизной балки
 и изгибающим моментом в сечении
и изгибающим моментом в сечении

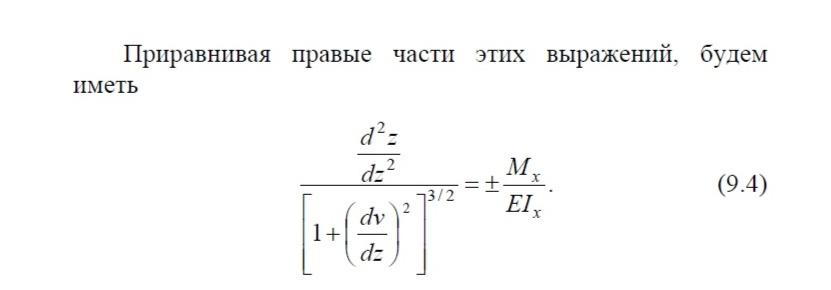
Полученное уравнение называют точным уравнением изогнутой оси балки. Нелинейность этого дифференциального уравнения вызывает значительные трудности при интегрировании. Однако для большинства решаемых практических задач справедливы предположения о малости прогибов и углов, что позволяет исключить нелинейность в (9.4), поскольку стоящая в знаменателе формулы производная


Раздел 8. Основы теории напряженного и деформированного состояния в точке
-
виды напряженного состояния в точке тела
-
Плоское напряженное состояние
Примером конструкции, все точки которой находятся в плоском напряженном состоянии, может служить тонкая пластинка, нагруженная по торцам силами, лежащими в ее плоскости. Поскольку боковые поверхности пластинки свободны от напряжений, то в силу малости ее толщины можно считать, что и внутри пластинки на площадках, параллельных ее поверхности, напряжения пренебрежимо малы. Подобная ситуация возникает, например, при нагружении валов и балок тонкостенного профиля.

-
Объёмная деформация


-
обобщенный закон Гука
При рассмотрении растяжения и сжатия мы выяснили, что линейная деформация в продольном направлении связана с напряжением в поперечном сечении стержня законом Гука:


