Файл: Тестирующая система.doc

Этих методов всего пять. Первый из них называется методом сходства.

1.Метод сходства заключается в том, что при различных наборах обстоятельств проявляется некоторое свойство. Мы в этих различных наборах выделяем сходство в отношении некоторого обстоятельства. Оно-то, очевидно, и является причиной, вызывающей данное свойство.

Схематически это выглядит так:

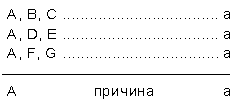
2.Метод различия:

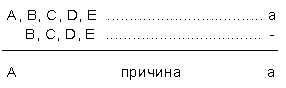
3.Соединенный метод сходства и различия:

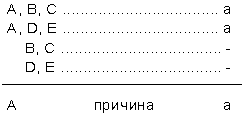
4.Метод остатков:

5.Метод сопутствующих изменений:

Изменение А есть причина изменения а.

Например, надо установить, какой из параметров: температура, давление и, допустим, атомный вес вещества влияют на электропроводность. Для этого можно менять температуру при неизменном давлении (атомный вес, понятно, остается постоянным), и при этом, соответственно, будет меняться электропроводность. Значит, электропроводность зависит от температуры.

Впоследствии эти методы были развиты английским логиком-позитивистом ХIХ в. Дж. Ст. Миллем (1806- 1873) и до сих пор известны как индуктивные методы Бэкона-Милля.

Контрольные вопросы:

1.Что такое индукция?

2.Какие бывают виды индуктивных умозаключений?

3.Что такое индуктивные методы Бэкона-Милля?

4.Сколько этих методов и как они называются?

ЛЕКЦИЯ 7. ДОКАЗАТЕЛЬСТВО И ОПРОВЕРЖЕНИЕ

Определение доказательства и опровержения

Если умозаключение состоит из суждений, то доказательство состоит из умозаключений. И по существу мы с ним уже имели дело, когда рассматривали простой категорический силлогизм. Каноническая форма силлогизма строится так, что сначала идут посылки, а потом заключение. Но очень часто в обыденной речи и обыденном мышлении мы меняем посылки и заключение местами: мы говорим «негры не дышат жабрами, потому что ни один человек не дышит жабрами, а все негры — люди». И тогда умозаключение принимает

форму доказательства, или обоснования, как иногда выражаются, — по существу это одно и то же.

Особенность доказательства состоит также в том, что в доказательстве мы имеем дело с рядом следующих друг за другом умозаключений, в котором чисто формальные переходы перемежаются с содержательными, то есть вытекающими из содержания рассматриваемого предмета.

И, наконец, последнее. При рассмотрении формы умозаключения истинность и ложность посылок и заключения брались как условные: мы говорили, что при правильном заключении из истинных посылок должно получаться истинное заключение, и, наоборот, из ложных посылок должно получаться ложное заключение. В реальном доказательстве нас интересует именно истинность того положения, которое мы хотим доказать. Если же мы хотим доказать ложность данного положения, то это уже будет его опровержение.

Итак, доказательство — это способ установления истинности данного положения на основе других истинных положений.

Опровержение есть способ установления ложности данного положения на основе других истинных или ложных положений.

Структура доказательства

Во всяком доказательстве мы различаем три части: 1) доказываемое положение, или тезис, это то, что должно быть доказано; 2) основания доказательства, или аргументы, — это то, при помощи чего тезис доказывается; 3) форма доказательства, — это способ, каким тезис выводится из аргументов. Тезис в доказательстве соответствует заключению в силлогизме. Аргументы соответствуют посылкам силлогизма. Форома есть логическая схема (фигура или модус силлогизма), при помощи которой выводится заключение. Например, нужно доказать, что «железо плавко». Это есть тезис. Для доказательства можно воспользоваться следующими двумя аргументами: «все металлы плавки» и «железо есть металл». Из этого можно построить силлогизм, которым мы докажем тезис.

Прямое и косвенное доказательство

Прямым доказательством называется такое, когда прямо и непосредственно доказывается истинность данного тезиса. Но в действительности и в науке мы не всегда можем это сделать. И тогда прибегают к косвенному доказательству

, которое заключается в том, что мы доказываем не истинность тезиса, а ложность антитезиса. Антитезисом называется положение, противоречащее тезису. Истинность тезиса тогда следует по закону исключенного третьего А или не-А: если ложно не-А (антитезис), то истинно А (тезис).

В школьной математике косвенное доказательство называют обычно доказательством от противного. Например, требуется доказать, что в треугольнике, в котором два угла равны, противолежащие стороны тоже равны. Пусть в треугольнике АВС угол  равняется углу , и пусть противолежащие им стороны будут АС и ВС. Нам нужно доказать, что АС = ВС. Это есть тезис. Возьмем положение, противоречащее тезису: АСВС. Это будет антитезис. Существует теорема, согласно которой во всяком треугольнике против большего угла лежит большая сторона. И тогда из нашего антитезиса будет следовать, что угол  должен быть или больше, или меньше угла . Но это противоречит принятому нами положению. Отсюда следует, что антитезис ложен, и, следовательно, тезис истинен.

Последний шаг в этом доказательстве, как было сказано, основан на законе исключенного третьего: если ложен антитезис, то истинен тезис, а третьего не дано. А на чем же основан предыдущий шаг: из того, что принятый нами антитезис противоречит истинному положению, как следует ложность антитезиса? Это следует по закону противоречия: противоречащие друг другу положения не могут быть одновременно истинными и одновременно ложными, поэтому если одно из них истинно, то другое обязательно ложно. Поэтому такое доказательство в логике называется доказательством путем приведения к абсурду, reductio ad absurdum. Абсурдом в логике называется противоречие.

Правила и ошибки в доказательстве и опровержении

Доказательство и опровержение подчиняются правилам, которые вытекают из законов логики. Нарушение этих правил ведет к ошибкам. Преднамеренные ошибки называются софизмами, непреднамеренные — паралогизмами.

Правила и ошибки по отношению к тезису:

1. Тезис должен быть четко сформулирован и не содержать неопределенных терминов.

2. Тезис должен оставаться неизменным на протяжении всего доказательства, то есть нельзя подменять тезис.

Ошибки:

подмена тезиса — заключается в том, что обоснование или опровержение тезиса подменяется обоснованием совсем другого положения.
довод к личности — заключается в том, что обоснование или опровержение тезиса подменяется положительной или отрицательной оценкой личности человека, выдвинувшего тезис.
довод к публике — состоит в том, что вместо доказательства и опровержения стремятся повлиять на чувства людей, чтобы они поверили в истинность или ложность выдвинутого тезиса без его доказательства по существу.

Правила и ошибки по отношению к аргументам:

1.     Аргументы должны быть истинными, доказанными суждениями.

Ошибка: предвосхищение основания — в качестве аргументов используются положения, которые сами нуждаются в доказательстве.

2.     Истинность аргументов должна быть установлена независимо от тезиса.

Ошибка: круг в доказательстве («порочный круг») — тезис обосновывается аргументами, а аргументы тезисом.

3.     Аргументы не должны противоречить друг другу.

Ошибка: выдвижение аргументов, противоречащих друг другу.

4.     Аргументы должны быть необходимыми и достаточными для доказательства или опровержения тезиса.

Ошибки:

не хватает необходимых аргументов (слишком поспешное доказательство);
имеются лишние аргументы (чрезмерное доказательство).

Правила и ошибки по отношению к форме доказательства (к демонстрации):

Любое доказательство или опровержение должно строиться по законам и правилам логики. Нарушение любого правила и закона логики ведет к ошибке.