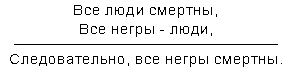ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 28.03.2024
Просмотров: 84
Скачиваний: 0
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
таблицами истинности. Для отрицания эта таблица будет очень простая
Для конъюнкции таблица будет такая:
Для дизъюнкции:
Для строгой дизъюнкции:
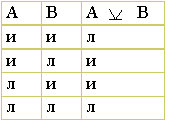
Для импликации:
Этот табличный способ задания логических функций позволяет построить так называемую логику высказываний, где из одной тождественноистинной формулы выводится другая тождественноистинная формула. Ведь если мы табличным способом установили тождественную истинность двух формул, например, формулы А и формулы Б, то мы их можем подставить на место переменных в импликативную функцию А → В, а это означает, что из А следует В.
Контрольные вопросы:
1.Что такое суждение?
2.Какова логическая форма суждения?
3.Какие существуют виды суждений?
4.Что означает распределенность терминов в суждении?
5.Что такое отношения между суждениями и какие могут быть отношения между суждениями?
6.Что такое «логический квадрат»?
7.Что такое законы логики?
8.Что такое основные законы логики?
9.Что такое необходимые и достаточные условия?
10.Как образуются сложные суждения?
11.Что такое таблицы истинности?
ЛЕКЦИЯ 3. УМОЗАКЛЮЧЕНИЕ КАК ФОРМА МЫШЛЕНИЯ
Умозаключением в логике называется такое умственное действие, когда из одного или более суждений получают другое новое суждение. Например, если снег скрипит, значит на улице мороз. Но это содержательное умозаключение, в данном случае на основании физической причинной связи. Формальная логика изучает другого рода умозаключения — умозаключения на основе логической формы суждений и формы их отношений. Например, как мы уже видели, из общего суждения следует частное. И это независимо от того, о чем конкретно идет речь: умозаключение делается на основании одной только формы суждения, «все S есть Р». И если содержанием этого суждения будет полнейшая нелепость, например, «все ёрики есть майорики», то из него все равно следует частное суждение «некоторые ёрики суть майорики». Правомерность содержательных умозаключений находится в компетенции конкретной науки или практики.
С формальным умозаключением мы, таким образом, уже имели дело. Но форм формального умозаключения значительно больше. Например, такого рода умозаключение:

Такое умозаключение в логике называется простым категорическим силлогизмом. Здесь на основании двух суждений, которые называются посылками, выводится третье, которое называется заключением. Здесь переход от первой посылки, «все люди дышат легкими», опосредован второй посылкой, «Иванов — человек». Но есть другой класс умозаключений, которые называются непосредственными. Их-то и необходимо рассмотреть в первую очередь.
Непосредственные умозаключения
Умозаключение, в котором заключение выводится из одной посылки, называется непосредственным. По существу такое умозаключение является формальным преобразованием исходного суждения или посылки. Но такое преобразование является в некоторых случаях полезным и даже необходимым для некоторых целей. Вопрос этот может проясниться при рассмотрении силлогистического умозаключения.
Непосредственное умозаключение осуществляется в трех формах, в формах превращения, обращения и противопоставления предикату.
Превращение
Превращением называется такое непосредственное умозаключение, когда в заключении субъектом является субъект исходного суждения, а предикатом — понятие, противоречащее предикату исходного суждения, причем связка меняется на противоположную. Одно отрицание, таким образом идет к предикату, другое — к связке. Общая схема превращения такова:
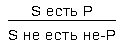
Эта общая схема превращения на кругах Эйлера будет выглядеть так:

Схемы превращения для разных видов суждений будут следующие:
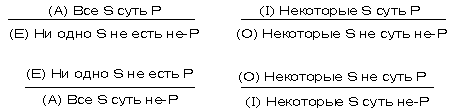
Смысл превращения заключается в выявлении того, что мыслимый предмет не может обладать свойством, противоречащим свойству, выражаемому предикатом. Здесь как бы уточняется значение исходного суждения.
Обращение
Обращением называется такое непосредственное умозаключение, в котором в выводе субъектом является предикат исходного суждения, а предикатом — субъект исходного суждения, при этом связка остается неизменной.
Но обращение, в отличие от превращения, не всегда сохраняет всеобщность исходного суждения. И тогда обращение оказывается с ограничением. Например, если мы имеем суждение «все люди дышат легкими», то мы не можем сказать, что «все дышащие легкими являются людьми», а мы можем сказать, что только «некоторые дышащие легкими суть люди». Это связано с тем, что предикат общеутвердительного суждения не распределен:
В некоторых случаях чистое, то есть с сохранением того же самого количества суждения, для общеутвердительных суждений возможно. Например, суждение «всякая молекула воды имеет формулу Н2О» обращается в суждение: «всякая молекула, имеющая формулу Н2О, есть молекула воды». Но это возможно только там, где суждение выражает сущность. Однако в общем виде в любом общеутвердительном суждении предикат не распределен, поэтому оно всегда обращается с ограничением.
Суждения вида (Е) обращаются в чистом виде, и это видно на кругах Эйлера:

Здесь всегда если никакое S не есть Р, то и никакое Р не есть S. Суждение вида (I) тоже всегда обращается в чистом виде. Но в некоторых случаях частноутвердительное суждение обращается в общеутвердительное суждение. Это возможно, если субъект исходного суждения является родовым по отношению к предикату. Например, суждение «некоторые дышащие легкими суть люди» обращается в суждение «все люди дышат легкими». Частноотрицательные суждения не обращаются. Например, если мы имеем суждение «некоторые люди не имеют высшего образования», то это можно интерпретировать двояко. На кругах Эйлера эти два случая выглядят следующим образом:
1)

2)

В первом случае из суждения «некоторые люди не имеют высшего образования» следует, что некоторые люди имеют высшее образование. Во втором случае этого не следует, потому что все остальные люди просто люди, и о них ничего определенного сказать нельзя.
Это понятно также, если учесть, что отрицание в логике имеет двоякое, по крайней мере, значение, соответствующее двум видам отношений между суждениями: противоположности и противоречия. Если мы имеем противоположность, например, между белым и черным, то отрицание белого вовсе не означает черный. Но если мы имеем противоречие, например, черный и нечерный, то отрицание одного необходимо влечет утверждение другого.
Обращение полезно, например, при проверке правильности определения понятия. Например, определение «треугольник есть плоская геометрическая фигура» может показаться правильным. Но стоит его обратить, как его неправильность станет очевидной: «плоская геометрическая фигура есть треугольник». Схемы обращения суждения суть следующие:
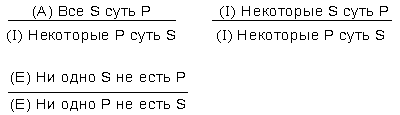
Противопоставление предикату
Противопоставлением предикату называется такое непосредственное умозаключение, когда в заключении субъектом является понятие, противоречащее предикату исходного суждения, а предикатом — субъект исходного суждения; при этом связка меняется на противоположную.
Противопоставление предикату соединяет в себе две предыдущие формы умозаключения: при противопоставлении предикату исходное суждение сначала нужно превратить, а потом обратить. Например, суждение «все млекопитающие — позвоночные животные», для того чтобы осуществить противопоставление предикату, сначала мы превращаем и получаем суждение «ни одно млекопитающее не является беспозвоночным животными, а затем полученное суждение обращаем и получаем «ни одно беспозвоночное животное не является млекопитающим».
Частноутвердительное суждение (I) нельзя противопоставить предикату, потому что путем превращения мы получаем из него суждение вида (О), а последнее, как мы видели обратить нельзя. Схемы противопоставления предикату суть следующие:

Контрольные вопросы:
2.Что такое непосредственное умозаключение?
3.Что такое превращение?
4.Что такое обращение?
5.Что такое противопоставление предикату?
ЛЕКЦИЯ 4. ДЕДУКТИВНЫЕ УМОЗАКЛЮЧЕНИЯ
Дедукция и индукция. Определение
Дедукцией (по-русски выведение) называется умозаключение от общего к частному. Примером может быть переход от общеутвердительного (А) суждения к суждению частноутвердительному (I). Это, так сказать, дедукция в чистом виде. И всякая формальная дедукция к этому, как это будет видно из дальнейшего, сводится.
Индукцией (по-русски наведение) называется умозаключение, наоборот, от частного к общему. Но такое умозаключение в чисто формальном плане может быть только вероятностным. Но об этом речь впереди.
Простой категорический силлогизм
Аксиома силлогизма
Всякое умозаключение всегда основано на каком-то необходимом и закономерном отношении. Если я по скрипу снега под ногами прохожих заключаю, что на улице мороз, то это заключение основано на том положении, что снег на морозе скрипит. Такие положения в математике называются аксиомами: это простейшие отношения и определения, на которых основаны все остальные положения математики. Попробуем присмотреться, на чем же основано силлогистическое умозаключение. Возьмем, например, такой случай:
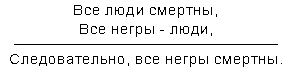
| А | A |
| И | Л |
| Л | И |
Для конъюнкции таблица будет такая:
| А | В | А В |
| и | и | и |
| и | л | л |
| л | и | л |
| л | л | л |
Для дизъюнкции:
| А | В | А В |
| и | и | и |
| и | л | и |
| л | и | и |
| л | л | л |
Для строгой дизъюнкции:

Для импликации:
| А | В | А В |
| и | и | и |
| и | л | л |
| л | и | и |
| л | л | и |
Этот табличный способ задания логических функций позволяет построить так называемую логику высказываний, где из одной тождественноистинной формулы выводится другая тождественноистинная формула. Ведь если мы табличным способом установили тождественную истинность двух формул, например, формулы А и формулы Б, то мы их можем подставить на место переменных в импликативную функцию А → В, а это означает, что из А следует В.
Контрольные вопросы:
1.Что такое суждение?
2.Какова логическая форма суждения?
3.Какие существуют виды суждений?
4.Что означает распределенность терминов в суждении?
5.Что такое отношения между суждениями и какие могут быть отношения между суждениями?
6.Что такое «логический квадрат»?
7.Что такое законы логики?
8.Что такое основные законы логики?
9.Что такое необходимые и достаточные условия?
10.Как образуются сложные суждения?
11.Что такое таблицы истинности?
ЛЕКЦИЯ 3. УМОЗАКЛЮЧЕНИЕ КАК ФОРМА МЫШЛЕНИЯ
Определение умозаключения
Умозаключением в логике называется такое умственное действие, когда из одного или более суждений получают другое новое суждение. Например, если снег скрипит, значит на улице мороз. Но это содержательное умозаключение, в данном случае на основании физической причинной связи. Формальная логика изучает другого рода умозаключения — умозаключения на основе логической формы суждений и формы их отношений. Например, как мы уже видели, из общего суждения следует частное. И это независимо от того, о чем конкретно идет речь: умозаключение делается на основании одной только формы суждения, «все S есть Р». И если содержанием этого суждения будет полнейшая нелепость, например, «все ёрики есть майорики», то из него все равно следует частное суждение «некоторые ёрики суть майорики». Правомерность содержательных умозаключений находится в компетенции конкретной науки или практики.
С формальным умозаключением мы, таким образом, уже имели дело. Но форм формального умозаключения значительно больше. Например, такого рода умозаключение:

Такое умозаключение в логике называется простым категорическим силлогизмом. Здесь на основании двух суждений, которые называются посылками, выводится третье, которое называется заключением. Здесь переход от первой посылки, «все люди дышат легкими», опосредован второй посылкой, «Иванов — человек». Но есть другой класс умозаключений, которые называются непосредственными. Их-то и необходимо рассмотреть в первую очередь.
Непосредственные умозаключения
Умозаключение, в котором заключение выводится из одной посылки, называется непосредственным. По существу такое умозаключение является формальным преобразованием исходного суждения или посылки. Но такое преобразование является в некоторых случаях полезным и даже необходимым для некоторых целей. Вопрос этот может проясниться при рассмотрении силлогистического умозаключения.
Непосредственное умозаключение осуществляется в трех формах, в формах превращения, обращения и противопоставления предикату.
Превращение
Превращением называется такое непосредственное умозаключение, когда в заключении субъектом является субъект исходного суждения, а предикатом — понятие, противоречащее предикату исходного суждения, причем связка меняется на противоположную. Одно отрицание, таким образом идет к предикату, другое — к связке. Общая схема превращения такова:
Эта общая схема превращения на кругах Эйлера будет выглядеть так:

Схемы превращения для разных видов суждений будут следующие:
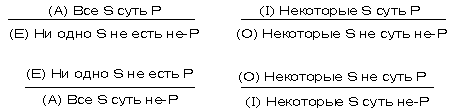
Смысл превращения заключается в выявлении того, что мыслимый предмет не может обладать свойством, противоречащим свойству, выражаемому предикатом. Здесь как бы уточняется значение исходного суждения.
Обращение
Обращением называется такое непосредственное умозаключение, в котором в выводе субъектом является предикат исходного суждения, а предикатом — субъект исходного суждения, при этом связка остается неизменной.
Но обращение, в отличие от превращения, не всегда сохраняет всеобщность исходного суждения. И тогда обращение оказывается с ограничением. Например, если мы имеем суждение «все люди дышат легкими», то мы не можем сказать, что «все дышащие легкими являются людьми», а мы можем сказать, что только «некоторые дышащие легкими суть люди». Это связано с тем, что предикат общеутвердительного суждения не распределен:
В некоторых случаях чистое, то есть с сохранением того же самого количества суждения, для общеутвердительных суждений возможно. Например, суждение «всякая молекула воды имеет формулу Н2О» обращается в суждение: «всякая молекула, имеющая формулу Н2О, есть молекула воды». Но это возможно только там, где суждение выражает сущность. Однако в общем виде в любом общеутвердительном суждении предикат не распределен, поэтому оно всегда обращается с ограничением.
Суждения вида (Е) обращаются в чистом виде, и это видно на кругах Эйлера:

Здесь всегда если никакое S не есть Р, то и никакое Р не есть S. Суждение вида (I) тоже всегда обращается в чистом виде. Но в некоторых случаях частноутвердительное суждение обращается в общеутвердительное суждение. Это возможно, если субъект исходного суждения является родовым по отношению к предикату. Например, суждение «некоторые дышащие легкими суть люди» обращается в суждение «все люди дышат легкими». Частноотрицательные суждения не обращаются. Например, если мы имеем суждение «некоторые люди не имеют высшего образования», то это можно интерпретировать двояко. На кругах Эйлера эти два случая выглядят следующим образом:
1)

2)

В первом случае из суждения «некоторые люди не имеют высшего образования» следует, что некоторые люди имеют высшее образование. Во втором случае этого не следует, потому что все остальные люди просто люди, и о них ничего определенного сказать нельзя.
Это понятно также, если учесть, что отрицание в логике имеет двоякое, по крайней мере, значение, соответствующее двум видам отношений между суждениями: противоположности и противоречия. Если мы имеем противоположность, например, между белым и черным, то отрицание белого вовсе не означает черный. Но если мы имеем противоречие, например, черный и нечерный, то отрицание одного необходимо влечет утверждение другого.
Обращение полезно, например, при проверке правильности определения понятия. Например, определение «треугольник есть плоская геометрическая фигура» может показаться правильным. Но стоит его обратить, как его неправильность станет очевидной: «плоская геометрическая фигура есть треугольник». Схемы обращения суждения суть следующие:

Противопоставление предикату
Противопоставлением предикату называется такое непосредственное умозаключение, когда в заключении субъектом является понятие, противоречащее предикату исходного суждения, а предикатом — субъект исходного суждения; при этом связка меняется на противоположную.
Противопоставление предикату соединяет в себе две предыдущие формы умозаключения: при противопоставлении предикату исходное суждение сначала нужно превратить, а потом обратить. Например, суждение «все млекопитающие — позвоночные животные», для того чтобы осуществить противопоставление предикату, сначала мы превращаем и получаем суждение «ни одно млекопитающее не является беспозвоночным животными, а затем полученное суждение обращаем и получаем «ни одно беспозвоночное животное не является млекопитающим».
Частноутвердительное суждение (I) нельзя противопоставить предикату, потому что путем превращения мы получаем из него суждение вида (О), а последнее, как мы видели обратить нельзя. Схемы противопоставления предикату суть следующие:

Контрольные вопросы:
2.Что такое непосредственное умозаключение?
3.Что такое превращение?
4.Что такое обращение?
5.Что такое противопоставление предикату?
ЛЕКЦИЯ 4. ДЕДУКТИВНЫЕ УМОЗАКЛЮЧЕНИЯ
Дедукция и индукция. Определение
Дедукцией (по-русски выведение) называется умозаключение от общего к частному. Примером может быть переход от общеутвердительного (А) суждения к суждению частноутвердительному (I). Это, так сказать, дедукция в чистом виде. И всякая формальная дедукция к этому, как это будет видно из дальнейшего, сводится.
Индукцией (по-русски наведение) называется умозаключение, наоборот, от частного к общему. Но такое умозаключение в чисто формальном плане может быть только вероятностным. Но об этом речь впереди.
Простой категорический силлогизм
Аксиома силлогизма
Всякое умозаключение всегда основано на каком-то необходимом и закономерном отношении. Если я по скрипу снега под ногами прохожих заключаю, что на улице мороз, то это заключение основано на том положении, что снег на морозе скрипит. Такие положения в математике называются аксиомами: это простейшие отношения и определения, на которых основаны все остальные положения математики. Попробуем присмотреться, на чем же основано силлогистическое умозаключение. Возьмем, например, такой случай: