Файл: Контрольные вопросы для самопроверки. Пособие содержит методические указания по теории погрешностей. Работы расположены в последовательности изложения материала курса Общая физика, раздел Механика.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 11.04.2024
Просмотров: 164
Скачиваний: 0
СОДЕРЖАНИЕ
ЧАСТЬ I. ЛАБОРАТОРНЫЕ РАБОТЫНАТУРНОГО ФИЗИЧЕСКОГО ЭКСПЕРИМЕНТА
Лабораторная работа № 1ОПРЕДЕЛЕНИЕ ЛИНЕЙНЫХ ВЕЛИЧИН И ПЛОТНОСТИ ТЕЛА
Лабораторная работа №2ПРОВЕРКА ОСНОВНОГО ЗАКОНА ДИНАМИКИПОСТУПАТЕЛЬНОГО ДВИЖЕНИЯ
Лабораторная работа №3ОПРЕДЕЛЕНИЕ КОЭФФИЦИЕНТА ТРЕНИЯ ПОКОЯ.
Лабораторная работа №4ОПРЕДЕЛЕНИЕ КОЭФФИЦИЕНТА ТРЕНИЯ СКОЛЬЖЕНИЯ
Лабораторная работа №5ОПРЕДЕЛЕНИЕ УСКОРЕНИЯ СВОБОДНОГО ПАДЕНИЯС ПОМОЩЬЮ МАШИНЫ АТВУДА
Лабораторная работа №6ИЗМЕРЕНИЕ СКОРОСТИ ПУЛИ С ПОМОЩЬЮБАЛЛИСТИЧЕСКОГО МАЯТНИКА
Лабораторная работа №7УПРУГОЕ СОУДАРЕНИЕ ШАРОВ
Лабораторная работа №8НЕУПРУГОЕ СОУДАРЕНИЕ ШАРОВ
Лабораторная работа №9ОПРЕДЕЛЕНИЕ МОМЕНТА ИНЕРЦИИ МАЯТНИКА ОБЕРБЕКА
Лабораторная работа №10ОПРЕДЕЛЕНИЕ МОМЕНТА ИНЕРЦИИ ТЕЛА ЭНЕРГЕТИЧЕСКИМ МЕТОДОМ
Лабораторная работа №11СКАТЫВАНИЕ ТВЕРДОГО ТЕЛА С НАКЛОННОЙ ПЛОСКОСТИ
Лабораторная работа №12МАТЕМАТИЧЕСКИЙ МАЯТНИК
Лабораторная работа №13ФИЗИЧЕСКИЙ МАЯТНИК
ЧАСТЬ II. ПОДСЧЕТ ПОГРЕШНОСТЕЙ ИЗМЕРЕНИЙ
Погрешность однократного прямого измерения
Учет случайной ошибки нескольких измеренийи ошибки однократного измерения
Алгоритм вычисления ошибки прямых равноточных измерений
Относительная погрешность — отношение абсолютной погрешности к истинному значению или к результату измерения. Относительная погрешность чаше всего выражается в процентах.
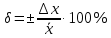
Приведенная погрешность
 где
где 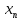 — нормированное значение величины.
— нормированное значение величины. В зависимости от характера проявления, причин возникновения и возможностей устранения различают систематическую и случайную составляющую погрешности измерения, а также грубые погрешности (промахи).
Систематические погрешности (ошибки) - это погрешности, которые сохраняют величину и знак от опыта к опыту, при равноточных измерениях. Типичными источниками систематических погрешностей бывают:
-
несовершенство используемой измерительной аппаратуры, -
несовершенство используемого метода измерений; -
плохая настройка измерительной аппаратуры; -
недостаточное постоянство условий опыта; -
влияние окружающей среды; -
постоянные ошибки экспериментатора; -
неучтенные влияния других параметров
Обнаружить и исключить систематические погрешности обычно нелегко. Можно изменить условия проведения опыта или проверить все перечисленные источники погрешности. В любом случае систематические погрешности можно избежать или уменьшить лишь при критическом отношении к методам исследования, совершенствуя их, применяя более точные приборы, следя за их исправностью и т. д.
Случайные погрешности (ошибки) — это погрешности, изменяющие свою величину или знак от опыта к опыту, при измерениях, выполненных одинаковым образом. Случайные погрешности обуславливаются большим числом случайных причин, действующих в каждом отдельном измерении различным, неизвестным образом. К числу таких причин относятся случайные вибрации отдельных частей прибора, различные изменения в среде (температурные, оптические, электрические, магнитные воздействия, изменение влажности, колебание воздуха), различное трение, физиологическое изменение органов чувств исполнителя (например, утомление) и множество других причин, которые практически невозможно учесть. Предсказать величину случайной погрешности для одного измерения в принципе невозможно. Поэтому приходится повторять измерения до определенного разумного предела, а полученную совокупность экспериментальных результатов обрабатывать с помощью теории вероятностей и математической статистики. Обе математические дисциплины образуют основу так называемой теории погрешностей.
С общей точки зрения ошибки обоих видов являются случайными величинами. Случайной величиной называется величина, принимающая в результате эксперимента числовое значение, которое принципиально нельзя предсказать, исходя из условий эксперимента.
Промахи или грубые погрешности (ошибки) - это ошибочные измерения или наблюдения, возникающие в результате небрежности при отсчете по прибору или неразборчивой записи показаний, при неправильном включении прибора, или при нарушении условий, в которых должен проводиться опыт (изменение напряжений, загрязнение материала и т. д.). При вычислении измеряемой величины такие ошибочные данные следует отбросить или сделать повторные (контрольные) измерения. В теории погрешностей измерений существует математический прием, позволяющий сделать точное заключение: является ли данное отклонение промахом и его следует отбросить или оно является закономерным отклонением измеряемой величины и должно быть включено в вычисление результата.
Познакомимся с некоторыми основными положениями и выводами теории случайных погрешностей.
Определение случайной ошибки
Если исходить из предположения, что все систематические ошибки учтены, то в качестве результата измерения можно рассматривать наиболее вероятное значение соответствующей случайной величины. Чтобы найти это наиболее вероятное значение или хотя бы оценить его точность нужно знать распределение случайной величины.
Анализ различных случайных величин, как изучаемых теоретически, так и вычисляемых на основании опытов, показывает существование одного наиболее часто встречающегося распределения, называемого нормальным или распределением Гаусса.
Распределение Гаусса получено на основе следующих двух допущений:
1) окончательная ошибка любого измерения представляет собой результат большого числа очень малых величин, распределенных случайным образом;
2) положительные и отрицательные отклонения относительно истинного значения равновероятны; иимеет вид рис. 1 (где f(x) плотность вероятности,
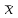 - наиболее вероятное значение).
- наиболее вероятное значение).
рис. 1
Кривая, изображенная нарис.1. непрерывна, т.е. описывает совокупность, содержащую бесконечное множество измерений, Это так называемая генеральная совокупность, из которой для исследования берутся некоторые конечные выборки.
Погрешность прямых, многократных, равноточных измерений
одной и той же физической величины
Рассмотрим выборку из n отсчетов, содержащую значения x1, x2, x3, …, xn полученные при повторных измерениях одной и той же величины. Допустим, что эти отсчеты составляют некоторую часть бесконечной нормально распределенной совокупности с неизвестным истинным значением.
Из свойства нормального распределения случайных величин следует, что наиболее вероятное значение
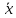 равно среднему арифметическому значению полученных
равно среднему арифметическому значению полученных
n отсчетов
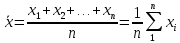 (1)
(1)Таким образом, в качестве результата измерений величины x нужно брать не числа x1, x2, x3, …, xn, а число
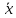 .
.Погрешность этого результата будет значительно меньше, но не следует думать, что
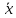 будет в точности равно истинному значению, так как
будет в точности равно истинному значению, так как 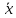 играет роль центра рассеяния.
играет роль центра рассеяния. Из эксперимента мы можем найти только отклонения отсчетов хi, от среднего
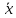 . Эти отклонения мы обозначим через Δxi:
. Эти отклонения мы обозначим через Δxi: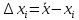 (2)
(2)Выборочной дисперсией
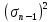 (или s2) измерения называют величину
(или s2) измерения называют величину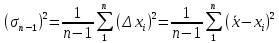 (3)
(3)Квадратный корень из выборочной дисперсии, т.е. величину
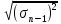 , называют среднеквадратичной погрешностью одного измерения:
, называют среднеквадратичной погрешностью одного измерения: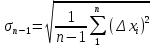
Среднеквадратичная погрешность характеризует степень разброса единичных измерений относительно x: в интервал
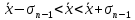 попадает примерно половина всех отсчетов хi.
попадает примерно половина всех отсчетов хi.Среднеквадратичное отклонение среднего значения
 можно вычислить по формуле
можно вычислить по формуле (5)
(5)Так как обычно число измерений n существенно меньше, чем требуется, то истинное значение x лежит в доверительном интервале
 , определяемом условием (6), с определенной доверительной вероятностью α.
, определяемом условием (6), с определенной доверительной вероятностью α. (6)
(6)где
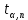 – коэффициент Стьюдента; n - объем выборки.
– коэффициент Стьюдента; n - объем выборки.Значение коэффициента Стьюдента берется из таблицы 1. При выполнении лабораторных работ доверительная вероятность обычно выбирается равной 0,95 (95%)
Условие (6) представляет собой абсолютную случайную ошибку измерений.
Тогда результат измерения величины xбудет находиться в интервале значений
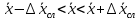 (7)
(7)Относительная погрешность измерений равна
 (8)
(8)Таблица 1. Коэффициенты Стьюдента (часть таблицы,
полный вариант см. приложение)
| | n | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 20 | ||
| α | | |||||||||||||
| 0.9 | 6.31 | 2.92 | 2.35 | 2.13 | 2.02 | 1.94 | 1.89 | 1.86 | 1.83 | 1.81 | 1.72 | | ||
| 0.95 | 12.7 | 4.3 | 3.18 | 2.78 | 2.57 | 2.45 | 2.36 | 2.31 | 2.26 | 2.23 | 2.09 | | ||
| 0.99 | 63.66 | 9.92 | 5.84 | 4.6 | 4.03 | 3.71 | 3.5 | 3.36 | 3.25 | 3.17 | 2.85 | | ||
| 0.999 | 636.6 | 31.6 | 12.94 | 8.61 | 6.86 | 5.96 | 5.41 | 5.04 | 4.78 | 4.59 | 3.85 | | ||

