Добавлен: 12.04.2024
Просмотров: 90
Скачиваний: 0
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
СОДЕРЖАНИЕ
3.1.2. Абсолютно неупругий удар
Удар материальной точки о неподвижную поверхность
Прямой удар материальной точки о неподвижную поверхность
Косой удар материальной точки о неподвижную поверхность
Теорема о движении центра масс системы материальных точек при ударе
Прямой центральный удар двух абсолютно твердых тел
Рассмотрим атт массы м, закрепленное в точке о подпятником, а в точке в – подшипником (рис. 4).
Учитывая, что в данном случае, а, из формулы [6]
Условия отсутствия ударных реактивных импульсов атт, вращающегося относительно неподвижной оси
Удар материальной точки о неподвижную поверхность
Прямой удар материальной точки о неподвижную поверхность
Прямым ударом МТ о неподвижную поверхность называют такой удар, при котором скорость МТ в начале удара направлена по нормали к поверхности в момент ее соприкосновения с МТ.
Рассмотрим прямой удар свободно падающей МТ массой m о неподвижную горизонтальную плоскость или о поверхность, нормаль к которой в точке удара вертикальна (рис. 1).
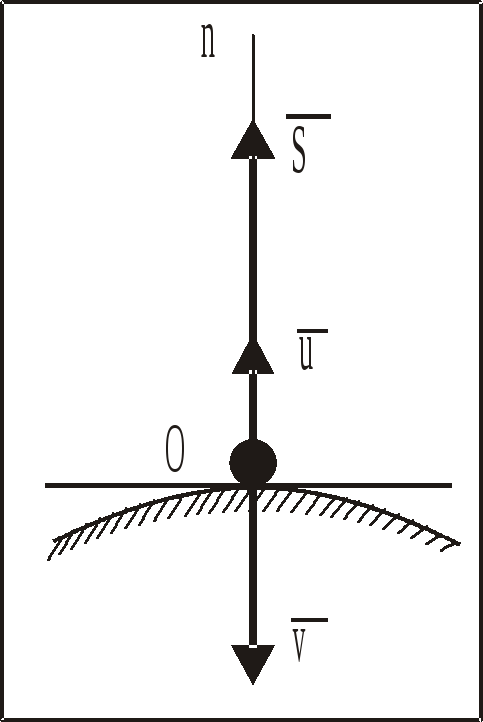 Рис. 1 [6]. | При таком ударе скорости МТ в начале и после удара направлены по нормали к поверхности в точке удара. Обозначим импульс этой ударной силы через Проектируя обе части этого равенства на внешнюю нормаль On в точке удара, получим [6]: |
При прямом ударе
Если скорость МТ в начале удара известна, то в уравнении (3) будут две неизвестные величины u и S. Очевидно, что для решения задачи необходимо получить дополнительную зависимость между входящими в уравнение (3) величинами.
Характер явления удара заставляет отступить от гипотезы абсолютно твердого тела и учитывать деформацию поверхности.
В ударе выделяют две фазы. В течение первой фазы поверхность деформируется (сжимается) до тех пор, пока скорость МТ не станет равной нулю
; при этом происходит переход кинетической энергии МТ во внутреннюю потенциальную энергию поверхности. В течение второй фазы удара форма поверхности под действием внутренних сил упругости частично восстанавливается. За эту вторую фазу скорость МТ возрастает до определенной конечной величины. Одновременно происходит переход внутренней потенциальной энергии поверхности в кинетическую энергию МТ. В тот момент, когда МТ отделится от поверхности, явление удара заканчивается. Во второй фазе удара восстанавливается только часть первоначальной кинетической энергии, а другая преобразуется в деформацию поверхности и ее нагревание.
Таким образом, скорость МТ в конце удара будет составлять какую-то часть скорости в начале удара и может быть определена равенством:
Отношение модулей скоростей шара после и до удара называется коэффициентом восстановления k при ударе.
Значение k для разных тел определяется опытным путем. Опыты показывают, что для различных тел k различно и изменяется от нуля до единицы (0 k 1).
Удар, при котором имеет место зависимость (4) при
Из уравнений (3) и (4), зная m, v , k, найдем неизвестные величины u, S:
u = kv.
Если k = 0, то такой удар называют абсолютно неупругим, и в этом случае явление удара заканчивается одной первой фазой. Так как в этом случае u=0, то при абсолютно неупругом ударе МТ, ударившись о неподвижную поверхность, остается неподвижной, при этом
Если же k = 1, то такой удар называют абсолютно упругим. В этом случае u = v, то есть скорость МТ в конце удара равна по модулю ее скорости в начале удара. При этом
Косой удар материальной точки о неподвижную поверхность
Косым ударом МТ с массой m об абсолютно гладкую неподвижную поверхность, называется такой удар, при котором скорость
Пусть угол – угол падения, а скорость в конце удара направлена к этой нормали под некоторым углом – угол отражения (рис. 2).
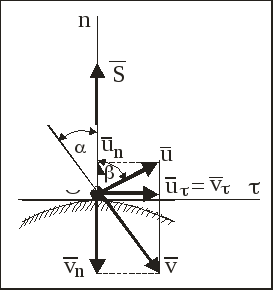 Рис. 2 [6]. | В рассматриваемом случае действующей на МТ ударной силой, как в случае прямого удара, будет нормальная реакция поверхности. Обозначим импульс этой ударной силы через Проектируя обе части уравнения (1) на нормаль к поверхности в точке удара и касательную, проведенную в плоскости векторов 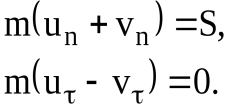 (5) (5) |
Из последнего равенства следует, что
то есть касательная составляющая скорости МТ при ударе об идеальную гладкую поверхность не изменяется.
Так как влиянием трения пренебрегаем и, следовательно, удар происходит только по направлению нормали к поверхности в точке удара, то аналогично соотношению (4), запишем:
В результате из соотношений (5) и (6) можно найти модуль и направление скорости МТ в конце удара и ударный импульс, если m, v и k известны [6]:
На рис. 2 видно, что
Поделив эти соотношения почленно и учтя, что
то есть в случае косого удара коэффициент восстановления есть отношение тангенса угла падения к тангенсу угла отражения. При не вполне упругом ударе
В частном случае абсолютно упругого удара
Теорема об изменении количества движения системы материальных точек при ударе
Рассмотрим систему материальных точек (далее – СМТ), состоящую из n МТ, и выделим -ю МТ с массой
Так же как при доказательстве общих теорем динамики СМТ, разделим все ударные импульсы, действующие на МТ, на внешние и внутренние. Тогда основное уравнение теории удара (1) для -й МТ рассматриваемой СМТ примет вид [6]:
где
и
Составив такие уравнения для всех n МТ рассматриваемой СМТ и сложив их почленно, получим [2, 3, 6]:
Введя следующие обозначения:
Теорема: Изменение количества движения СМТ за время удара равно геометрической сумме всех внешних ударных импульсов, действующих на эту СМТ.
Проектируя соотношение (8) на координатные оси, получим скалярную форму теоремы об изменении количества движения СМТ при ударе [6]:
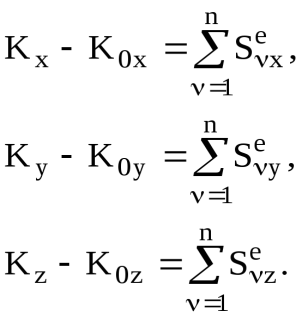 (9)
(9)Из соотношений (9) следует, что изменение проекции количества движения СМТ на какую-либо ось за время удара равно сумме проекций всех ударных импульсов внешних ударных сил, действующих на СМТ, на ту же ось.

