ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 27.04.2024
Просмотров: 39
Скачиваний: 0
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
После проведения N испытаний определяется приближённое значение искомой вероятности
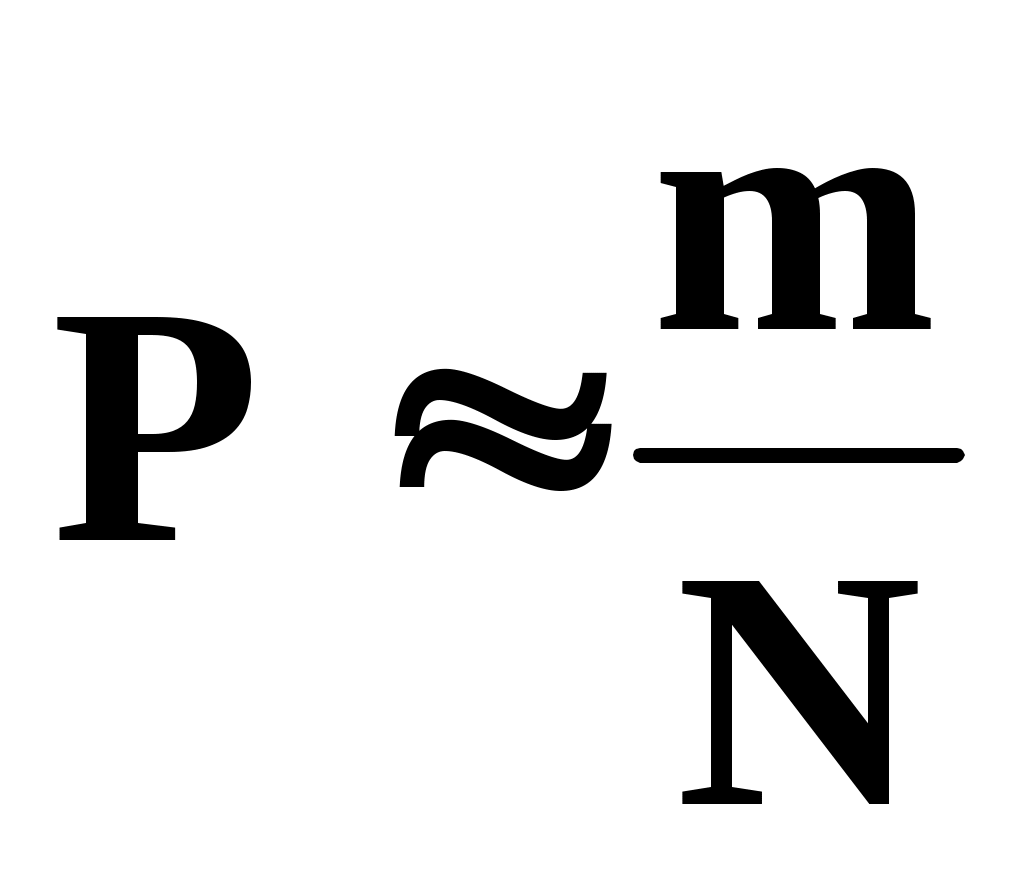 .
.
Описанная процедура не требует запоминания всех случайных чисел, извлекаемых в процессе счёта. По ходу вычисления запоминаются только число испытаний N и число удачных испытаний m.
Для того, чтобы метод статистических испытаний можно было считать практически приемлемым, необходимо оценить точность равенства (3) и на этом основании определить число испытаний N для вычисления интеграла (1) с достаточной точностью. Представление о точности можно получить, рассматривая , как случайную величину. Она имеет математическое ожидание
, как случайную величину. Она имеет математическое ожидание
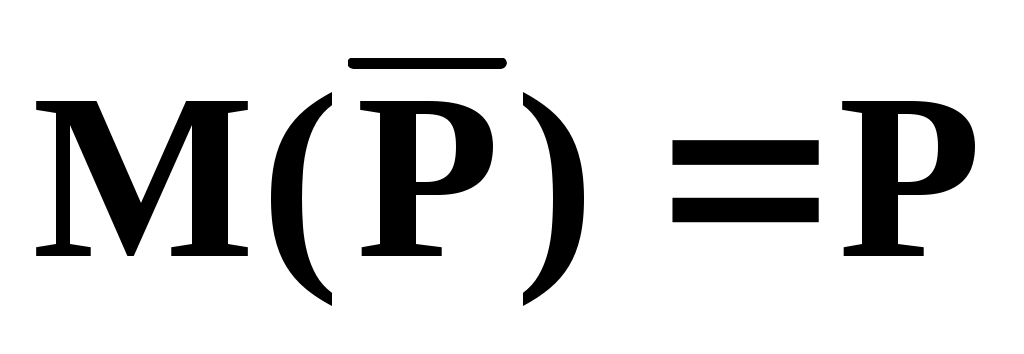
и дисперсию
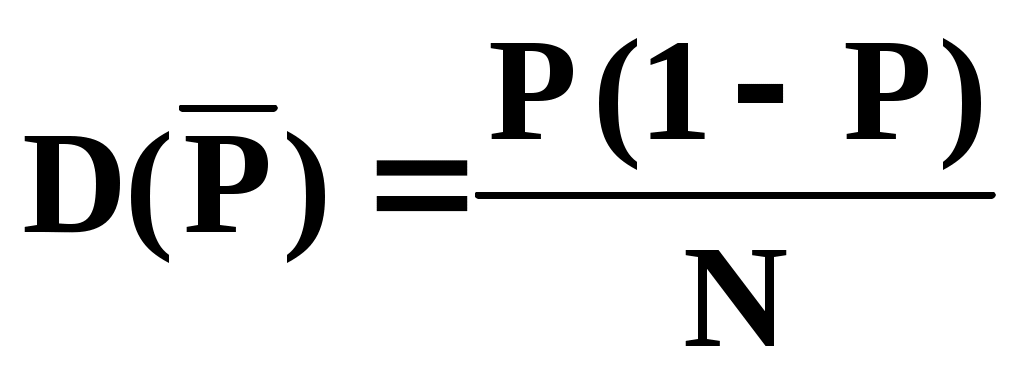 .
.
Поэтому средняя квадратичная ошибка равенства (3) будет равна
равенства (3) будет равна
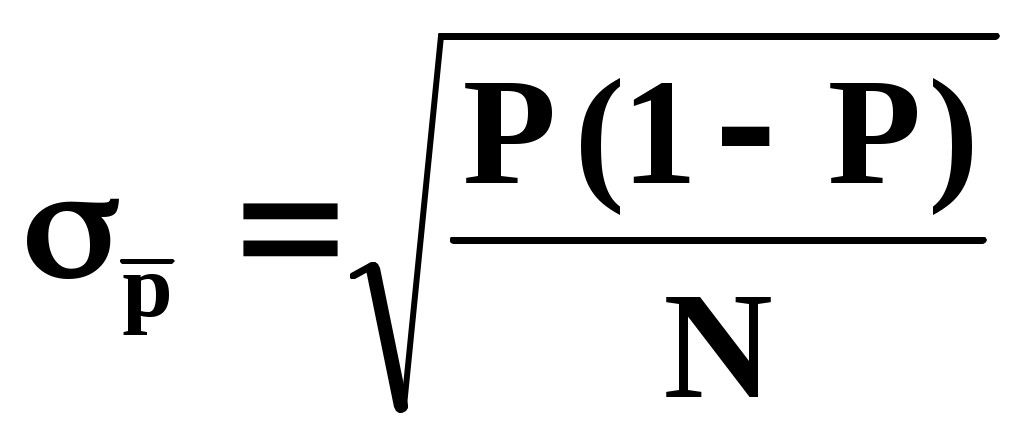 .
.
Легко видеть, что максимум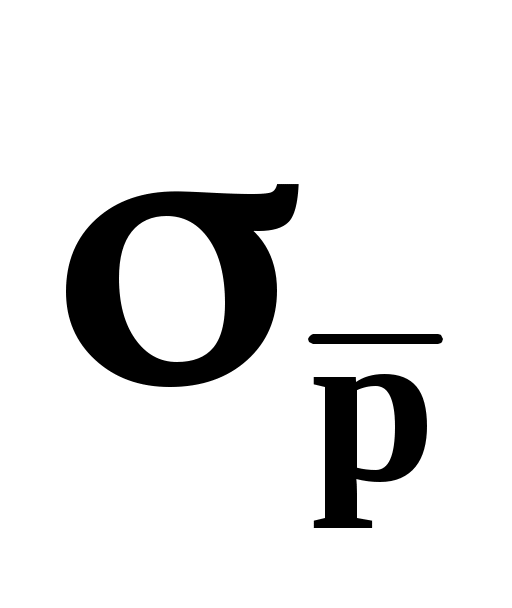 достигается при P = 0,5.
достигается при P = 0,5.
Обсудим вопрос о точности метода более подробно. Равенство (3) имеет точность с надежностью , если для неравенства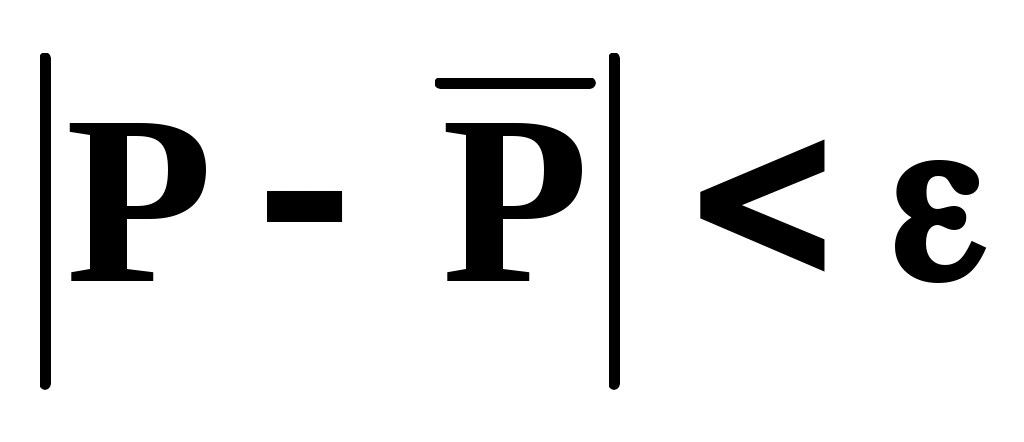 справедливо соотношение
справедливо соотношение
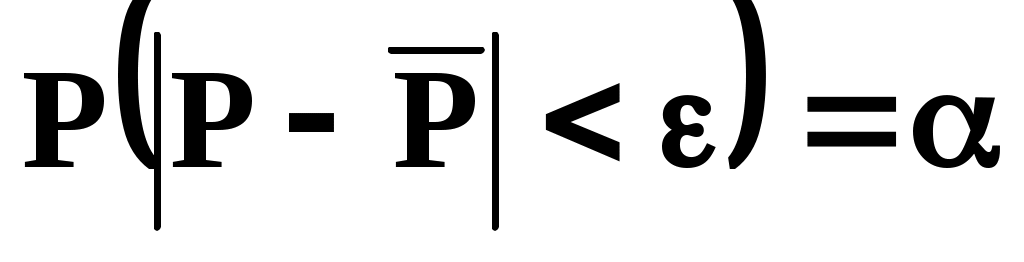 . (6)
. (6)
Смысл соотношения (6) можно пояснить на примере. Пусть =0,01; =0,95. Тогда при систематическом употреблении формулы (3) можно утверждать, что в среднем в 95 случаях на 100 испытаний приближенное значение искомой вероятности будет отличаться от её истинного значения p не более как на 0,01.
будет отличаться от её истинного значения p не более как на 0,01.
Свяжем величины и с числом испытаний N. Первую ориентировку в этом вопросе можно получить из неравенства Чебышева, справедливого для любой случайной величины. В наших обозначениях оно имеет вид
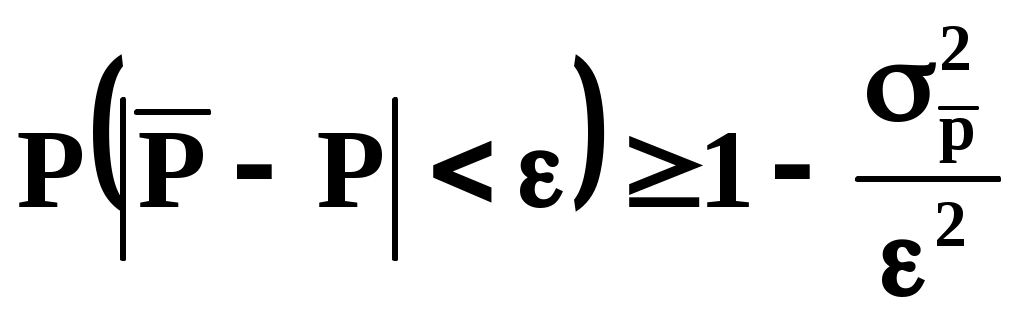
(54)
. (7)
Сопоставляя это выражение с (6), можно принять
 .
.
Если подставить теперь вместо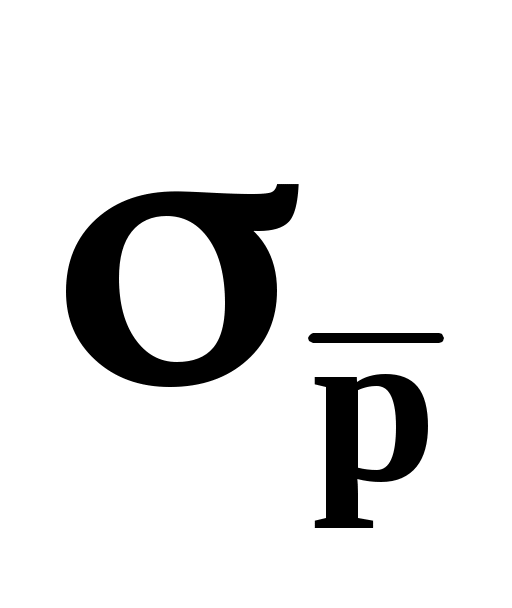 его значение из (5), получим
его значение из (5), получим
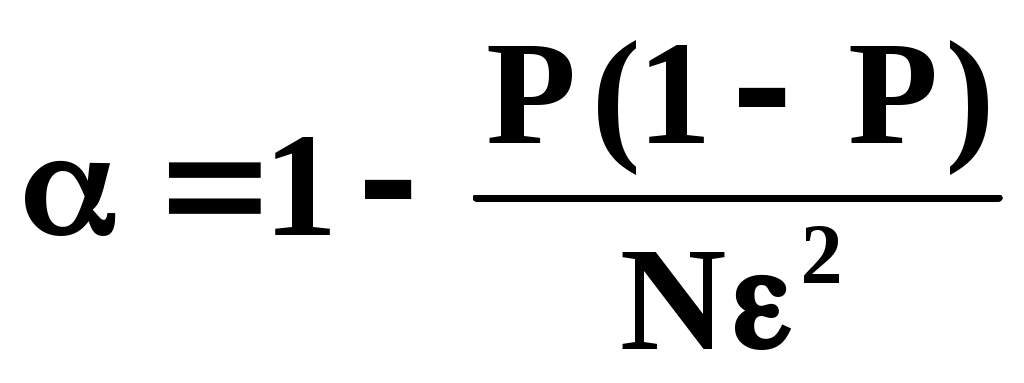 .
.
Отсюда
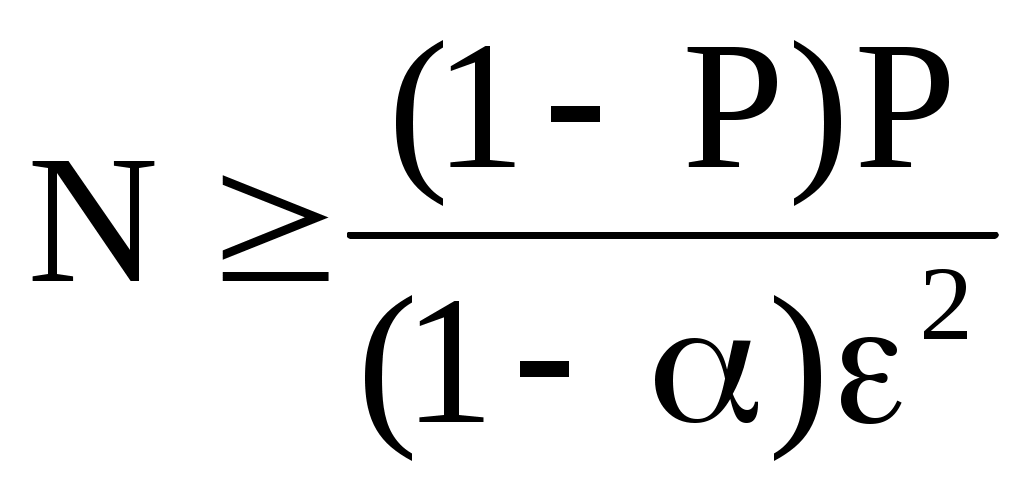 . (8)
. (8)
В соответствии с (8) можно вычислить число испытаний N, если заданы , и P. Например, если мы хотим, чтобы с надёжностью =0,95 погрешность не превышала 0,01 при P=0,5, необходимо выполнить не менее N=50 000 испытаний.
Формула (8), полученная на основании неравенства Чебышева, даёт сильно завышенное значение N. Более точную оценку для N можно получить в том случае, если использовать закон распределения случайной величины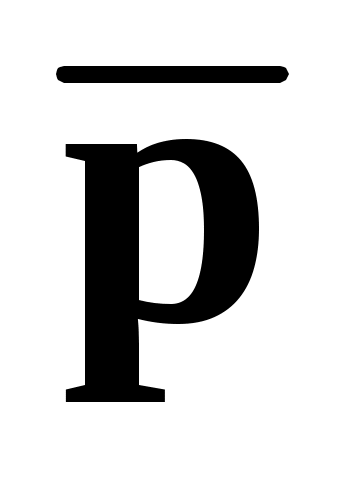 из равенства (6). Величина
из равенства (6). Величина  имеет (при N) асимптотически нормальное распределение. На этом основании при больших N равенство (6) можно записать в виде:
имеет (при N) асимптотически нормальное распределение. На этом основании при больших N равенство (6) можно записать в виде:
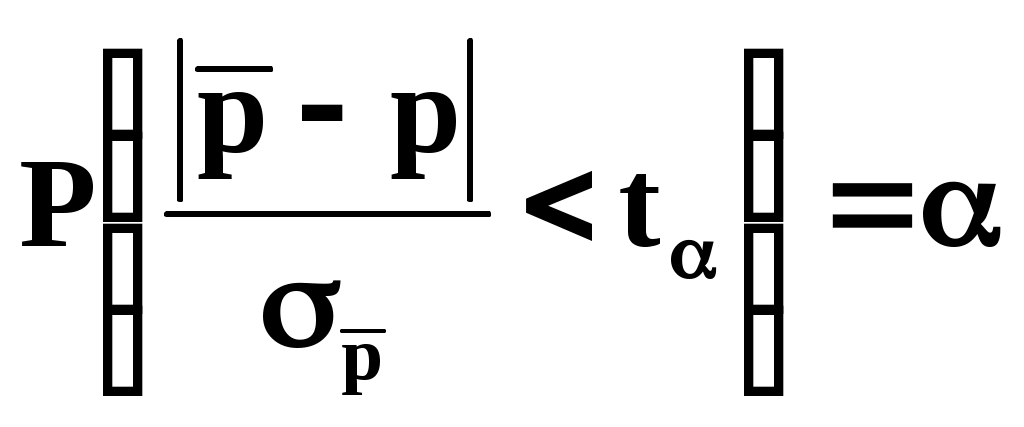 ,
,
где t – величина критического интервала, которая выбирается из таблиц нормального распределения по заданной надёжности . Сравнивая это соотношение с (6) мы видим, что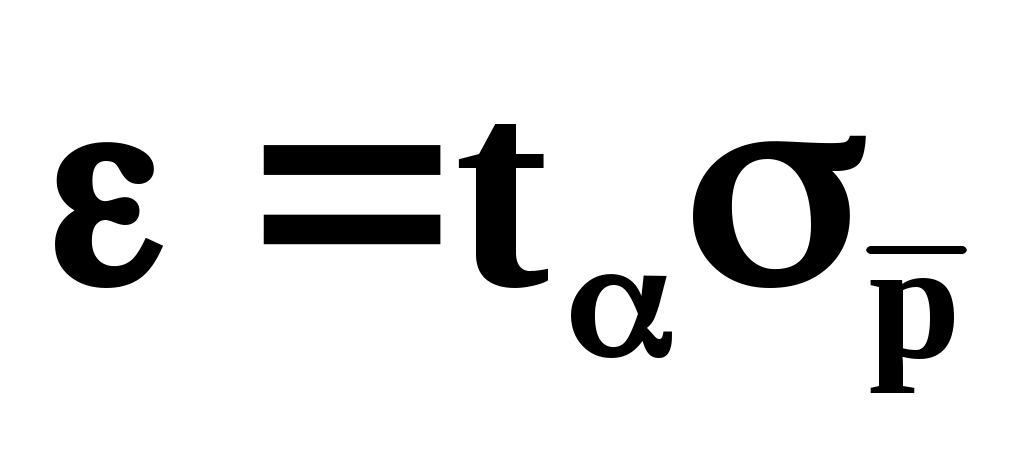 , или
, или
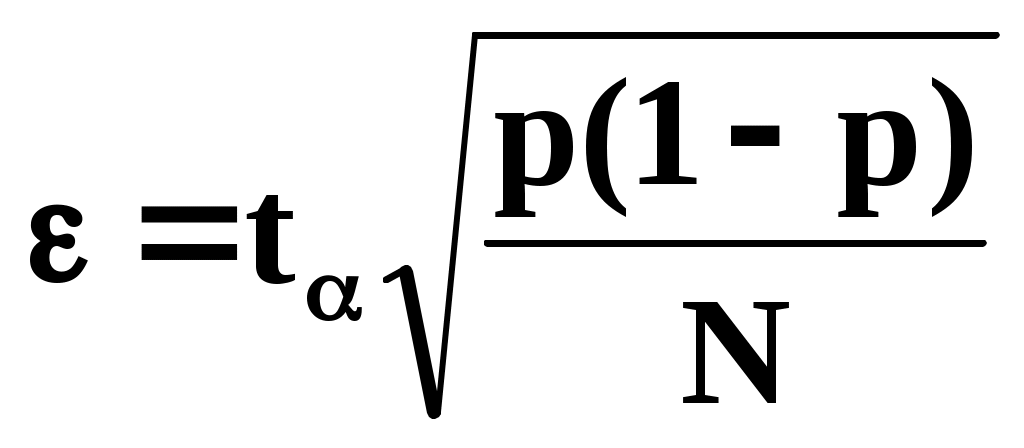 .
.
Отсюда можно определить значение N:
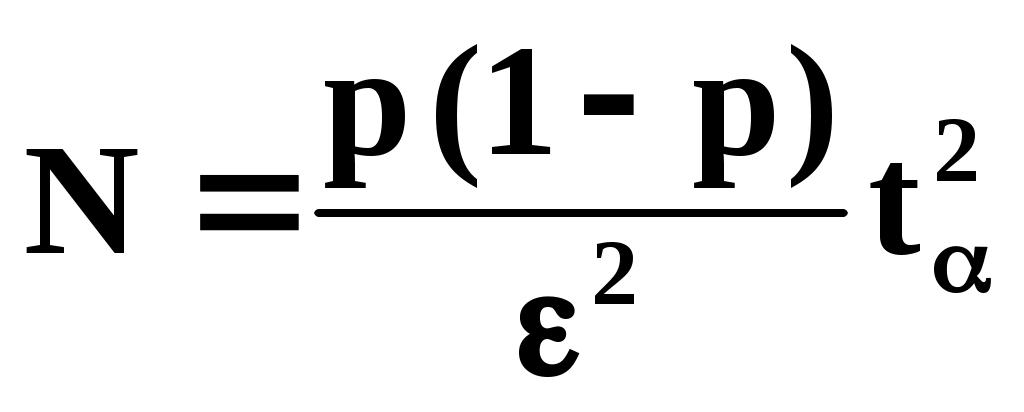 (9)
(9)
Для того, чтобы наглядно представить порядок величины N, обеспечивающей заданную точность, положим, как и прежде, =0,95 и вычислим N для различных значений p и . Результаты расчёта даны в таблице 1.
Из таблицы видно, что при увеличении точности (т.е. уменьшении ) существенно увеличивается необходимое число испытаний N. Это является одним из ограничений применимости данного метода. Его целесообразно применять для решения тех задач, где требования к точности не являются слишком жёсткими. На практике определение N затрудняется тем, что не всегда известно значение Р.
Допустимо в целях оценки N вместо Р брать частоту . Для этого выполняются следующие операции:
. Для этого выполняются следующие операции:
1) Сначала выбирается N=N0 (например для Р=0,1).
2) Затем, после N0 испытаний вычисляется и по формуле (9) уточняется значение N.
и по формуле (9) уточняется значение N.
3) Если NN0, то проводятся дополнительные испытания. В случае, когда после дополнительных испытаний происходит изменение , то уточнение значения N необходимо продолжить. Можно также пользоваться максимальным значением N при р=0,5.
, то уточнение значения N необходимо продолжить. Можно также пользоваться максимальным значением N при р=0,5.
Пусть требуется вычислить интеграл:
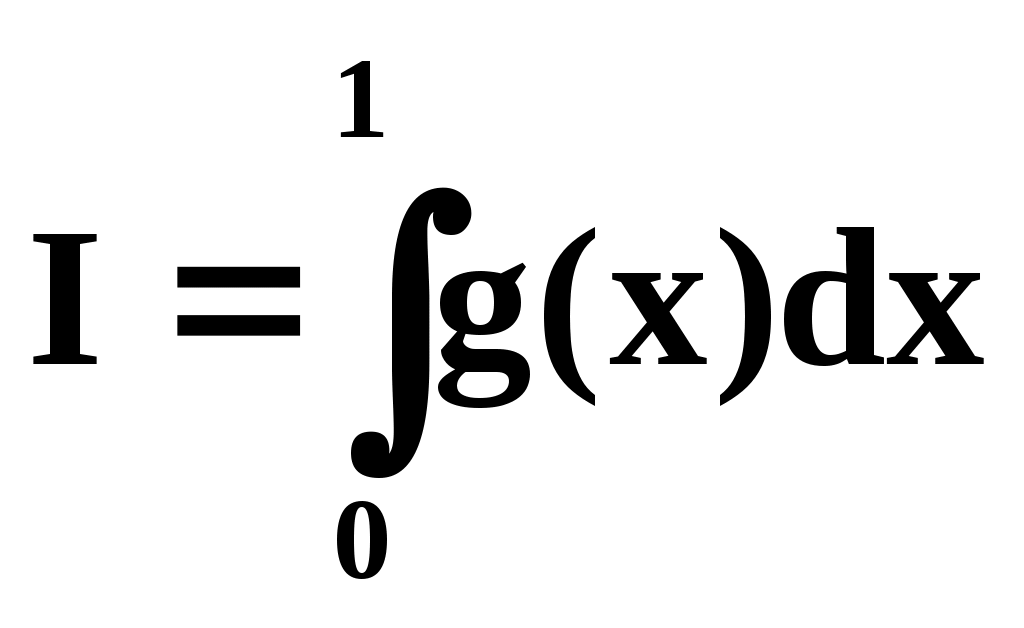 (10)
(10)
причём подынтегральная функция удовлетворяет условию
0g(x)1 (11)
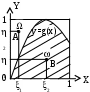
Будем рассматривать на плоскости две области:
1)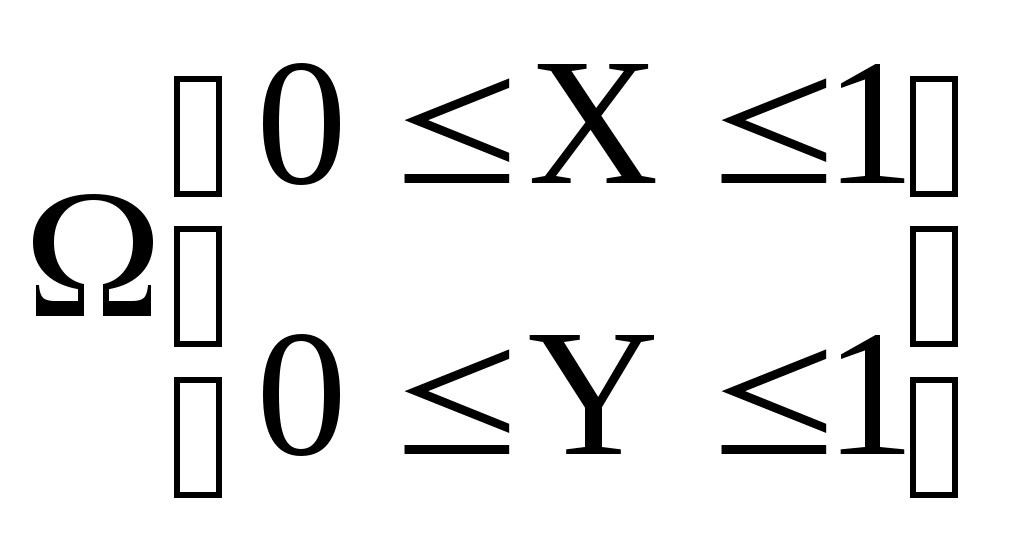
2) Область ограничена кривой y=g(x), осью ОХ и ординатами х=0; и х=1. Легко видеть, что величина интеграла I в точности равна площади S области , а площадь S=1. Зададим в области равномерное распределение случайной точки (,). Совместная функция плотности f(x,y) случайных величин и в области равна единице. Вероятность попадания точки (,) в область равна:
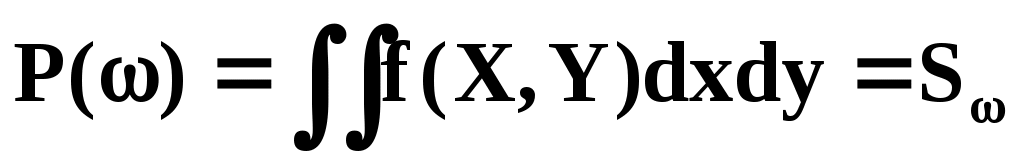
Проводим эксперимент по генерации значений координат точки (,): (Xi,Yi). Если появившаяся точка (Xi,Yi) принадлежит области , то испытание будем считать удачным. После проведения N испытаний подсчитаем число удачных испытаний и вычислим частоту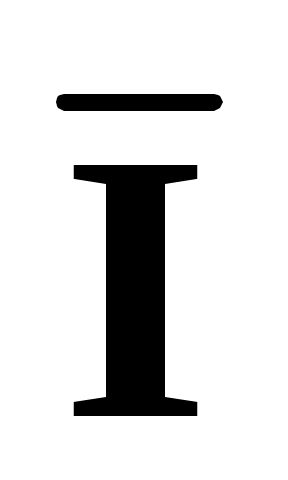 попадания случайной точки (,) в область :
попадания случайной точки (,) в область :

При N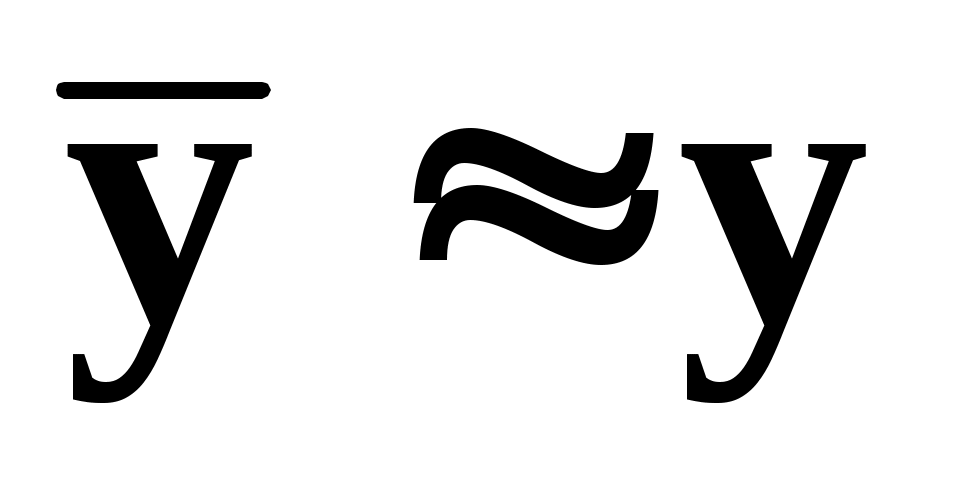 .
.
По данному алгоритму отметим два замечания:
yg(x) (13)
Предположим теперь, что необходимо вычислить интеграл:
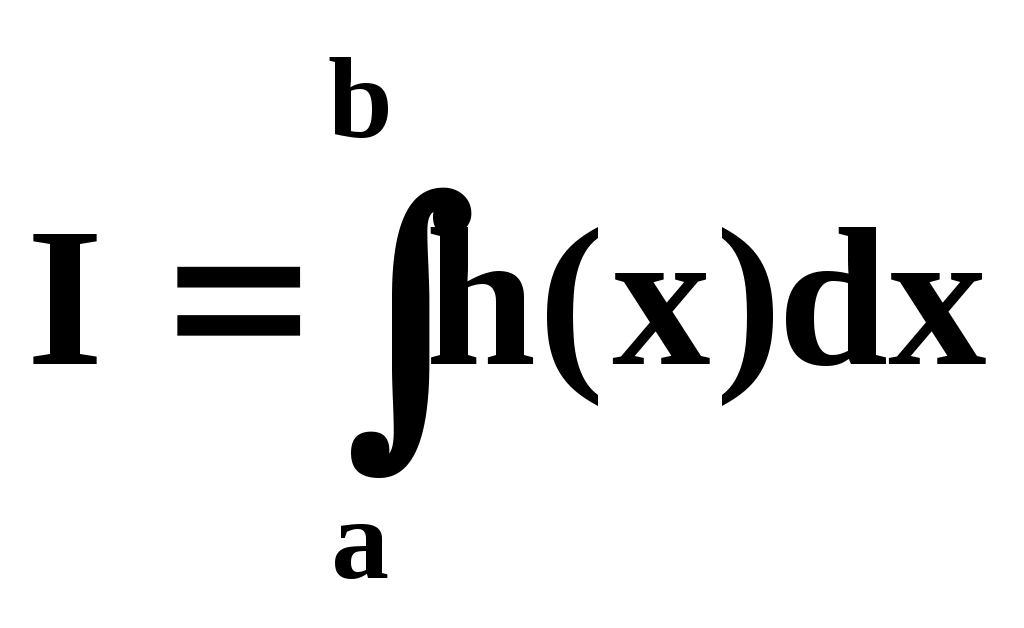 (14)
(14)
в конечных пределах (a,b). Обозначим наибольшее и наименьшее значения h(x) на (a,b) соответственно M и L. Заменой переменных X=a+(b
–a)Z и изменением масштаба по оси h(x) преобразуем интеграл (14) к виду:
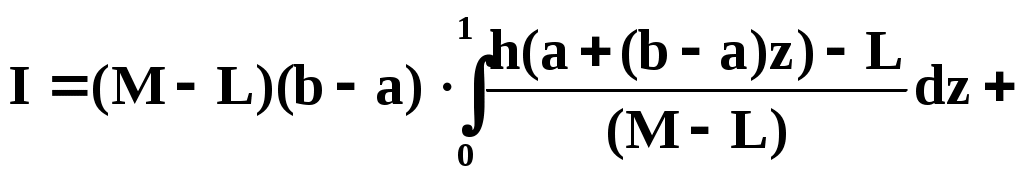
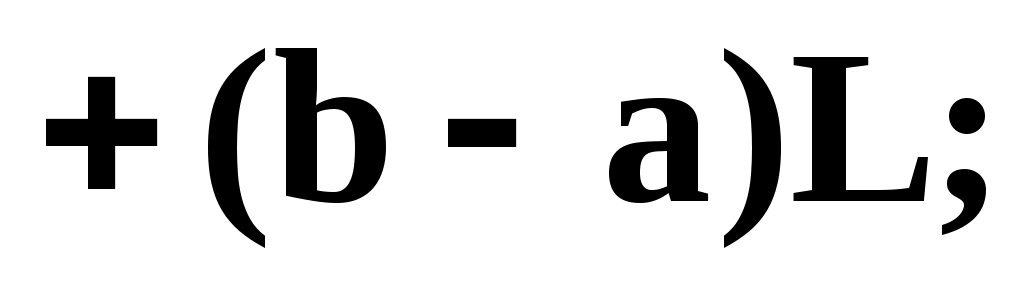
Введём обозначения:
(M–L)(b-a)=S
L(b–a)=S0
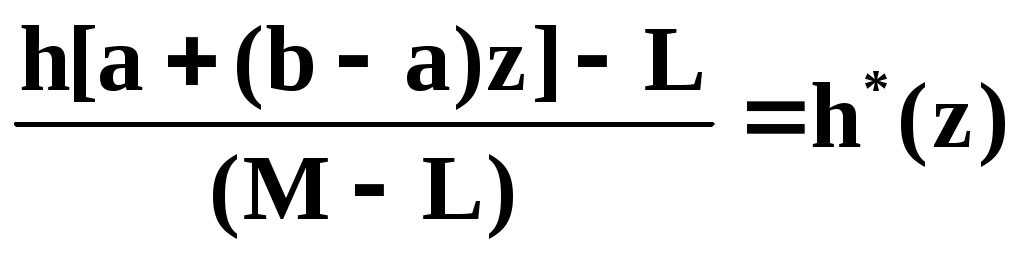
Тогда: I=SI*+S0, где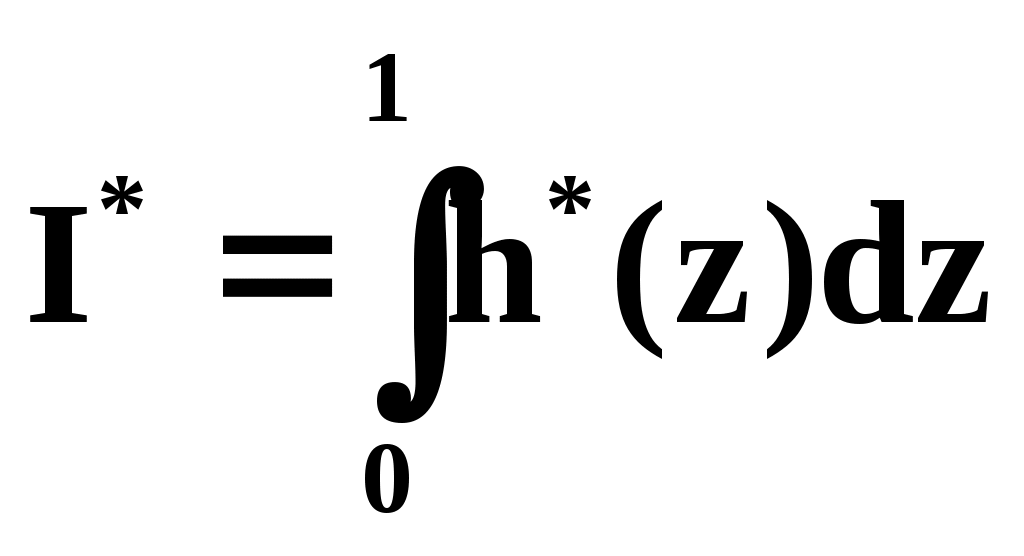
Таким образом, мы свели вычисление интеграла (14) к случаю (10) (где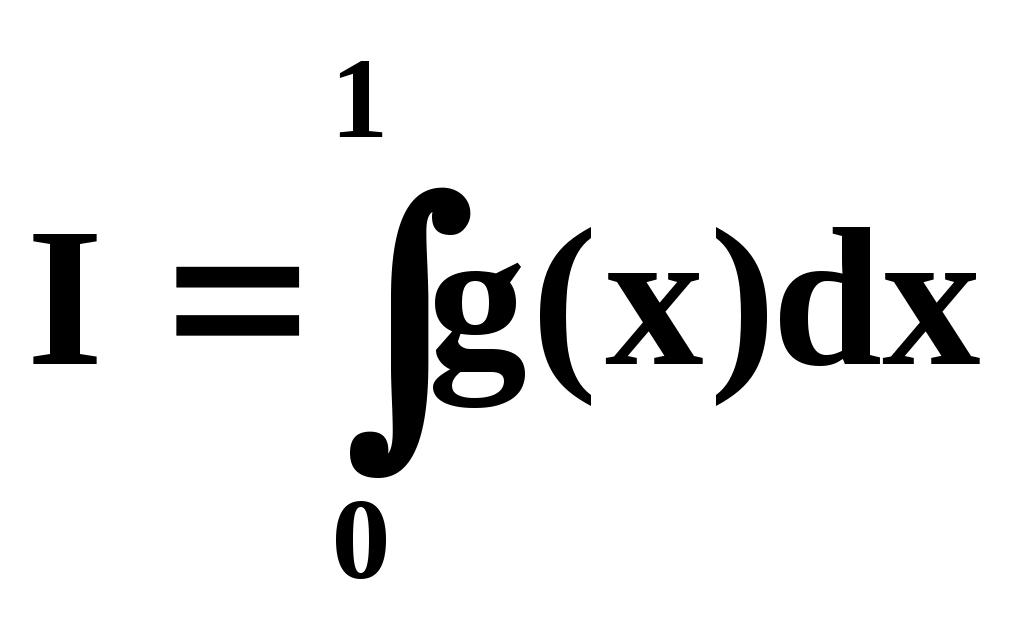 )
)
В разделе 4-й этап построения модели – проведение эксперимента мы отмечали следущее. «Экспериментальное исследование состоит в том, по крайней мере, из трёх разделов. 1.Измерение. 2.Аналитическое описание. 3.Феноменологическое описание результатов.». Рассмотрим первый раздел более подробно.
Классификация измерений
Измерения являются средством получения информации о свойствах физических объектов, о закономерностях протекающих процессов и т.д.
Измерение (согласно ГОСТ 16263-70) – это нахождение физической величины опытным путём с помощью специальных технических средств. Измерение – это операция, посредством которой определяется отношение измеряемой величины к другой однородной величине, принимаемой за единицу. Выражающая это отношение величина называется численным значением измеряемой величины.
Различают три наиболее общих метода измерений:
1. Прямые.
2. Косвенные.
3. Совокупные.
Эта классификация важна, т.к. каждая её категория связана с определённым способом обработки данных. Согласно ГОСТ 16263-70, совокупные измерения позже стали делить на собственно совокупные и совместные. При прямых измерениях объект исследования приводят во взаимодействие со средством измерений и по показаниям последнего отсчитывают значение измеряемой величины. Показания прибора могут умножаться на некоторый коэффициент, могут вводиться поправки и т.д. При косвенных измерениях искомое значение измеряемой величины находят на основании известной зависимости между этой величиной и величинами-аргументами. Аргументы находят прямыми или другими способами измерений. Например,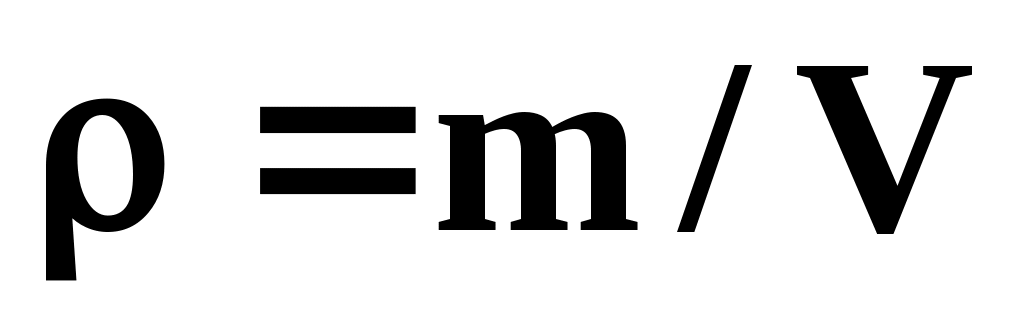
Описанная процедура не требует запоминания всех случайных чисел, извлекаемых в процессе счёта. По ходу вычисления запоминаются только число испытаний N и число удачных испытаний m.
Для того, чтобы метод статистических испытаний можно было считать практически приемлемым, необходимо оценить точность равенства (3) и на этом основании определить число испытаний N для вычисления интеграла (1) с достаточной точностью. Представление о точности можно получить, рассматривая
и дисперсию
Поэтому средняя квадратичная ошибка
Легко видеть, что максимум
Обсудим вопрос о точности метода более подробно. Равенство (3) имеет точность с надежностью , если для неравенства
Смысл соотношения (6) можно пояснить на примере. Пусть =0,01; =0,95. Тогда при систематическом употреблении формулы (3) можно утверждать, что в среднем в 95 случаях на 100 испытаний приближенное значение искомой вероятности
Свяжем величины и с числом испытаний N. Первую ориентировку в этом вопросе можно получить из неравенства Чебышева, справедливого для любой случайной величины. В наших обозначениях оно имеет вид
(54)
. (7)
Сопоставляя это выражение с (6), можно принять
Если подставить теперь вместо
Отсюда
В соответствии с (8) можно вычислить число испытаний N, если заданы , и P. Например, если мы хотим, чтобы с надёжностью =0,95 погрешность не превышала 0,01 при P=0,5, необходимо выполнить не менее N=50 000 испытаний.
Формула (8), полученная на основании неравенства Чебышева, даёт сильно завышенное значение N. Более точную оценку для N можно получить в том случае, если использовать закон распределения случайной величины
где t – величина критического интервала, которая выбирается из таблиц нормального распределения по заданной надёжности . Сравнивая это соотношение с (6) мы видим, что
Отсюда можно определить значение N:
Для того, чтобы наглядно представить порядок величины N, обеспечивающей заданную точность, положим, как и прежде, =0,95 и вычислим N для различных значений p и . Результаты расчёта даны в таблице 1.
Значения N при =0,95 и различных p и
| p | | ||||
| 0.05 | 0.01 | 0.005 | 0.001 | ||
| 0.1 | 0.9 | 140 | 3600 | 14000 | 360000 |
| 0.2 | 0.8 | 250 | 6200 | 25000 | 620000 |
| 0.3 | 0.7 | 330 | 8400 | 33000 | 840000 |
| 0.4 | 0.6 | 380 | 9400 | 38000 | 940000 |
| 0.5 | 390 | 9800 | 39000 | 980000 | |
Из таблицы видно, что при увеличении точности (т.е. уменьшении ) существенно увеличивается необходимое число испытаний N. Это является одним из ограничений применимости данного метода. Его целесообразно применять для решения тех задач, где требования к точности не являются слишком жёсткими. На практике определение N затрудняется тем, что не всегда известно значение Р.
Допустимо в целях оценки N вместо Р брать частоту
1) Сначала выбирается N=N0 (например для Р=0,1).
2) Затем, после N0 испытаний вычисляется
3) Если NN0, то проводятся дополнительные испытания. В случае, когда после дополнительных испытаний происходит изменение
Пусть требуется вычислить интеграл:
причём подынтегральная функция удовлетворяет условию
0g(x)1 (11)

Будем рассматривать на плоскости две области:
1)
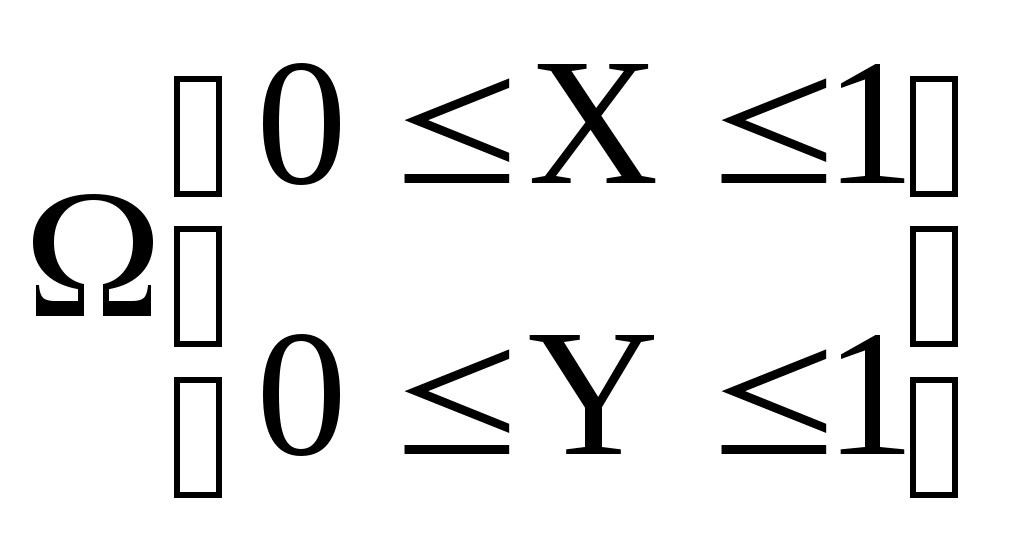
2) Область ограничена кривой y=g(x), осью ОХ и ординатами х=0; и х=1. Легко видеть, что величина интеграла I в точности равна площади S области , а площадь S=1. Зададим в области равномерное распределение случайной точки (,). Совместная функция плотности f(x,y) случайных величин и в области равна единице. Вероятность попадания точки (,) в область равна:
Проводим эксперимент по генерации значений координат точки (,): (Xi,Yi). Если появившаяся точка (Xi,Yi) принадлежит области , то испытание будем считать удачным. После проведения N испытаний подсчитаем число удачных испытаний и вычислим частоту
При N
По данному алгоритму отметим два замечания:
-
по получению координат Xi,Yi. Обычно имеется одномерная совокупность случайных чисел с равномерным распределением (0,1). Будем выбирать из этой совокупности пары последовательных чисел и будем считать их координатами Xi,Yi случайной точки. Точки с такими координатами будут иметь равномерное распределение в области ; -
по способу проверки факта попадания случайной точки в область . Для этого используется неравенство:
yg(x) (13)
Предположим теперь, что необходимо вычислить интеграл:
в конечных пределах (a,b). Обозначим наибольшее и наименьшее значения h(x) на (a,b) соответственно M и L. Заменой переменных X=a+(b
–a)Z и изменением масштаба по оси h(x) преобразуем интеграл (14) к виду:
Введём обозначения:
(M–L)(b-a)=S
L(b–a)=S0
Тогда: I=SI*+S0, где
Таким образом, мы свели вычисление интеграла (14) к случаю (10) (где
В разделе 4-й этап построения модели – проведение эксперимента мы отмечали следущее. «Экспериментальное исследование состоит в том, по крайней мере, из трёх разделов. 1.Измерение. 2.Аналитическое описание. 3.Феноменологическое описание результатов.». Рассмотрим первый раздел более подробно.
Классификация измерений
Измерения являются средством получения информации о свойствах физических объектов, о закономерностях протекающих процессов и т.д.
Измерение (согласно ГОСТ 16263-70) – это нахождение физической величины опытным путём с помощью специальных технических средств. Измерение – это операция, посредством которой определяется отношение измеряемой величины к другой однородной величине, принимаемой за единицу. Выражающая это отношение величина называется численным значением измеряемой величины.
Различают три наиболее общих метода измерений:
1. Прямые.
2. Косвенные.
3. Совокупные.
Эта классификация важна, т.к. каждая её категория связана с определённым способом обработки данных. Согласно ГОСТ 16263-70, совокупные измерения позже стали делить на собственно совокупные и совместные. При прямых измерениях объект исследования приводят во взаимодействие со средством измерений и по показаниям последнего отсчитывают значение измеряемой величины. Показания прибора могут умножаться на некоторый коэффициент, могут вводиться поправки и т.д. При косвенных измерениях искомое значение измеряемой величины находят на основании известной зависимости между этой величиной и величинами-аргументами. Аргументы находят прямыми или другими способами измерений. Например,


