ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 27.04.2024
Просмотров: 35
Скачиваний: 0
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
интерполяции и приближения функций, решения систем различных типов алгебраических и дифференциальных уравнений, исследование устойчивости и т.д.
Развитие вычислительной техники приводит к созданию программных комплексов, при использовании которых отпадает необходимость в программировании метода решения, т.е. достаточно лишь ограничиться заданием исходной информации. Это существенно снижает требования к знакомству пользователя ЭВМ с численными методами, но не устраняет полностью необходимости знакомства с вычислительным процессом.
Программные комплексы
мат. расчётов и моделирования
К числу современных пакетов прикладных программ (ППП), использующихся при мат. расчётах и моделировании, относятся: Scientific Work Place, Derive, MathCAD, Matematica, MatLAB и др. Все ППП имеют общий и хорошо известный из опыта работы с текстовыми и графическими редакторами набор файловых операций, вставки и удаления фрагментов, настройки системы, обеспечение справочной информацией. В них предусмотрены арифметические и логические операции, вычисление алгебраических и тригонометрических функций, решение систем алгебраических и дифференциальных уравнений и т.д. Новое поколение интегрированных ППП освоило и символьную форму представления уравнений, которая позволяет осуществлять перестановки, проводить операции с полиномами, разлагать функции Тейлора, решать дифференциальные уравнения и т.д.
Перечисленные возможности реализуются и в численной форме, а также используются в комбинации, когда сложное выражение преобразуется аналитически. В состав ППП входят также графические средства представления расчётов. Использование графических средств очень полезно, т.к. наш глаз способен выделять структуры и тренды, незаметные из табличных данных, а также обнаруживать изменения во времени, которые могут привести к пониманию важных механизмов, лежащих в основе поведения объекта. Они могут вычерчиваться как на плоскости, так и в пространстве в различных системах координат (т.е. в декартовой, в полярной, в цилиндрической и в сферической).
Метод статистических испытаний (метод Монте-Карло)
Одной из разновидностей мат. моделирования как чистого эксперимента является моделирование стохастических процессов. Это метод статистических испытаний или метод Монте-Карло, названный по аналогии с игрой в рулетку во всемирно известном казино Монте-Карло в Монако. Метод основан на многократном моделировании процесса при случайных воздействиях со статистической обработкой результатов испытаний (т.е. моделирования).
Хотя наибольшую пользу выборочный метод Монте-Карло приносит при моделировании вероятностных ситуаций, он приложим также и к некоторым полностью детерминистским задачам, не имеющим аналитического решения .
В методе Монте-Карло данные предшествующего опыта вырабатываются искусственно путем использования некоторого генератора случайных чисел в сочетании с интегральной функцией распределения вероятностей для исследуемого процесса. Таким генератором может быть таблица, колесо рулетки, подпрограмма ЭВМ или какой-либо другой источник равномерно распределенных случайных чисел.
Подлежащее разыгрыванию распределение вероятностей может быть основано на эмпирических данных, извлекаемых из ранее сформированных записей, или на результатах последнего эксперимента, либо может представлять собой известное теоретическое распределение. Случайные числа используются для получения дискретного ряда случайных переменных, имитирующего результаты, которых можно было бы ожидать в соответствии с разыгрываемым вероятностным распределением.
Способ применения метода Монте-Карло по идее довольно прост. Чтобы получить искусственную случайную выборку из совокупности величин, описываемой некоторой функцией распределения вероятностей, следует:
1. Построить график или таблицу интегральной функции распределения на основе ряда чисел, отражающего исследуемый процесс (а не на основе ряда случайных чисел), причем значения случайной переменной процесса откладываются по оси абсцисс (х), а значения вероятности (от 0 до 1)—по оси ординат (y).
2. С помощью генератора случайных чисел выбрать случайное десятичное число (СЧ) в пределах от 0 до 1 (с требуемым числом разрядов).
3. Провести горизонтальную прямую от точки на оси ординат, соответствующей выбранному СЧ, до пересечения с кривой распределения вероятностей.
4. Опустить из этой точки пересечения перпендикуляр на ось абсцисс.
5. Записать полученное значение х. Далее оно принимается как выборочное значение.
6. Повторить шаги 2—5 для всех требуемых случайных переменных, следуя тому порядку, в котором они были записаны.
Метод статистического моделирования Монте-Карло применяется для исследования и анализа характеристик радиокомпонентов при значительных отклонениях параметров от их средних значений (например, в программах Pspice, Electronics Workbench, и др.). Следует отметить, что в случае больших отклонений
хi входных параметров применение приближенных расчетных формул, полученных при использовании вероятностно-статистического метода анализа точности, приводит к значительным погрешностям полученных результатов.
Применение метода Монте-Карло позволяет получить функцию распределения плотности вероятности параметров радиокомпонентов. По графику этой функции можно определить не только среднее значение выходного параметра, но и предельные отклонения параметра, а также вероятность попадания параметра в заданные границы поля допуска.
При использовании метода статистического моделирования исследованию может подвергаться любая аналитически заданная функция вида
y = f(x1, x2,…xn) .
Объем вычислений при этом существенно увеличивается и для расчетов используется ЭВМ.
В качестве примера исследуем методом Монте-Карло функцию, выражающую зависимость выходного параметра радиокомпонента у от комплексного воздействия дестабилизирующих факторов (температуры, времени, влажности):
где yн – номинальное значение параметра; y,T – температурный коэффициент; y,t – коэффициент старения; - коэффициент влажности.
Значениями дестабилизирующих факторов являются: T – изменение температуры; t – промежуток времени, для которого рассчитывается изменение параметра у; значение влажности окружающей среды, косвенно задаваемое через величину коэффициента влажности .
Значения дестабилизирующих факторов (T, t, и влажности) являются детерминированными, т.е. неслучайными величинами.
Сущность метода Монте-Карло для анализа отклонения параметров радиокомпонентов может быть выражена в виде следующего алгоритма:
1. Рассчитывается или задается объем выборки радиокомпонентов N, необходимый для обеспечения достаточной точности проведения расчетов.
2. Измеряется N значений исследуемого параметра yn радиокомпонента, а также определяется N значений входных параметров (в данном случае коэффициентов нестабильности).
3. В расчетную формулу случайным образом подставляются значения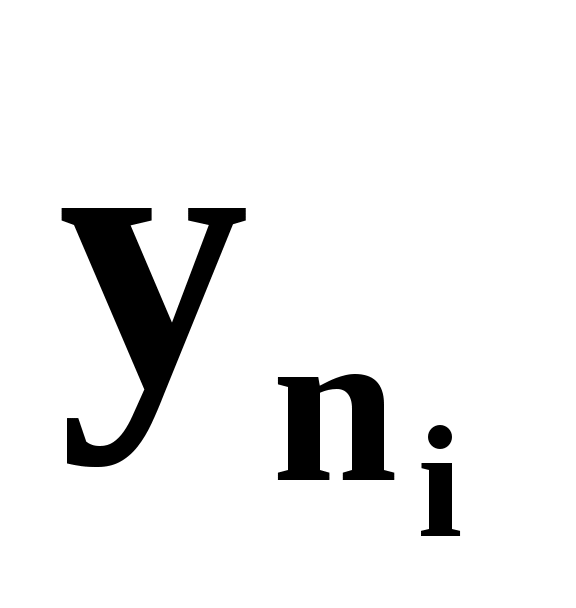
, и значения коэффициентов нестабильности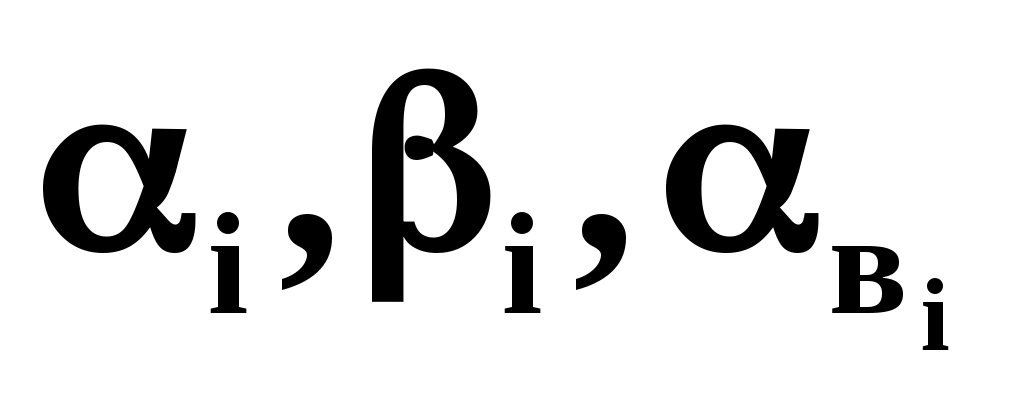
.
4. После проведения N расчетов получаем N случайных значений параметра у.
Дальнейшая обработка полученных данных заключатся в проведении вычислений и графическом представлении результатов.
Среднее значение параметра у рассчитывается по формуле
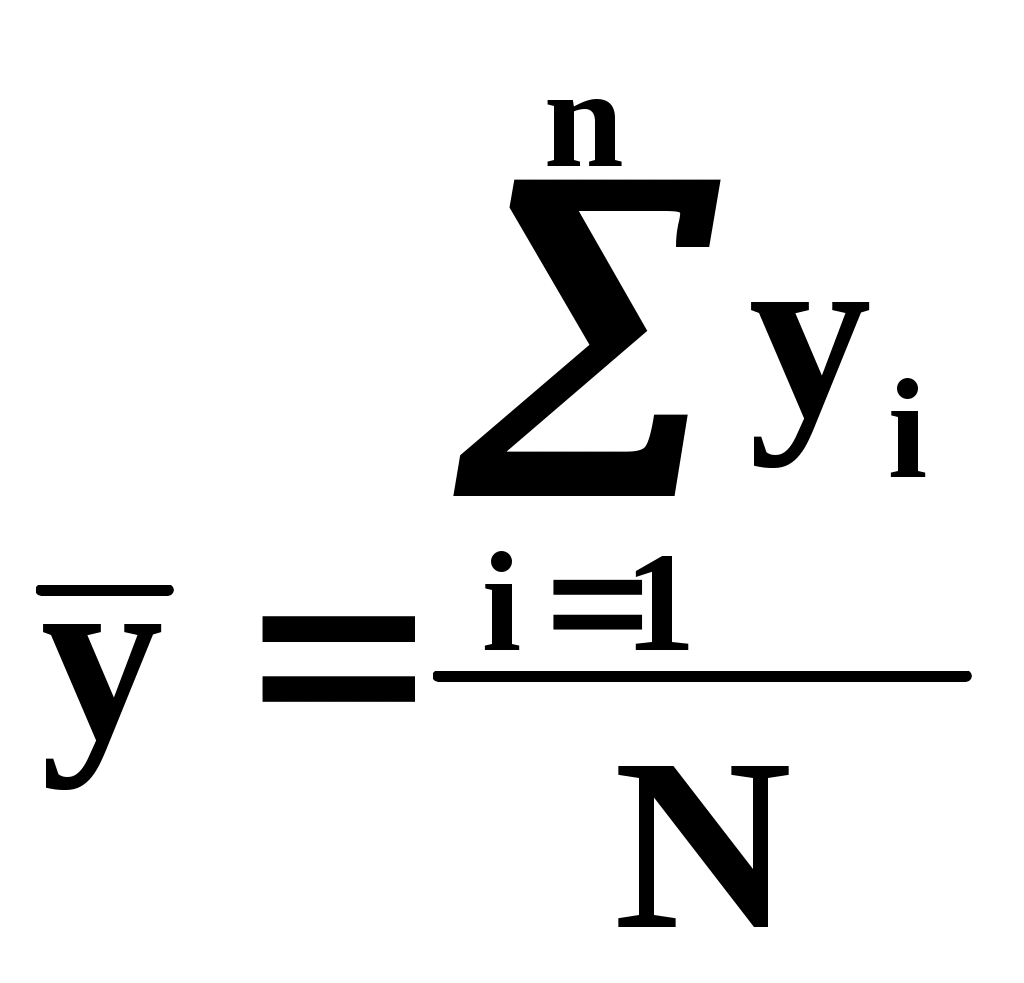
При работе с выборками конечного объема для оценки отклонения среднего значения параметра у пользуются понятием выборочного среднеквадратического отклонения Sy.
Выборочное среднеквадратическое отклонение Sy определяется из выражения
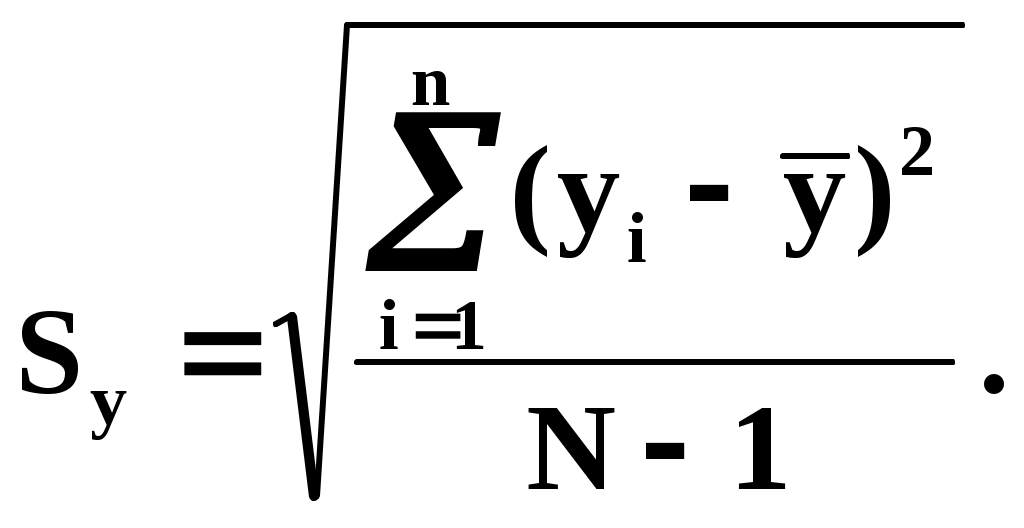
В предположении о нормальном законе распределения относительное предельное отклонение параметра у под влиянием дестабилизирующих факторов рассчитывается из соотношения
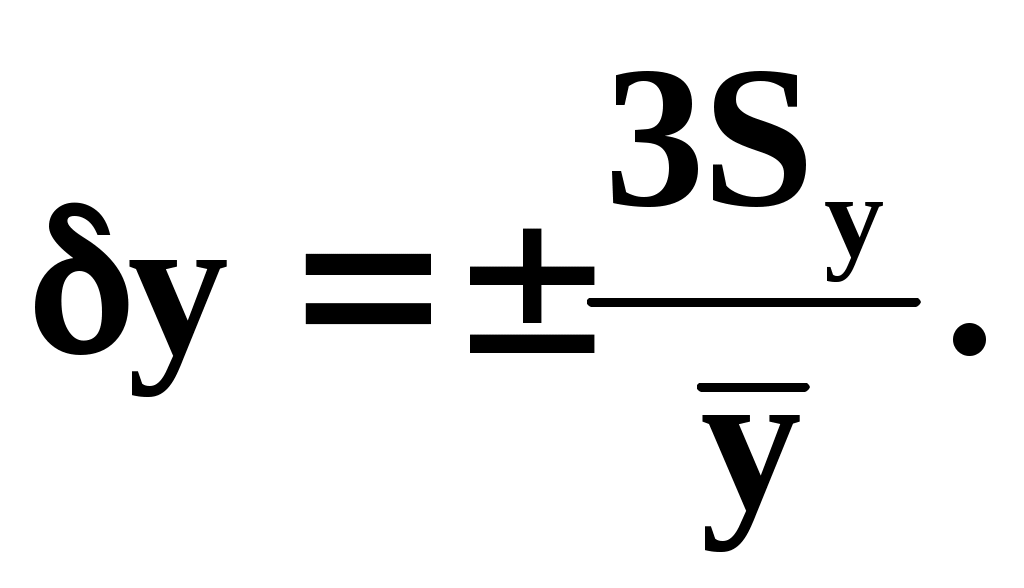
Абсолютное изменение величины предельного отклонения параметра (у) можно оценить по формуле
(у) = у - уTУ ,
где уTУ - половина границы поля допуска параметра по ТУ.
Для оценки доли радиокомпонентов, пригодных к дальнейшей эксплуатации, следует построить гистограмму распределения параметра у.
Для определения доли радиокомпонентов, пригодных к дальнейшей эксплуатации, следует на гистограмме указать границы поля допуска радиокомпонентов по ТУ. Сумма относительных весов (частостей) соответствующих интервалов, оказавшихся внутри границ поля допуска по ТУ, даст значение вероятности попадания значений параметров радиокомпонентов в указанный диапазон.
Вычисление интегралов методом статистических испытаний
(или методом Монте-Карло).
Задачи, связанные с вычислением многократных интегралов, могут быть эффективно решены методом статистических испытаний, особенно в тех случаях, когда к точности результатов расчёта не предъявляются очень жёсткие требования. Рассмотрим простейший пример для случая одного измерения.
Пусть – непрерывная случайная величина, принимающая свои значения Хi в некоторой области на оси OX. Закон распределения задан плотностью вероятностей
f(Х) в . Рассмотрим задачу об определении вероятности попадания случайной величины в интервал с фиксированными границами a и b, содержащийся в . Если обозначить искомую вероятность P(ab)=Р, то она выражается в виде интеграла:
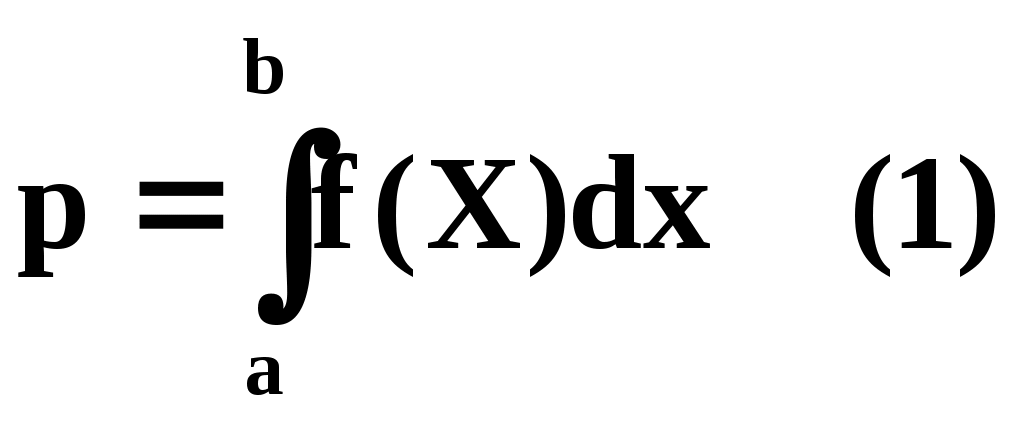
Этот интеграл можно вычислить по методу статистических испытаний (эксперимент с получением случайных значений Хi случайной величины ). Если появившееся при данном испытании значение Хi находится внутри интервала , данное испытание будем считать удачным. После проведения N испытаний подсчитаем число m удачных испытаний и вычислим частоту
попадания случайной величины в интервал :
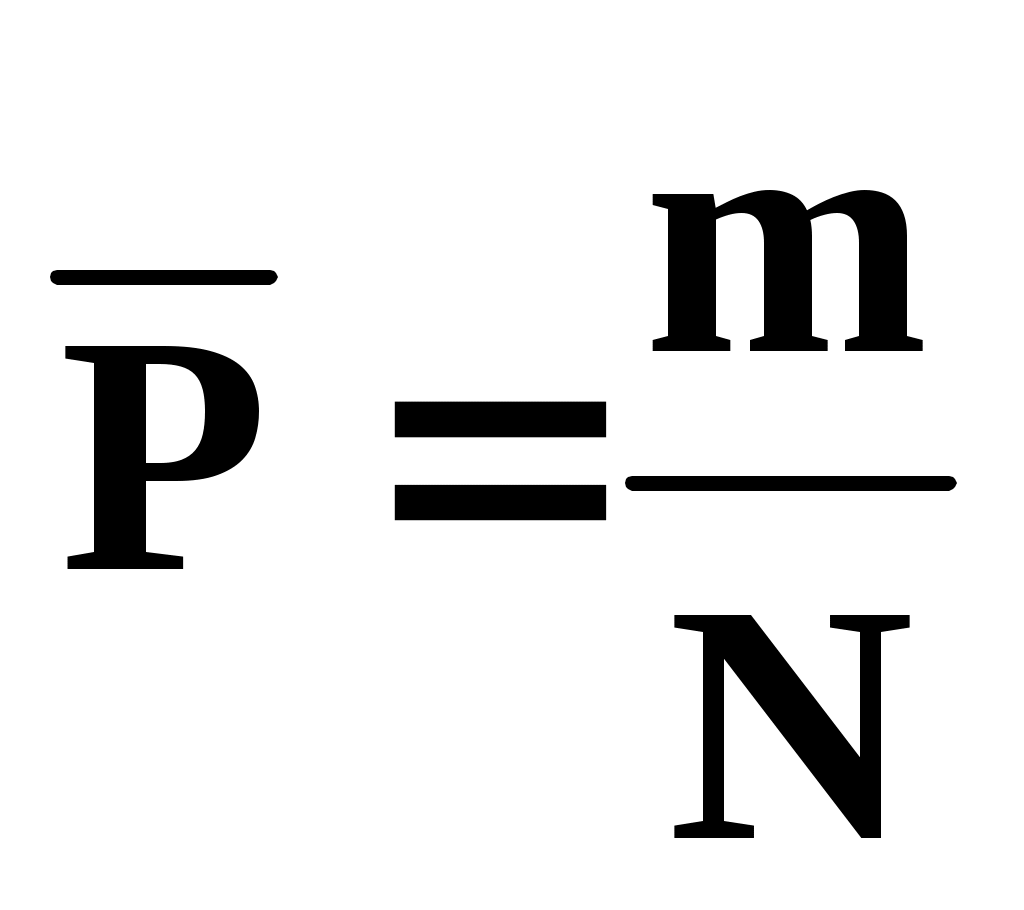. (2)
Располагая частотой , мы можем приближённо оценить искомую вероятность p на основании закона больших чисел.
Для этого воспользуемся теоремой Бернулли: если событие А имеет вероятность P и если m – число наступления событий А при N независимых испытаниях, то каково бы ни было постоянное 0
.
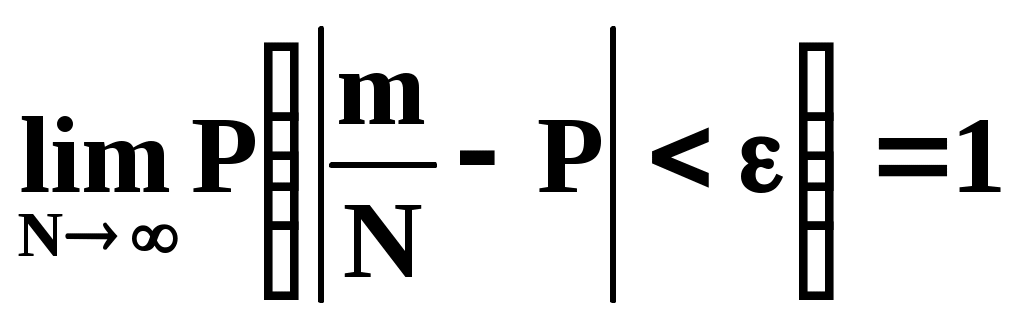При достаточно большом числе испытаний в качестве оценки для интеграла (1) можно взять частоту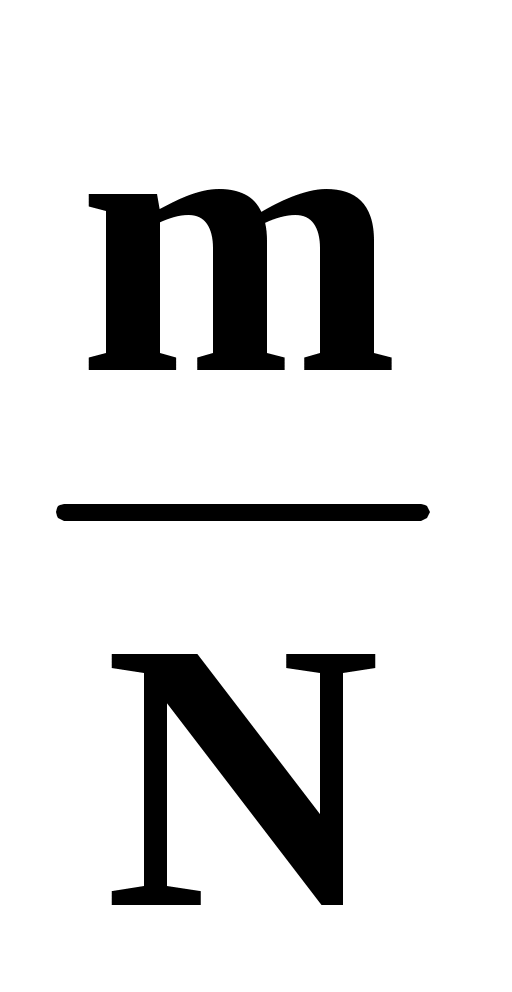
, т.е.
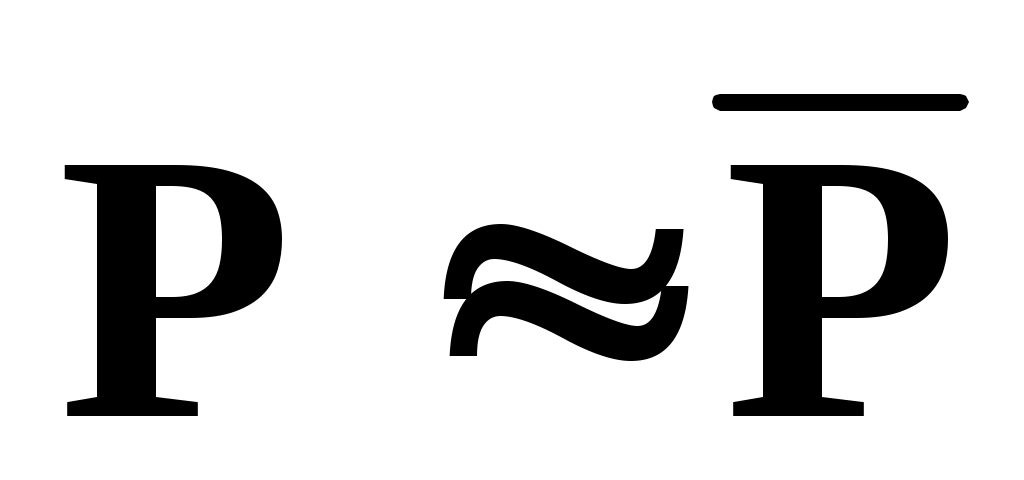. (3)
Моделирование эксперимента включает:
a Хi b; (4)
и равным нулю в противном случае;
Развитие вычислительной техники приводит к созданию программных комплексов, при использовании которых отпадает необходимость в программировании метода решения, т.е. достаточно лишь ограничиться заданием исходной информации. Это существенно снижает требования к знакомству пользователя ЭВМ с численными методами, но не устраняет полностью необходимости знакомства с вычислительным процессом.
Программные комплексы
мат. расчётов и моделирования
К числу современных пакетов прикладных программ (ППП), использующихся при мат. расчётах и моделировании, относятся: Scientific Work Place, Derive, MathCAD, Matematica, MatLAB и др. Все ППП имеют общий и хорошо известный из опыта работы с текстовыми и графическими редакторами набор файловых операций, вставки и удаления фрагментов, настройки системы, обеспечение справочной информацией. В них предусмотрены арифметические и логические операции, вычисление алгебраических и тригонометрических функций, решение систем алгебраических и дифференциальных уравнений и т.д. Новое поколение интегрированных ППП освоило и символьную форму представления уравнений, которая позволяет осуществлять перестановки, проводить операции с полиномами, разлагать функции Тейлора, решать дифференциальные уравнения и т.д.
Перечисленные возможности реализуются и в численной форме, а также используются в комбинации, когда сложное выражение преобразуется аналитически. В состав ППП входят также графические средства представления расчётов. Использование графических средств очень полезно, т.к. наш глаз способен выделять структуры и тренды, незаметные из табличных данных, а также обнаруживать изменения во времени, которые могут привести к пониманию важных механизмов, лежащих в основе поведения объекта. Они могут вычерчиваться как на плоскости, так и в пространстве в различных системах координат (т.е. в декартовой, в полярной, в цилиндрической и в сферической).
Метод статистических испытаний (метод Монте-Карло)
Одной из разновидностей мат. моделирования как чистого эксперимента является моделирование стохастических процессов. Это метод статистических испытаний или метод Монте-Карло, названный по аналогии с игрой в рулетку во всемирно известном казино Монте-Карло в Монако. Метод основан на многократном моделировании процесса при случайных воздействиях со статистической обработкой результатов испытаний (т.е. моделирования).
Хотя наибольшую пользу выборочный метод Монте-Карло приносит при моделировании вероятностных ситуаций, он приложим также и к некоторым полностью детерминистским задачам, не имеющим аналитического решения .
В методе Монте-Карло данные предшествующего опыта вырабатываются искусственно путем использования некоторого генератора случайных чисел в сочетании с интегральной функцией распределения вероятностей для исследуемого процесса. Таким генератором может быть таблица, колесо рулетки, подпрограмма ЭВМ или какой-либо другой источник равномерно распределенных случайных чисел.
Подлежащее разыгрыванию распределение вероятностей может быть основано на эмпирических данных, извлекаемых из ранее сформированных записей, или на результатах последнего эксперимента, либо может представлять собой известное теоретическое распределение. Случайные числа используются для получения дискретного ряда случайных переменных, имитирующего результаты, которых можно было бы ожидать в соответствии с разыгрываемым вероятностным распределением.
Способ применения метода Монте-Карло по идее довольно прост. Чтобы получить искусственную случайную выборку из совокупности величин, описываемой некоторой функцией распределения вероятностей, следует:
1. Построить график или таблицу интегральной функции распределения на основе ряда чисел, отражающего исследуемый процесс (а не на основе ряда случайных чисел), причем значения случайной переменной процесса откладываются по оси абсцисс (х), а значения вероятности (от 0 до 1)—по оси ординат (y).
2. С помощью генератора случайных чисел выбрать случайное десятичное число (СЧ) в пределах от 0 до 1 (с требуемым числом разрядов).
3. Провести горизонтальную прямую от точки на оси ординат, соответствующей выбранному СЧ, до пересечения с кривой распределения вероятностей.
4. Опустить из этой точки пересечения перпендикуляр на ось абсцисс.
5. Записать полученное значение х. Далее оно принимается как выборочное значение.
6. Повторить шаги 2—5 для всех требуемых случайных переменных, следуя тому порядку, в котором они были записаны.
Метод статистического моделирования Монте-Карло применяется для исследования и анализа характеристик радиокомпонентов при значительных отклонениях параметров от их средних значений (например, в программах Pspice, Electronics Workbench, и др.). Следует отметить, что в случае больших отклонений
хi входных параметров применение приближенных расчетных формул, полученных при использовании вероятностно-статистического метода анализа точности, приводит к значительным погрешностям полученных результатов.
Применение метода Монте-Карло позволяет получить функцию распределения плотности вероятности параметров радиокомпонентов. По графику этой функции можно определить не только среднее значение выходного параметра, но и предельные отклонения параметра, а также вероятность попадания параметра в заданные границы поля допуска.
При использовании метода статистического моделирования исследованию может подвергаться любая аналитически заданная функция вида
y = f(x1, x2,…xn) .
Объем вычислений при этом существенно увеличивается и для расчетов используется ЭВМ.
В качестве примера исследуем методом Монте-Карло функцию, выражающую зависимость выходного параметра радиокомпонента у от комплексного воздействия дестабилизирующих факторов (температуры, времени, влажности):
где yн – номинальное значение параметра; y,T – температурный коэффициент; y,t – коэффициент старения; - коэффициент влажности.
Значениями дестабилизирующих факторов являются: T – изменение температуры; t – промежуток времени, для которого рассчитывается изменение параметра у; значение влажности окружающей среды, косвенно задаваемое через величину коэффициента влажности .
Значения дестабилизирующих факторов (T, t, и влажности) являются детерминированными, т.е. неслучайными величинами.
Сущность метода Монте-Карло для анализа отклонения параметров радиокомпонентов может быть выражена в виде следующего алгоритма:
1. Рассчитывается или задается объем выборки радиокомпонентов N, необходимый для обеспечения достаточной точности проведения расчетов.
2. Измеряется N значений исследуемого параметра yn радиокомпонента, а также определяется N значений входных параметров (в данном случае коэффициентов нестабильности).
3. В расчетную формулу случайным образом подставляются значения
, и значения коэффициентов нестабильности
. 4. После проведения N расчетов получаем N случайных значений параметра у.
Дальнейшая обработка полученных данных заключатся в проведении вычислений и графическом представлении результатов.
Среднее значение параметра у рассчитывается по формуле
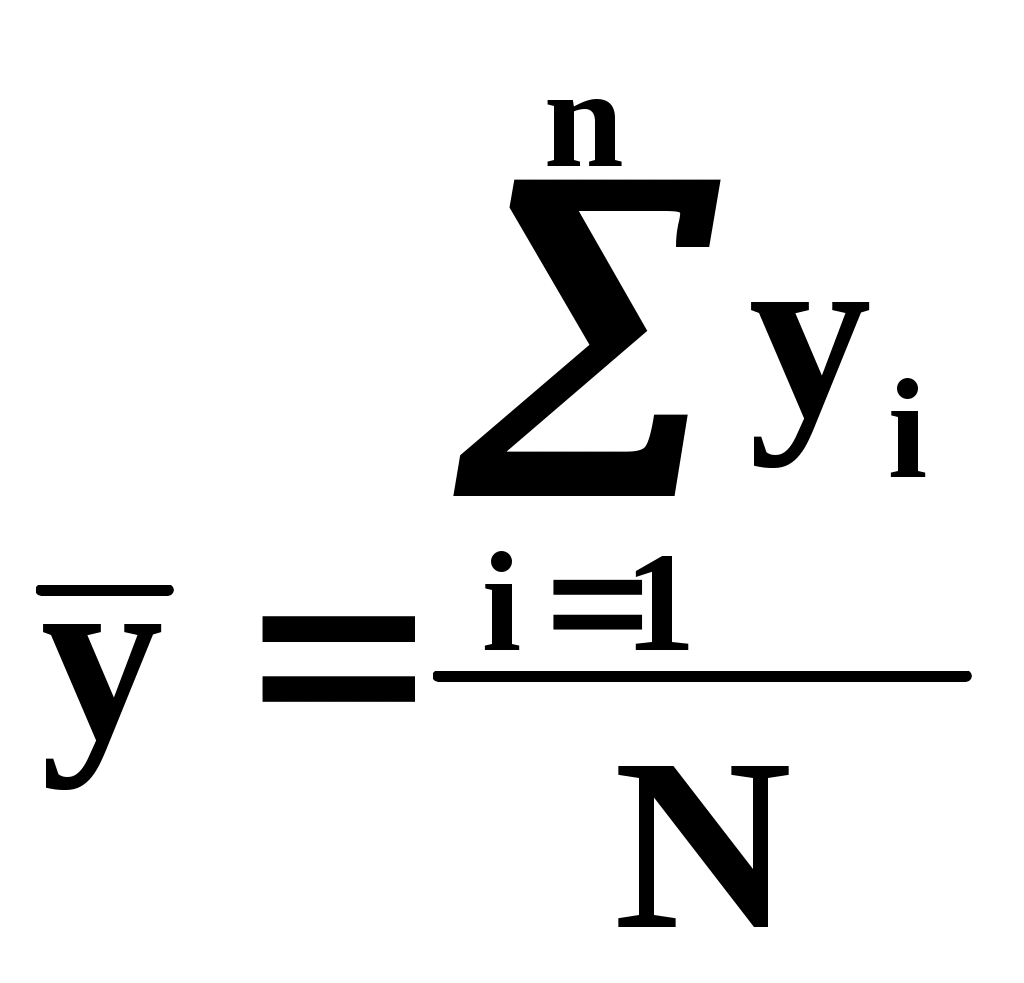
При работе с выборками конечного объема для оценки отклонения среднего значения параметра у пользуются понятием выборочного среднеквадратического отклонения Sy.
Выборочное среднеквадратическое отклонение Sy определяется из выражения
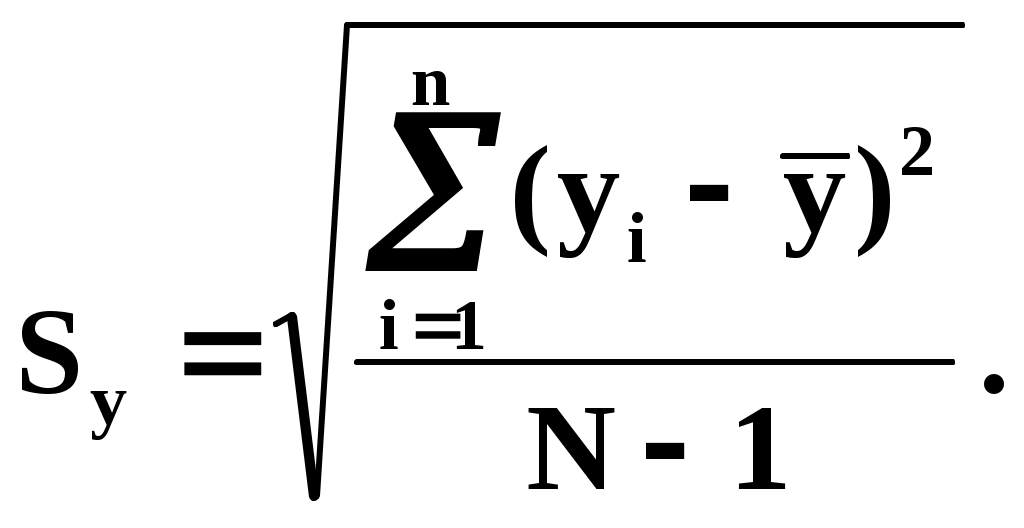
В предположении о нормальном законе распределения относительное предельное отклонение параметра у под влиянием дестабилизирующих факторов рассчитывается из соотношения
Абсолютное изменение величины предельного отклонения параметра (у) можно оценить по формуле
(у) = у - уTУ ,
где уTУ - половина границы поля допуска параметра по ТУ.
Для оценки доли радиокомпонентов, пригодных к дальнейшей эксплуатации, следует построить гистограмму распределения параметра у.
Для определения доли радиокомпонентов, пригодных к дальнейшей эксплуатации, следует на гистограмме указать границы поля допуска радиокомпонентов по ТУ. Сумма относительных весов (частостей) соответствующих интервалов, оказавшихся внутри границ поля допуска по ТУ, даст значение вероятности попадания значений параметров радиокомпонентов в указанный диапазон.
Вычисление интегралов методом статистических испытаний
(или методом Монте-Карло).
Задачи, связанные с вычислением многократных интегралов, могут быть эффективно решены методом статистических испытаний, особенно в тех случаях, когда к точности результатов расчёта не предъявляются очень жёсткие требования. Рассмотрим простейший пример для случая одного измерения.
Пусть – непрерывная случайная величина, принимающая свои значения Хi в некоторой области на оси OX. Закон распределения задан плотностью вероятностей
f(Х) в . Рассмотрим задачу об определении вероятности попадания случайной величины в интервал с фиксированными границами a и b, содержащийся в . Если обозначить искомую вероятность P(ab)=Р, то она выражается в виде интеграла:
Этот интеграл можно вычислить по методу статистических испытаний (эксперимент с получением случайных значений Хi случайной величины ). Если появившееся при данном испытании значение Хi находится внутри интервала , данное испытание будем считать удачным. После проведения N испытаний подсчитаем число m удачных испытаний и вычислим частоту
попадания случайной величины в интервал : . (2)Располагая частотой
, мы можем приближённо оценить искомую вероятность p на основании закона больших чисел.Для этого воспользуемся теоремой Бернулли: если событие А имеет вероятность P и если m – число наступления событий А при N независимых испытаниях, то каково бы ни было постоянное 0
.При достаточно большом числе испытаний в качестве оценки для интеграла (1) можно взять частоту
, т.е. . (3)Моделирование эксперимента включает:
-
из совокупности случайных чисел с законом распределения f(Х) извлекается число Хi; -
случайное число Хi сравнивается с границами a и b интервала . Результаты сравнения отмечаются специальным признаком , равным единице, если выполнено неравенство
a Хi b; (4)
и равным нулю в противном случае;
-
полученная величина прибавляется к содержимому «счётчика числа удачных испытаний»; -
к содержимому «счётчика количества испытаний» прибавляется единица.
