Файл: 1. Понятие матрицы. Виды матриц. Транспонирование матрицы. Равенство матриц. Алгебраические операции над матрицами умножение на число, сложение, умножение матриц.doc

.

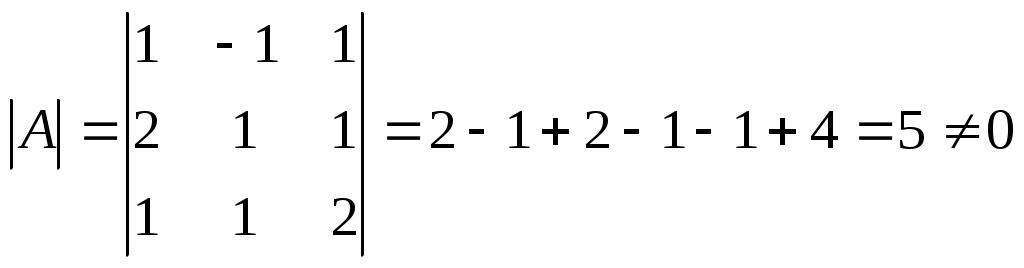2) Находим алгебраические дополнения элементов матрицы и составляем из них присоединенную матрицу :

.

3. 
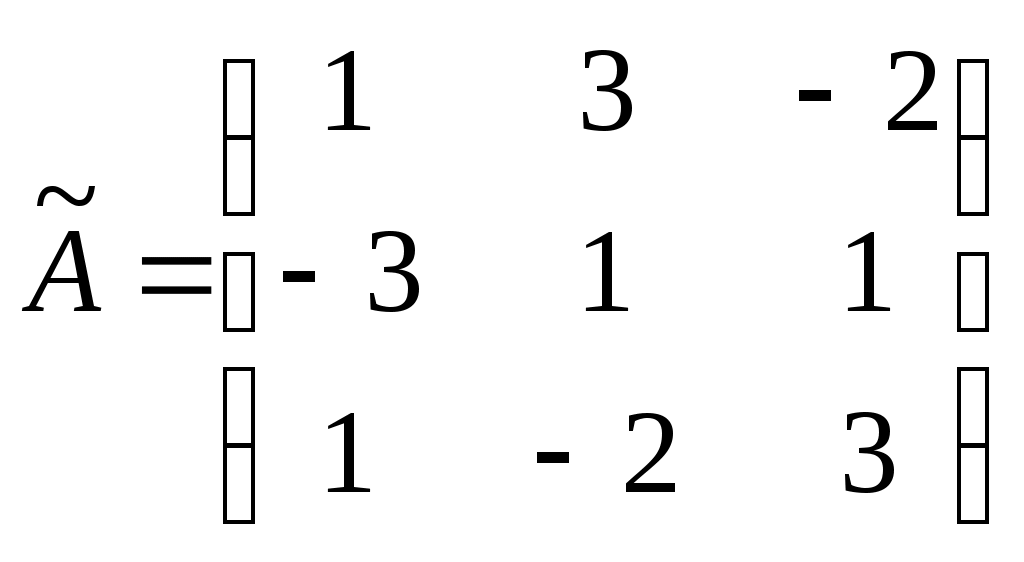   Вычисляем обратную матрицу:
   

,

4. 
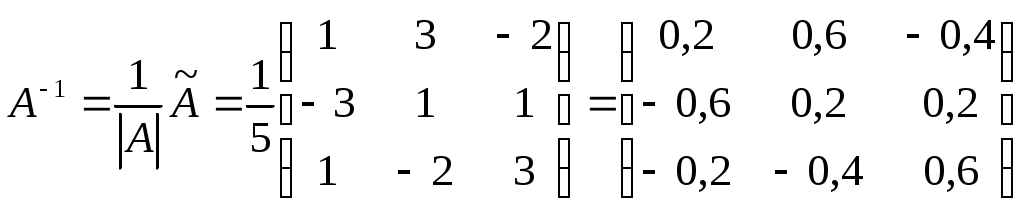   Проверяем:
   

.


4. Понятие минора k-го порядка. Ранг матрицы (определение). Вычисление ранга матрицы с помощью элементарных преобразований. Пример.

---

Ранг матрицы. Линейная независимость строк матрицы

Для решения и исследования ряда математических и прикладных задач важное значение имеет понятие ранга матрицы.

В матрице размером вычеркиванием каких-либо строк и столбцов можно вычленить квадратные подматрицы -го порядка, где . Определители таких подматриц называются минорами -го порядка матрицы .

Например, из матриц можно получить подматрицы 1, 2 и 3-го порядка.

Определение. Рангом матрицы называется наивысший порядок отличных от нуля миноров этой матрицы. Обозначение: или .

Из определения следует:

1) Ранг матрицы не превосходит меньшего из ее размеров, т.е. .

2) тогда и только тогда, когда все элементы матрицы равны нулю, т.е. .

3) Для квадратной матрицы n-го порядка тогда и только тогда, когда матрица - невырожденная.

Поскольку непосредственный перебор всех возможных миноров матрицы , начиная с наибольшего размера, затруднителен (трудоемок), то пользуются

---

элементарными преобразованиями матрицы, сохраняющими ранг матрицы.

Элементарные преобразования матрицы:

1. 
   Отбрасывание нулевой строки (столбца).
   
2. 
   Умножение всех элементов строки (столбца) на число .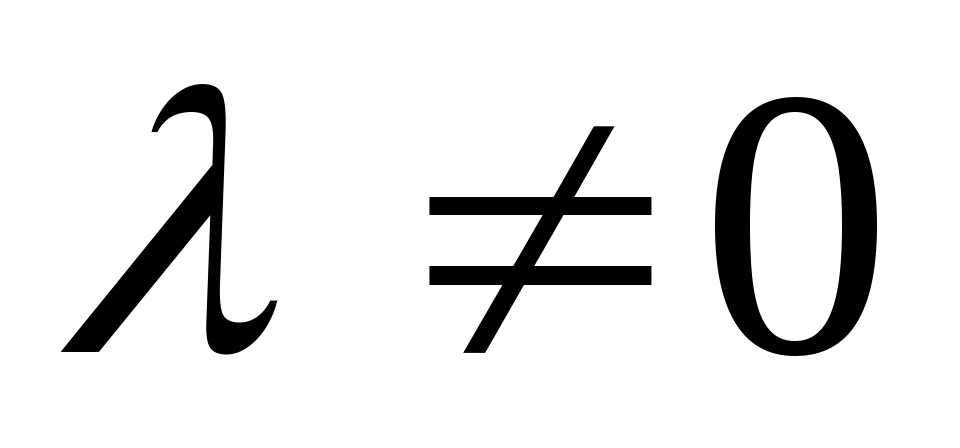
   
3. 
   Изменение порядка строк (столбцов) матрицы.
   
4. 
   Прибавление к каждому элементу одной строки (столбца) соответствующих элементов другой строки (столбца), умноженных на любое число.
   
5. 
   Транспонирование матрицы.
   

Определение. Матрица , полученная из матрицы при помощи элементарных преобразований, называется эквивалентной и обозначается А В.

Теорема. Ранг матрицы не изменяется при элементарных преобразованиях матрицы.

С помощью элементарных преобразований можно привести матрицу к так называемому ступенчатому виду, когда вычисление ее ранга не представляет труда.

Матрица называется ступенчатой если она имеет вид:

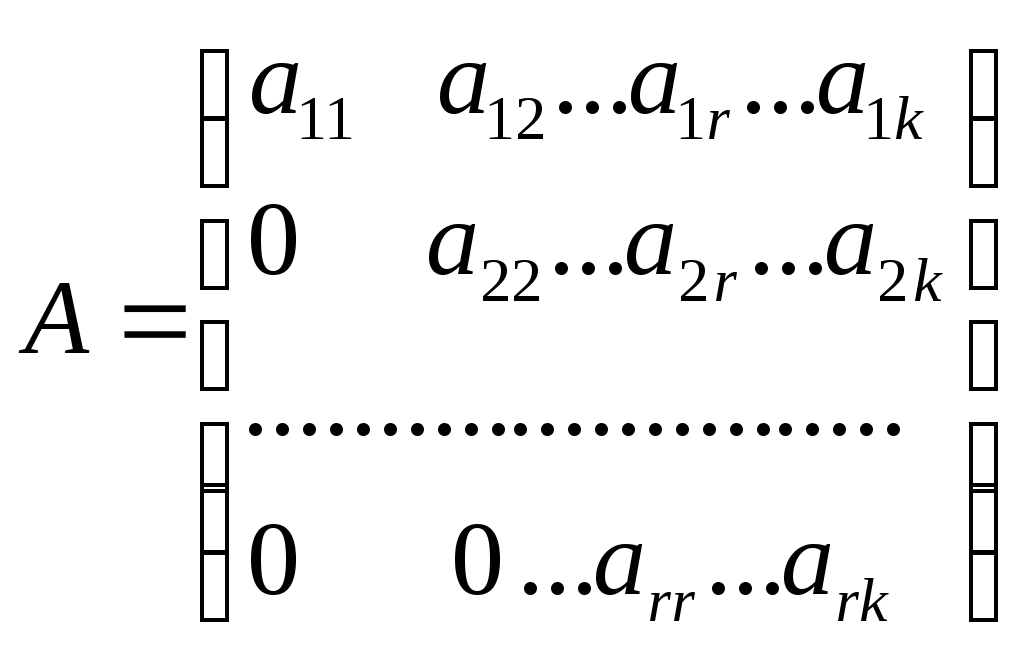, где , , .

Очевидно, что ранг ступенчатой матрицы равен числу ненулевых строк , т.к. имеется минор -го порядка, не равный нулю:

.

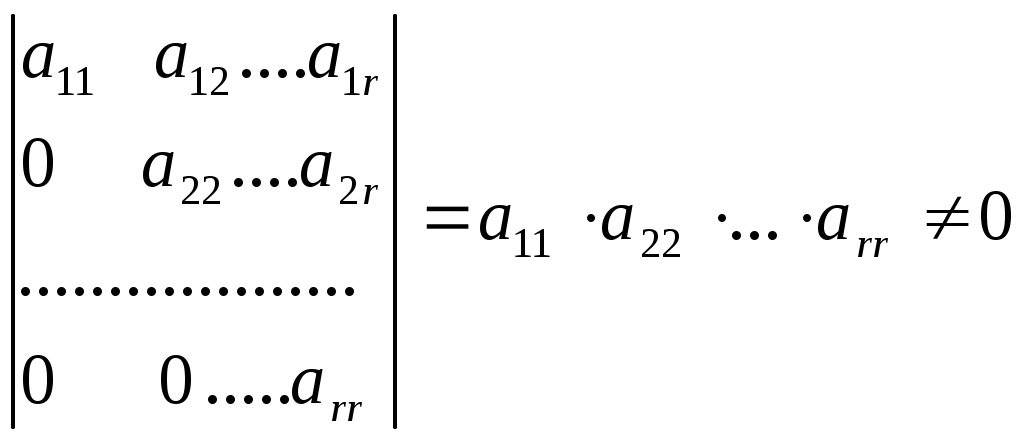Пример. Определить ранг матрицы с помощью элементарных преобразований.

---

.

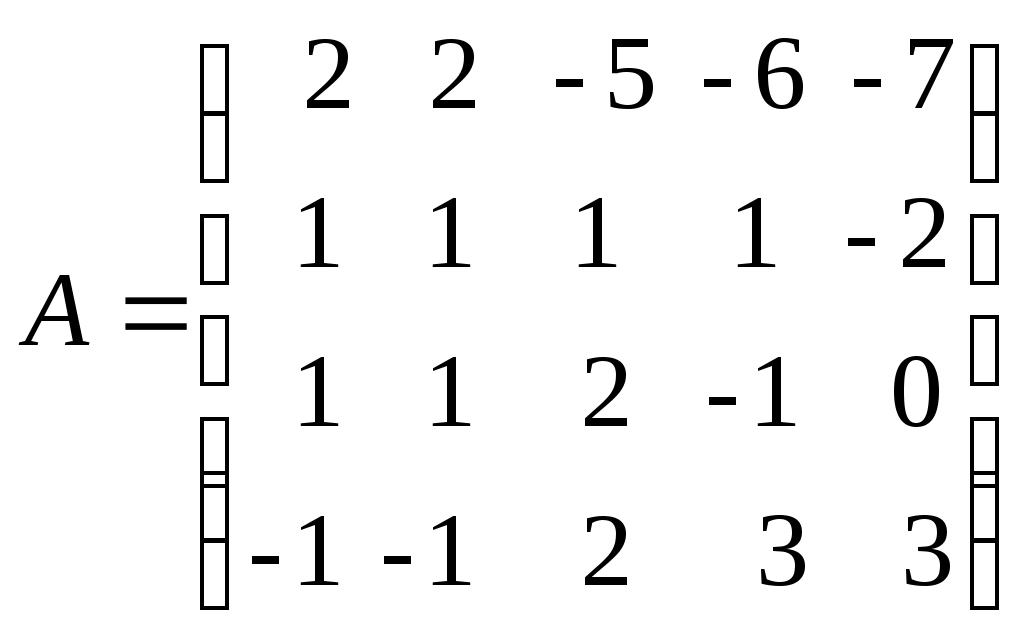
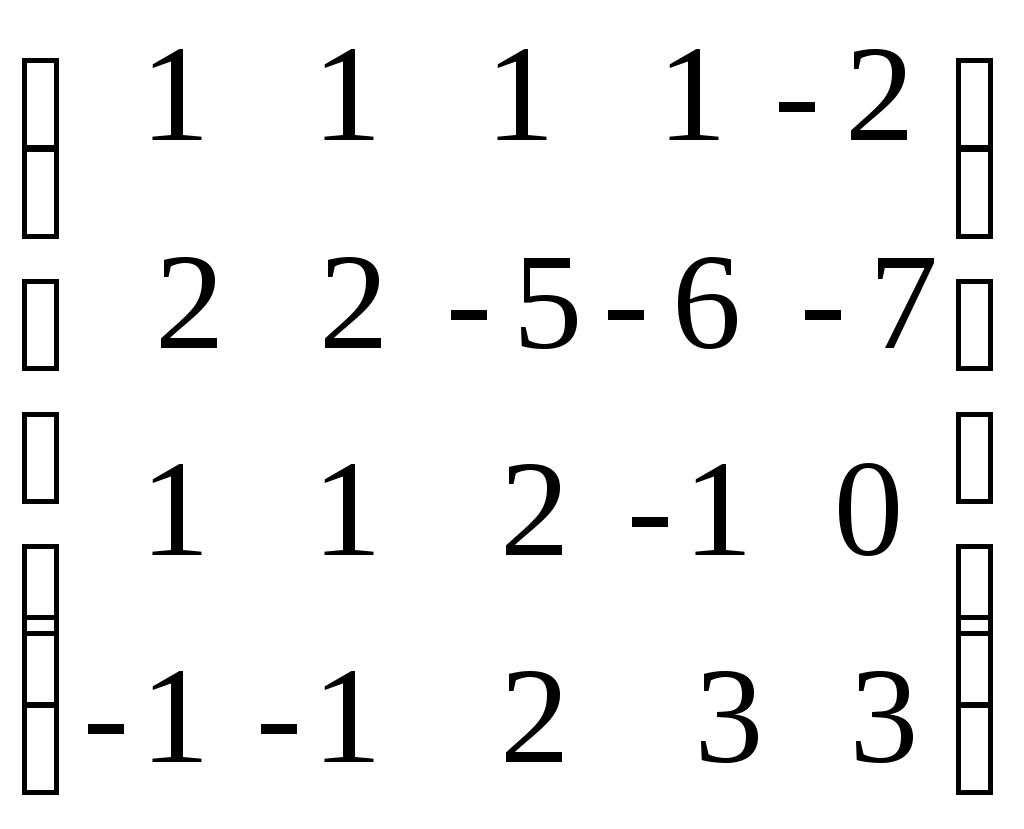
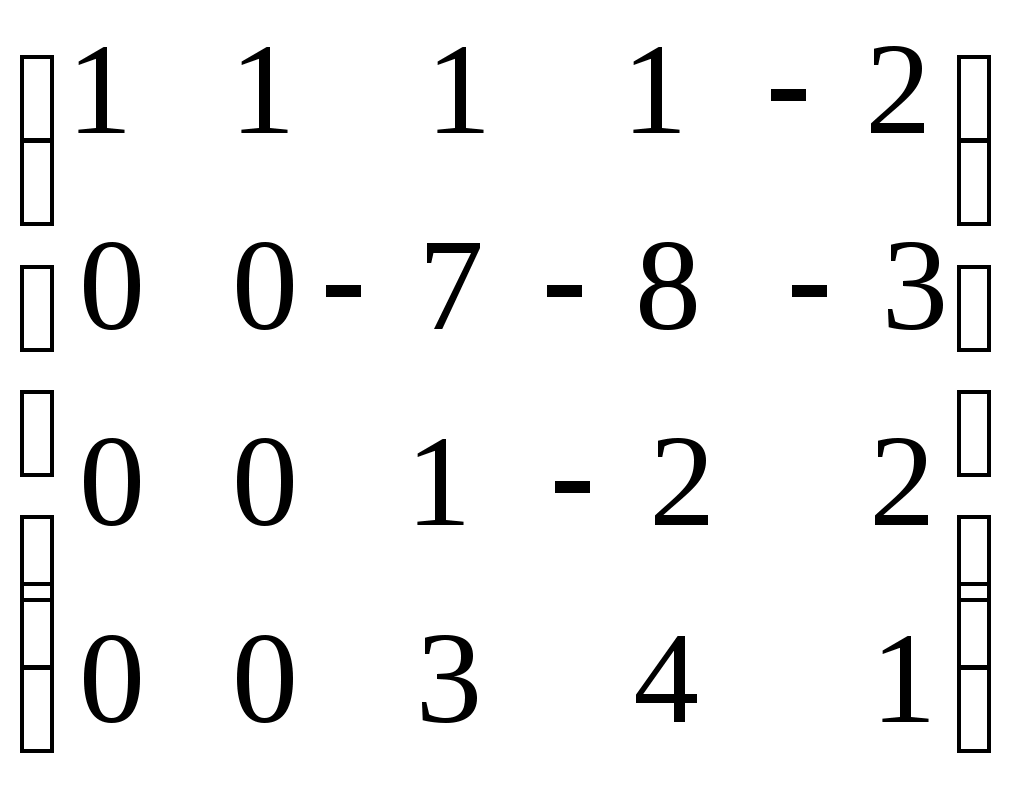
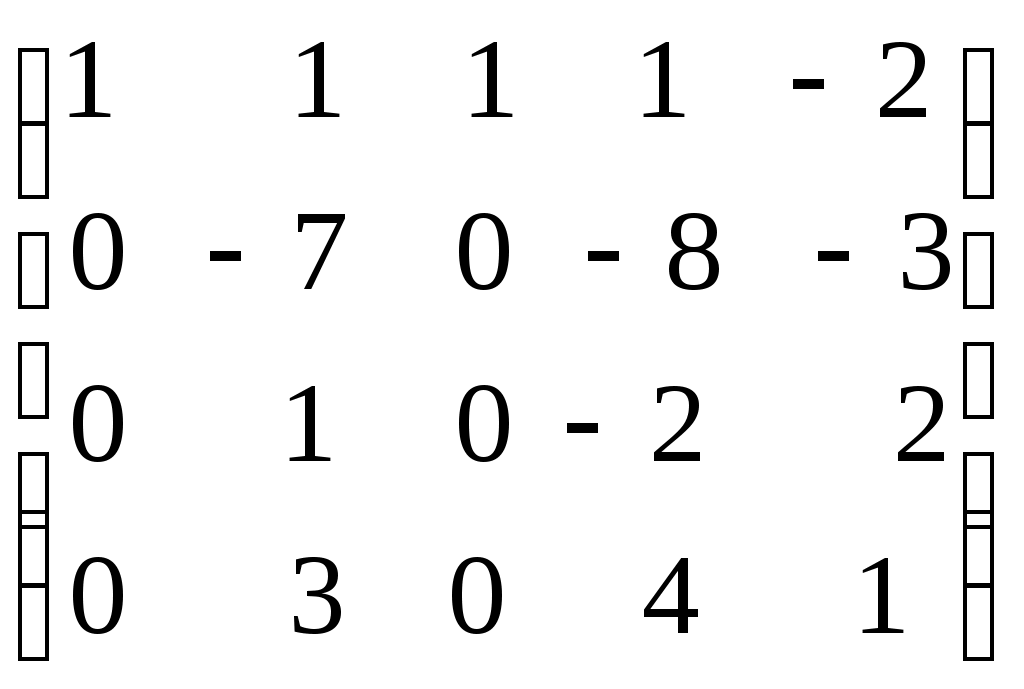
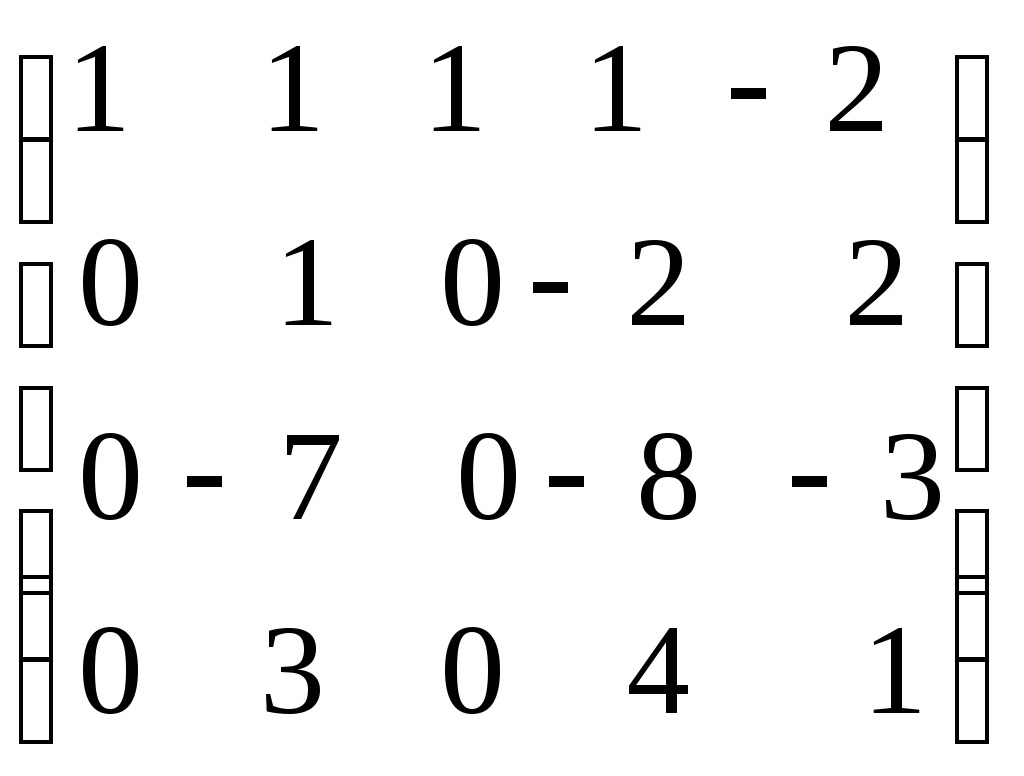
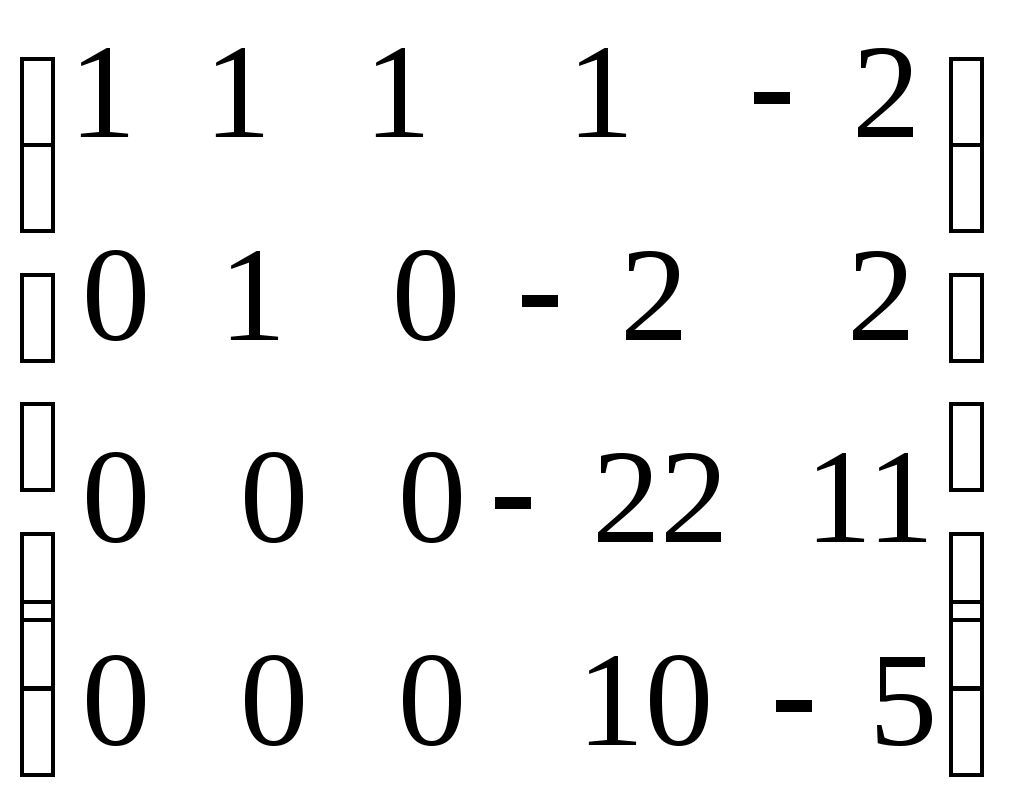
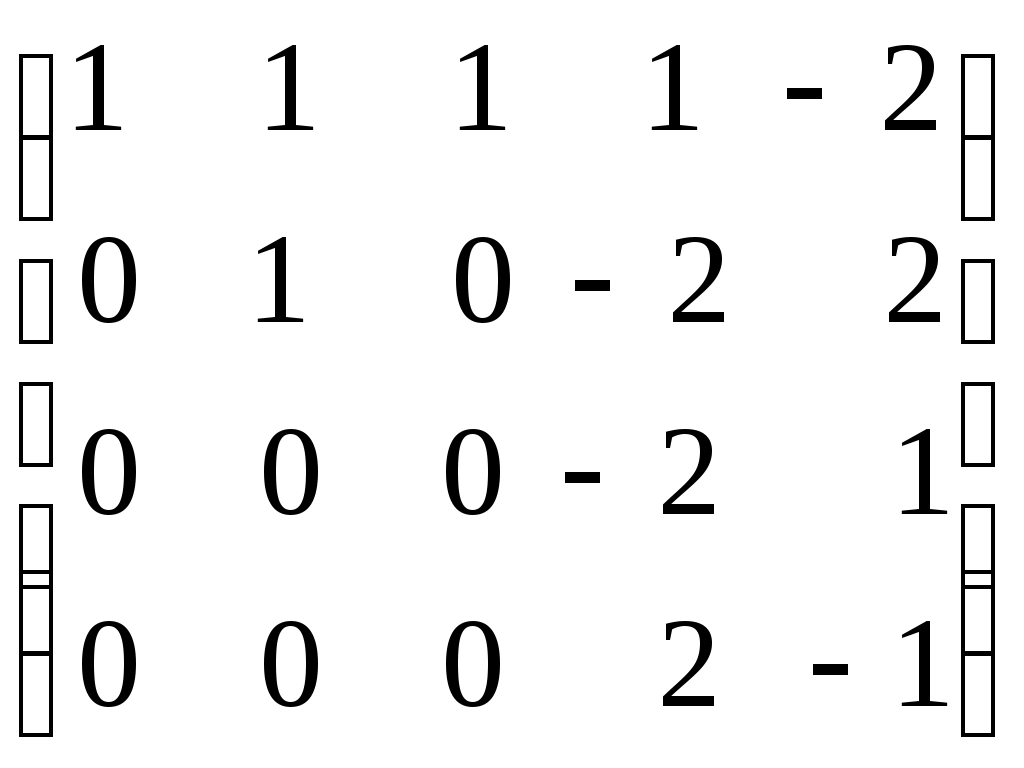
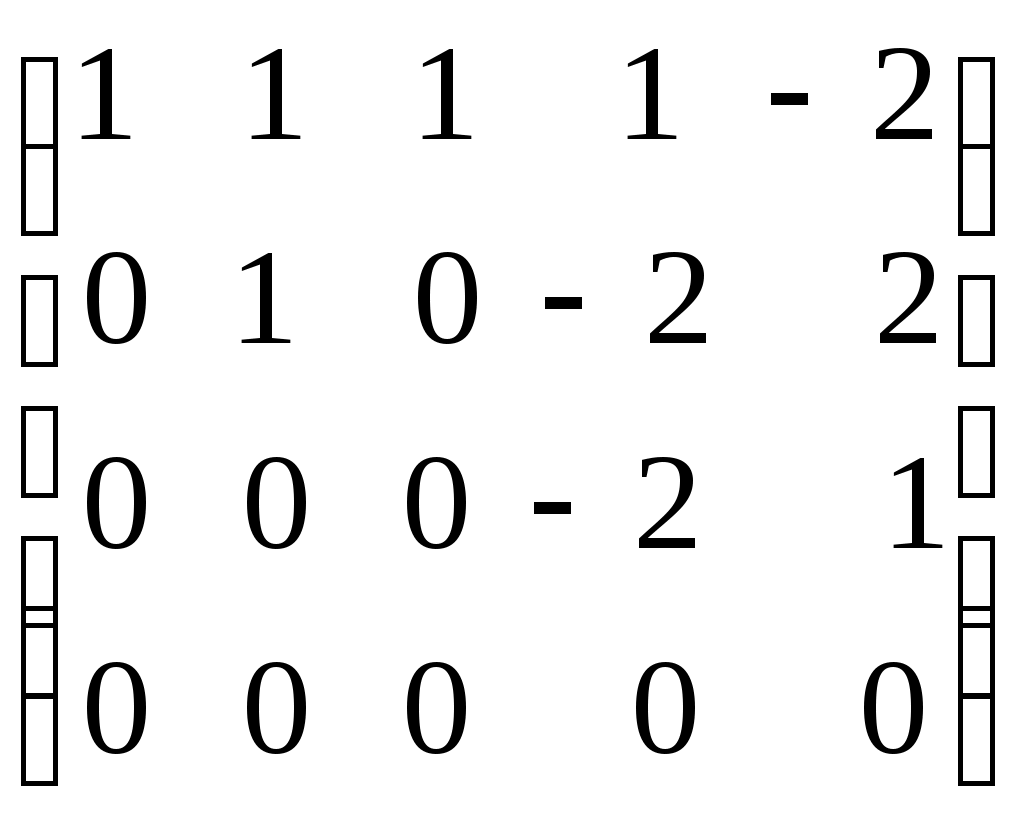
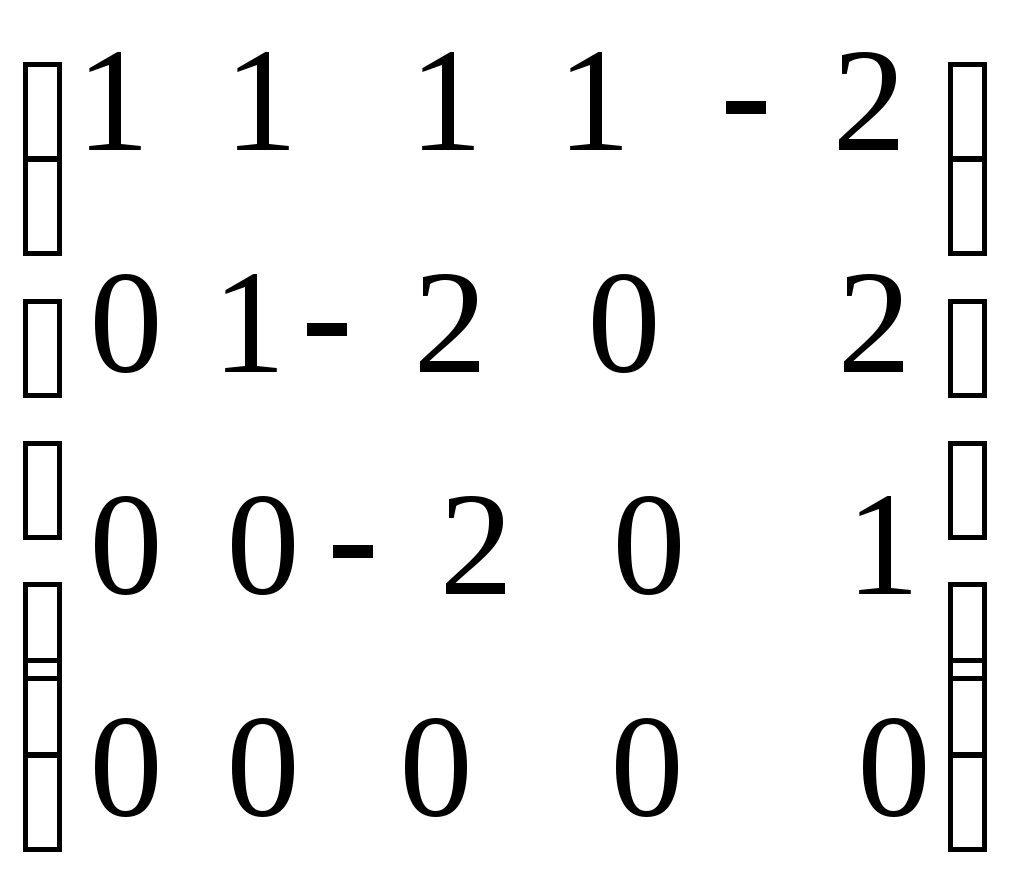Ранг матрицы равен количеству ненулевых строк, т.е. .

5. Линейная независимость столбцов (строк) матрицы. Теорема о ранге матрицы.

---

Линейная независимость строк матрицы

Дана матрица размера

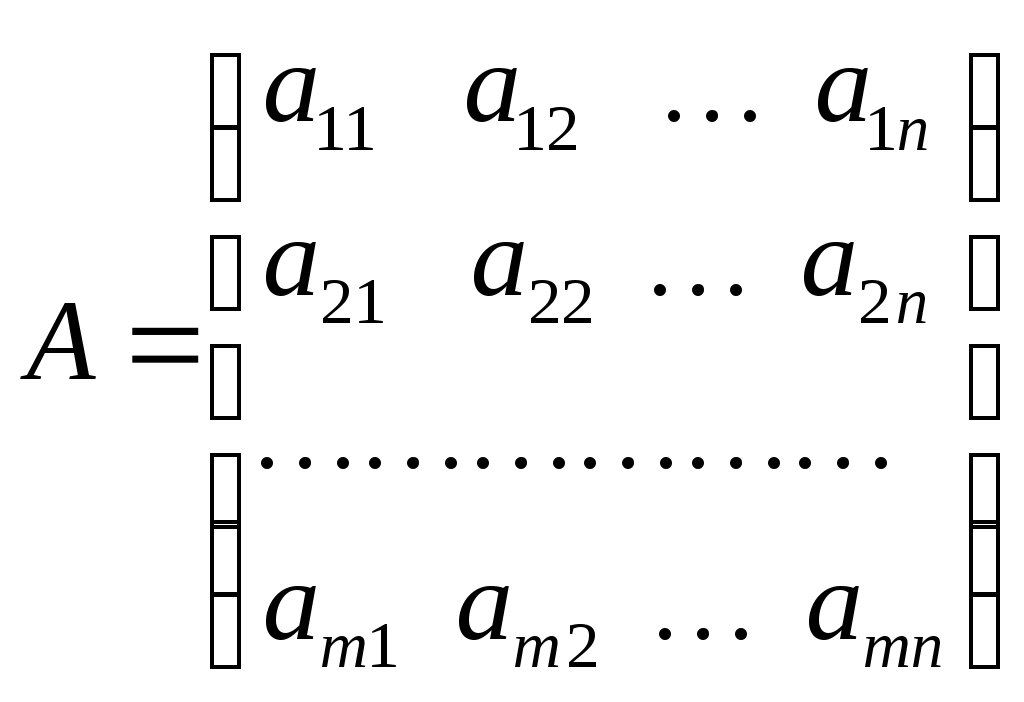
Обозначим строки матрицы следующим образом:



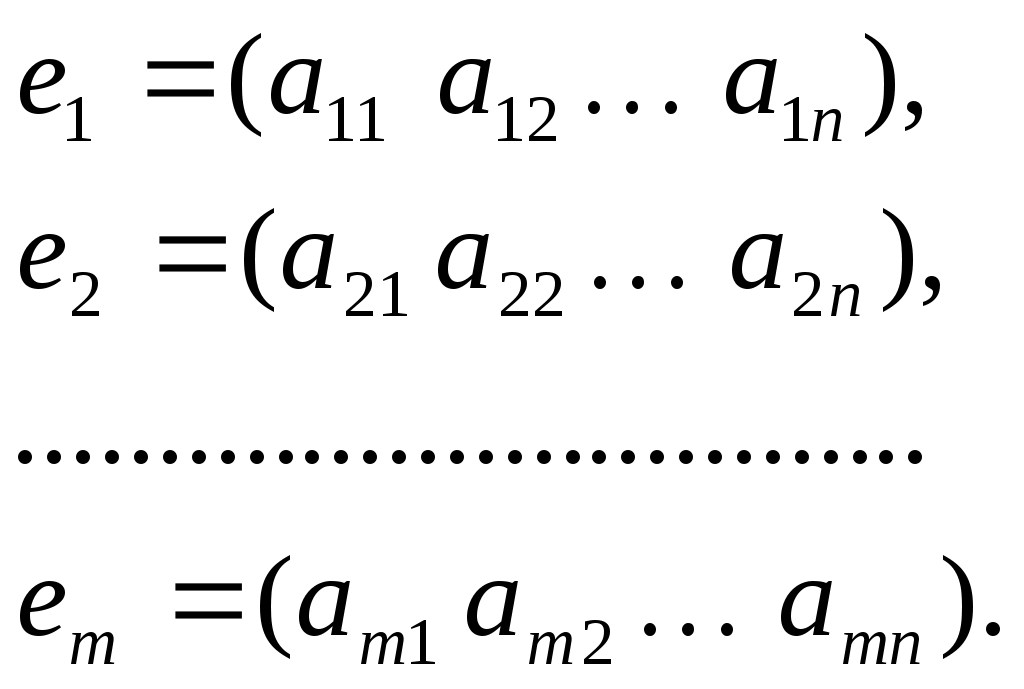
Две строки называются равными, если равны их соответствующие элементы. .

Введем операции умножения строки на число и сложение строк как операции, проводимые поэлементно:



.

Определение. Строка называется линейной комбинацией строк матрицы, если она равна сумме произведений этих строк на произвольные действительные числа (любые числа):

.

Определение. Строки матрицы называются линейно зависимыми, если существует такие числа , не равные одновременно нулю, что линейная комбинация строк матрицы равна нулевой строке:

, где . (1.1)

Линейная зависимость строк матрицы обозначает, что хотя бы 1 строка матрицы является линейной комбинацией остальных.

Определение. Если линейная комбинация строк (1.1) равна нулю тогда и только тогда, когда все коэффициенты , то строки называются линейно независимыми.

Теорема о ранге матрицы. Ранг матрицы равен максимальному числу ее линейно независимых строк или столбцов, через которые линейно выражаются все остальные строки (столбцы).

Теорема играет принципиальную роль в матричном анализе, в частности, при исследовании систем линейных уравнений.

---