Файл: 1. Понятие матрицы. Виды матриц. Транспонирование матрицы. Равенство матриц. Алгебраические операции над матрицами умножение на число, сложение, умножение матриц.doc

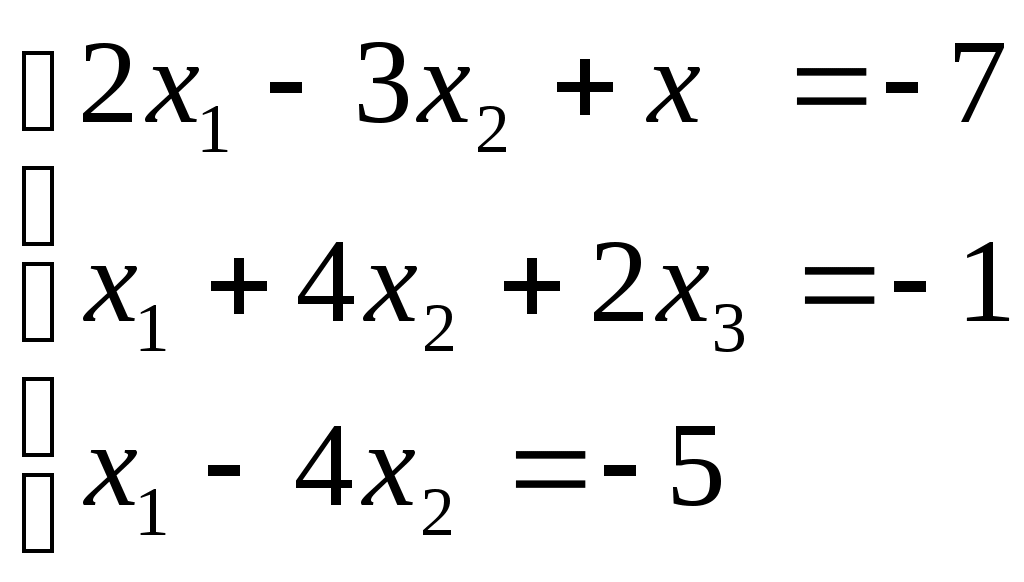
Выпишем расширенную матрицу системы.

Шаг 1. Поменяем местами первую и вторую строки, чтобы стал равным 1.

Шаг 2. Умножим элементы первой строки на (–2) и (–1) и прибавим их к элементам второй и третьей строк, чтобы под элементом в первом столбце образовались нули.

Шаг 3. Умножим элементы третьей строки на (–0,5).

Шаг 4. Поменяем местами вторую и третью строки.

Шаг 5. Поменяем местами второй и третий столбец. (Шаги 3, 4, 5 приведены с тем, чтобы ).

Шаг 6. Элементы второй строки умножим на 3 и прибавим их к элементам третьей строки, тогда под элементом появится нуль.

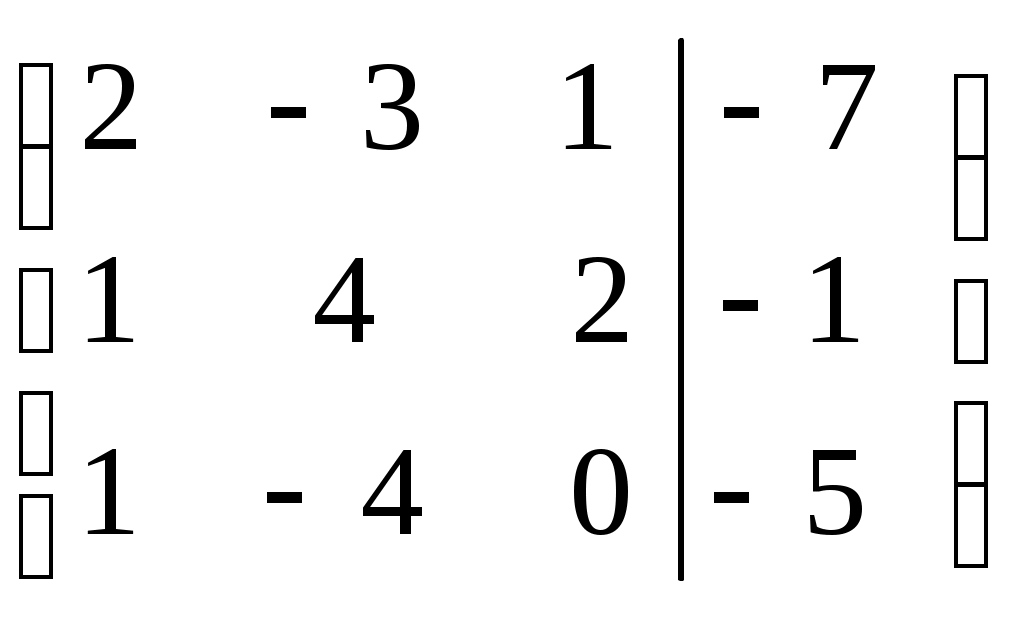(называется расширенная матрица системы) .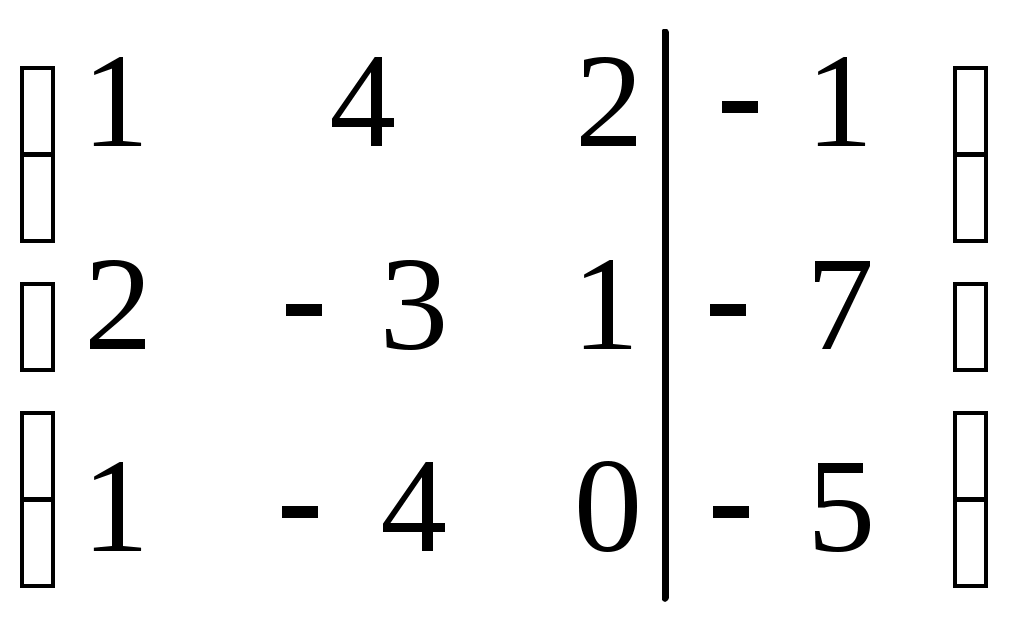

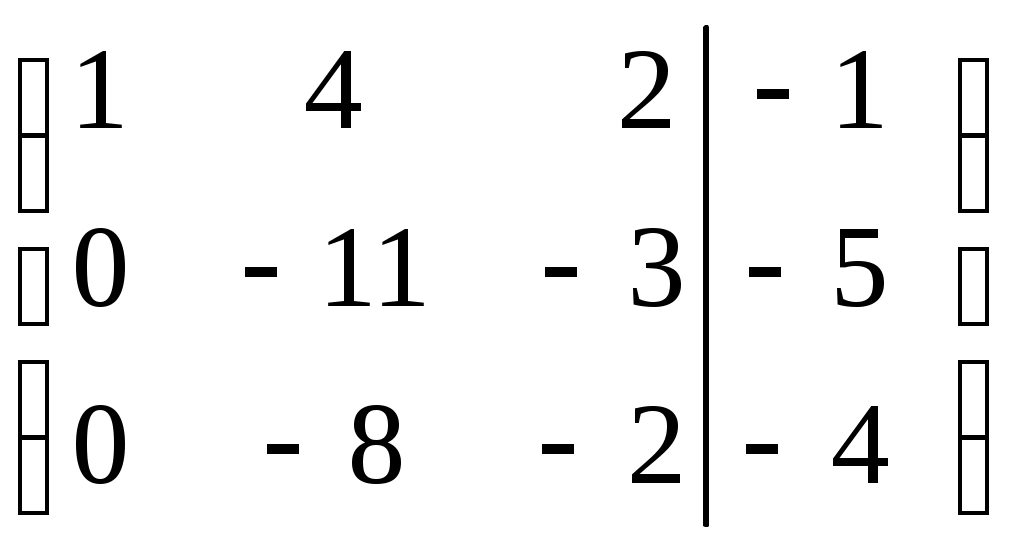
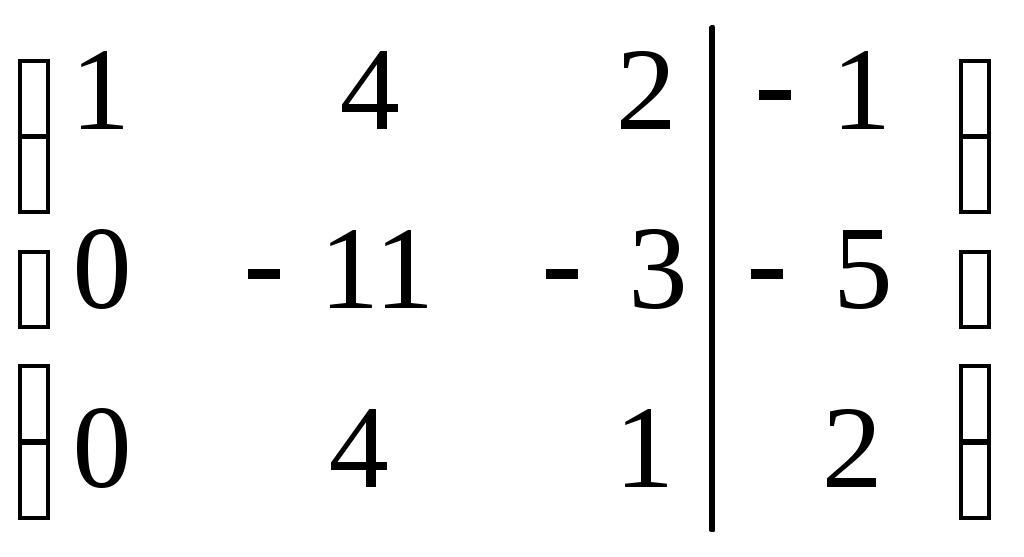
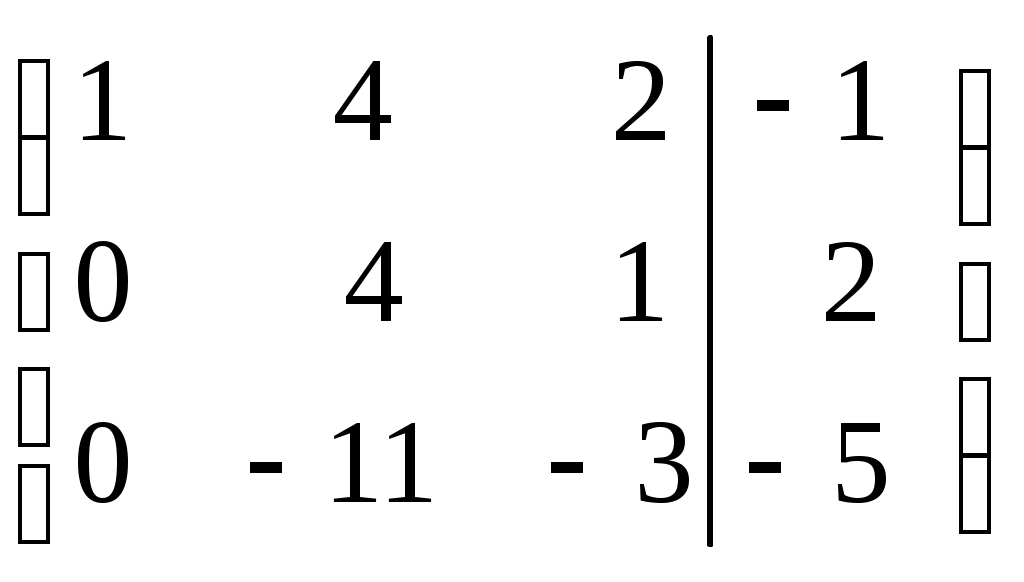
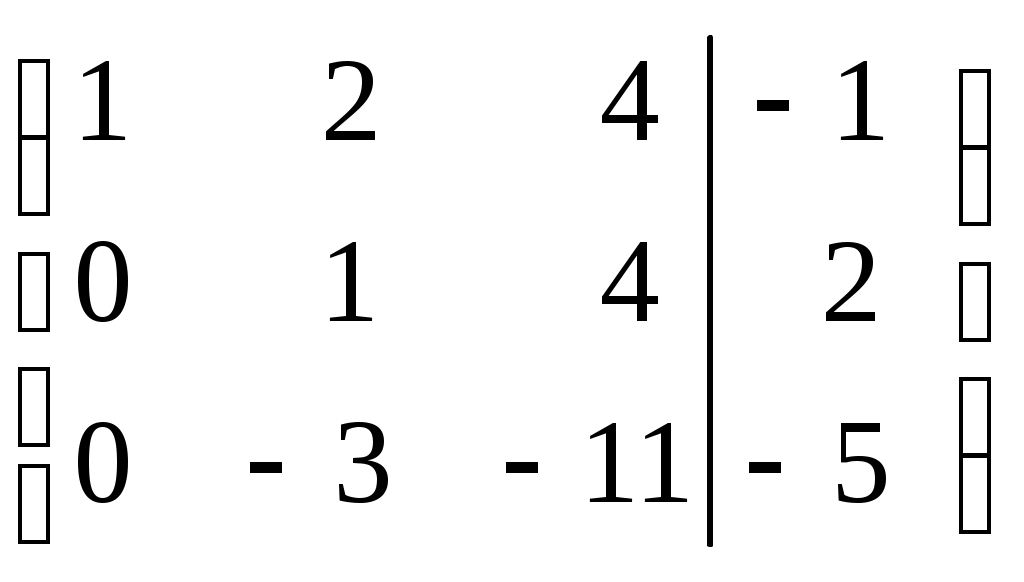
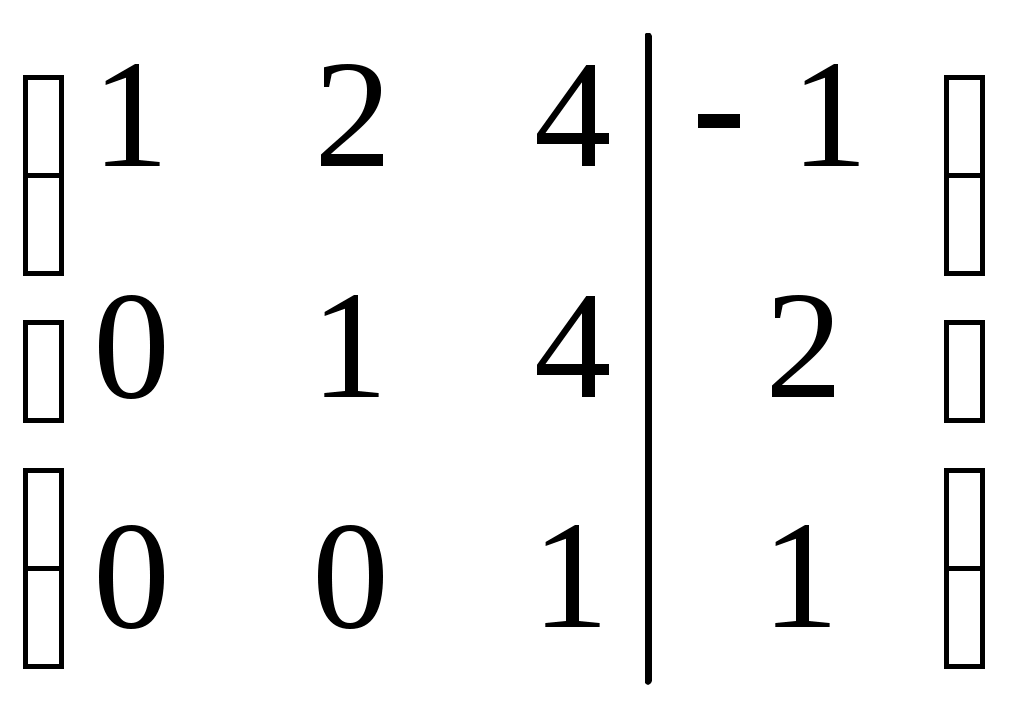Расширенная матрица приведена к треугольному виду. Соответствующая ей система имеет вид:



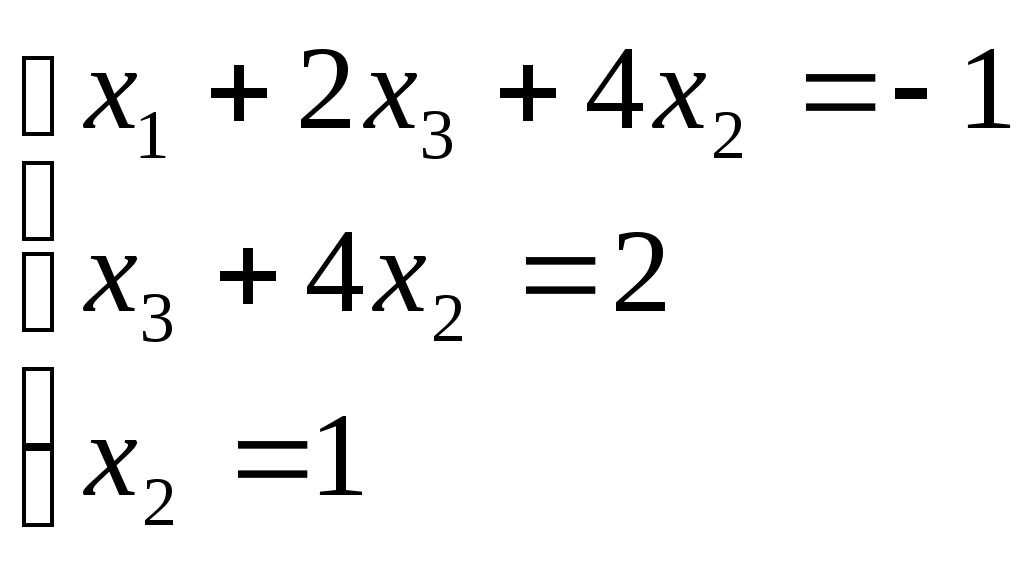
Из последнего уравнения ; из второго ; из первого .

Таким образом, ,

---

, .

10. Решение систем п линейных уравнений с п переменными с помощью обратной матрицы (вывод формулы Х=А ^–1В).

Для получения решения системы 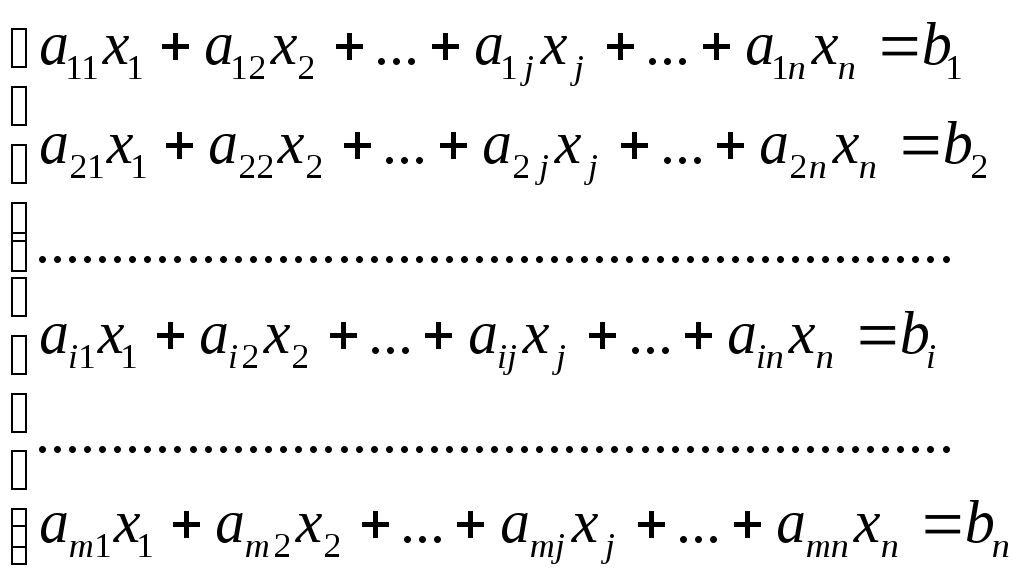при в общем виде предположим, что квадратная матрица системы невырожденная, т.е. ее определитель . В этом случае существует обратная матрица .

Метод обратной матрицы.

Запишем систему в матричной форме:

, где

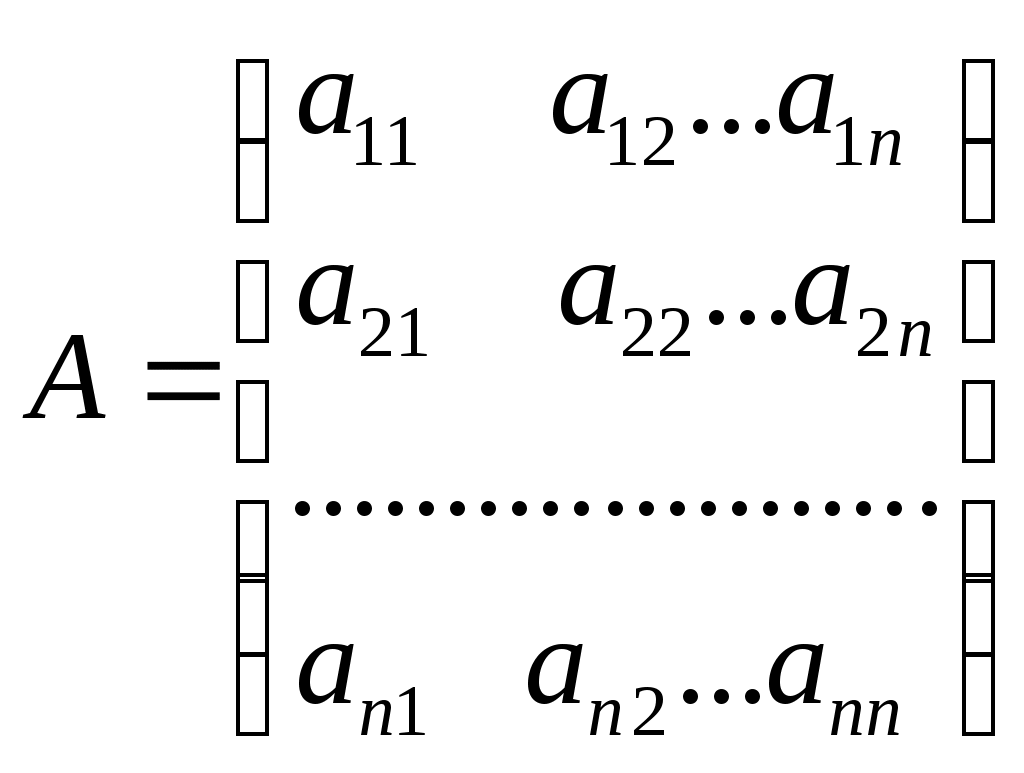- матрица коэффициентов при переменных,

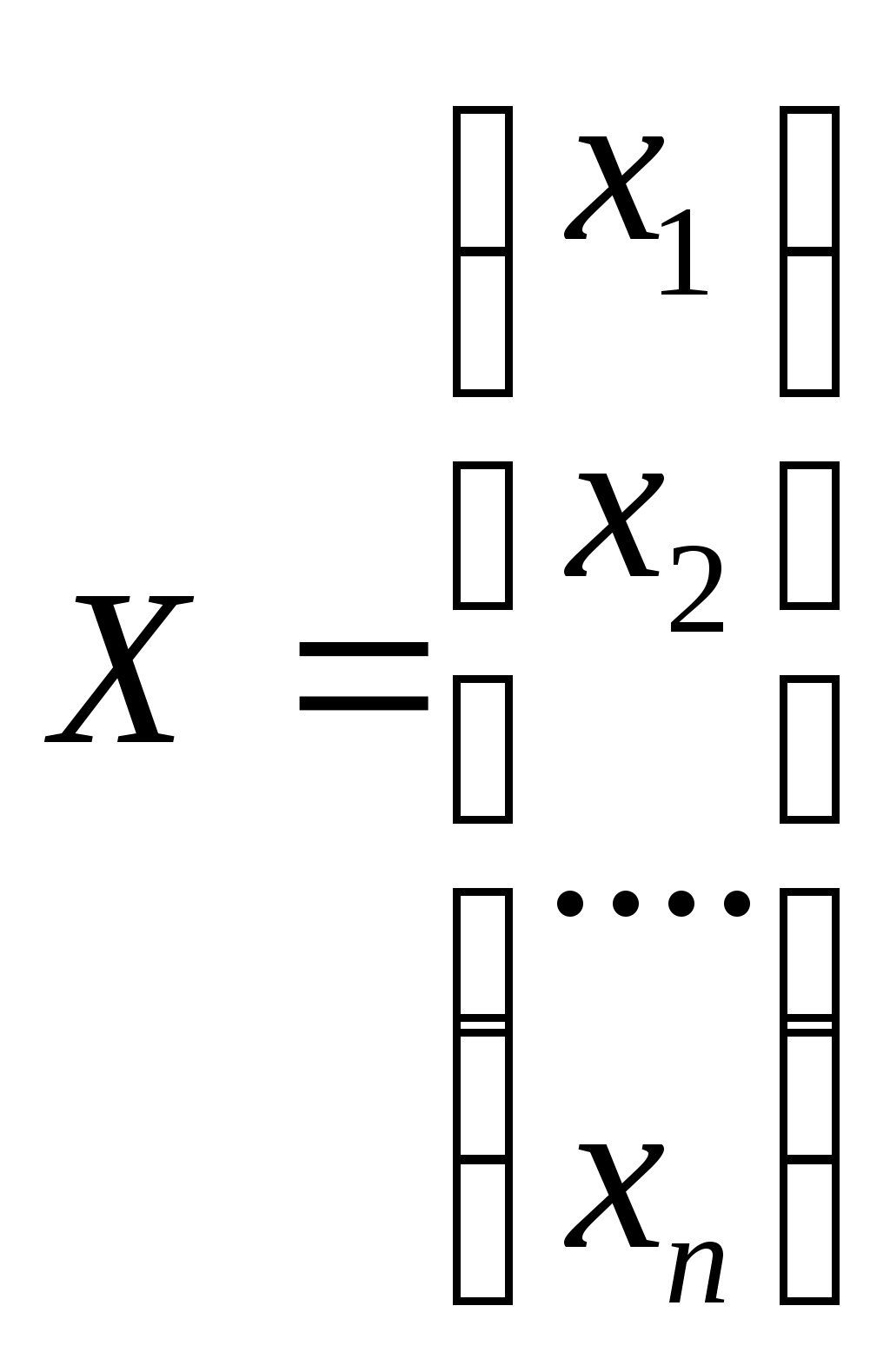- матрица-столбец переменных; 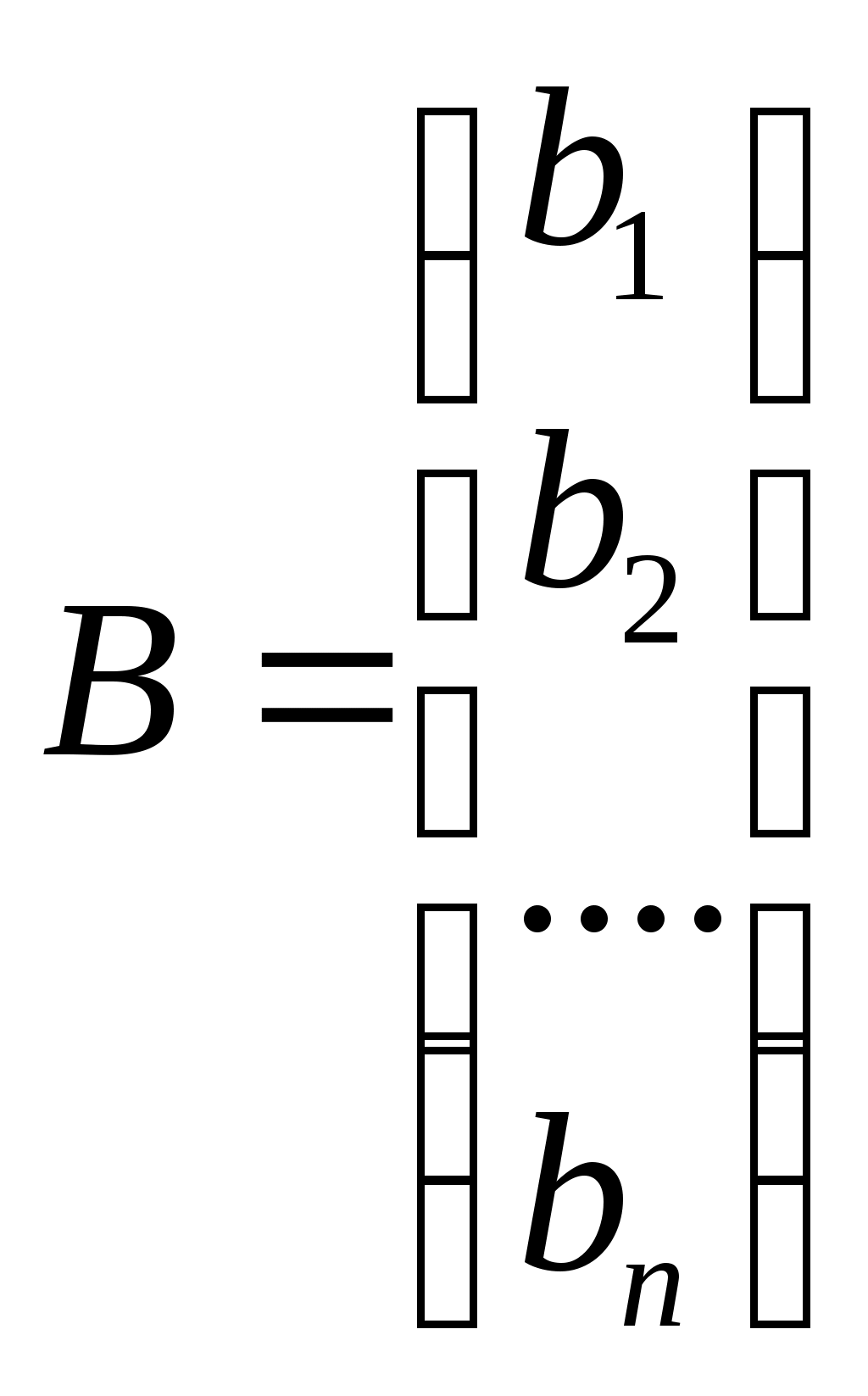- матрица столбец свободных членов.
Умножим слева обе части равенства на матрицу :

;

;

;

.

Таким образом, решение системы в матричном виде .

Пример. Решить систему уравнений методом обратной матрицы.

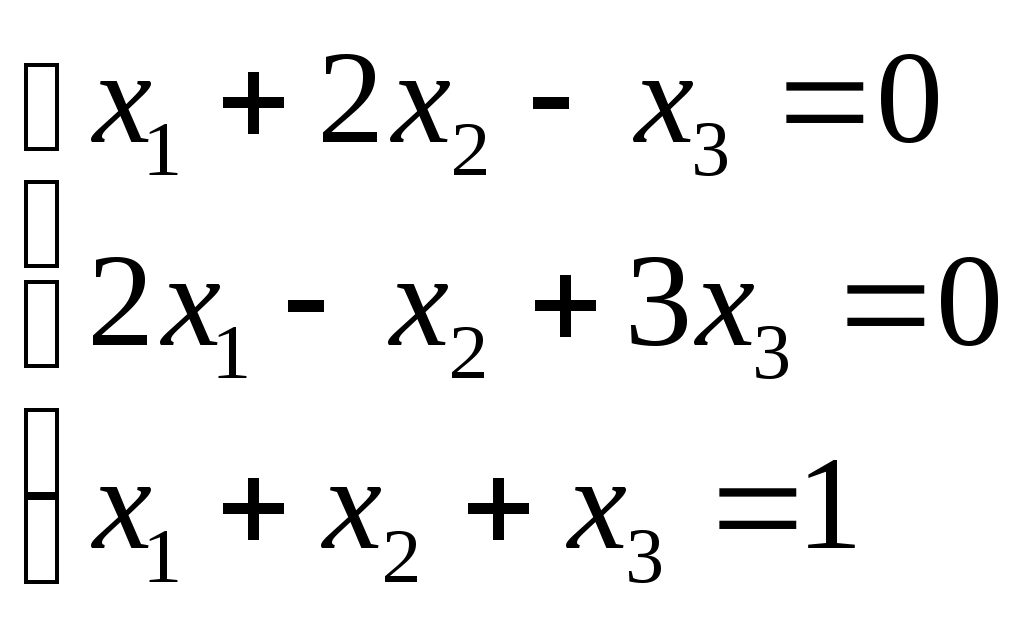
Р е ш е н и е: Обозначим ;

---

; .

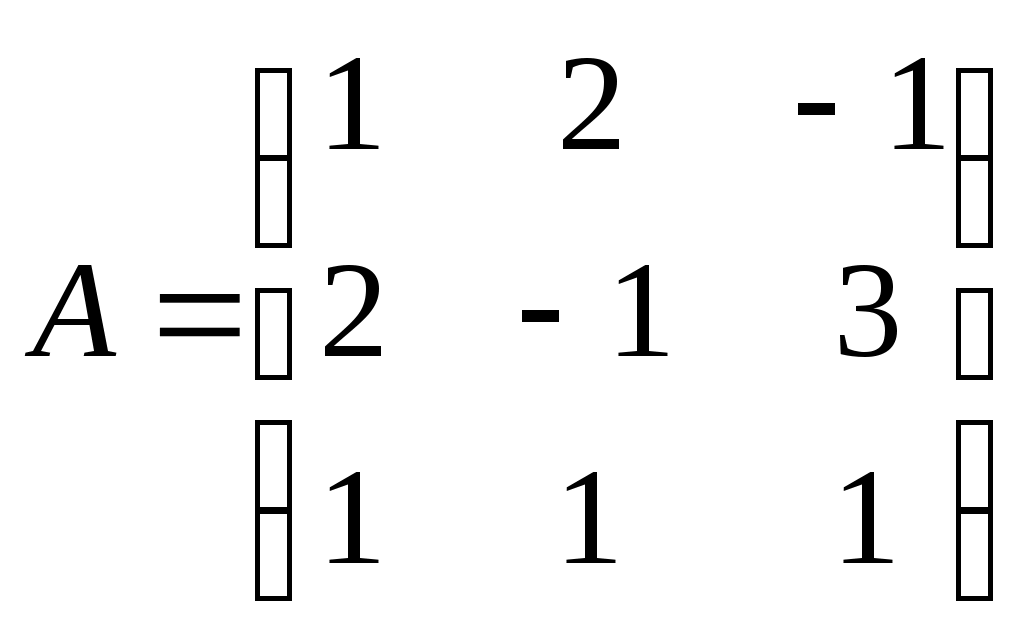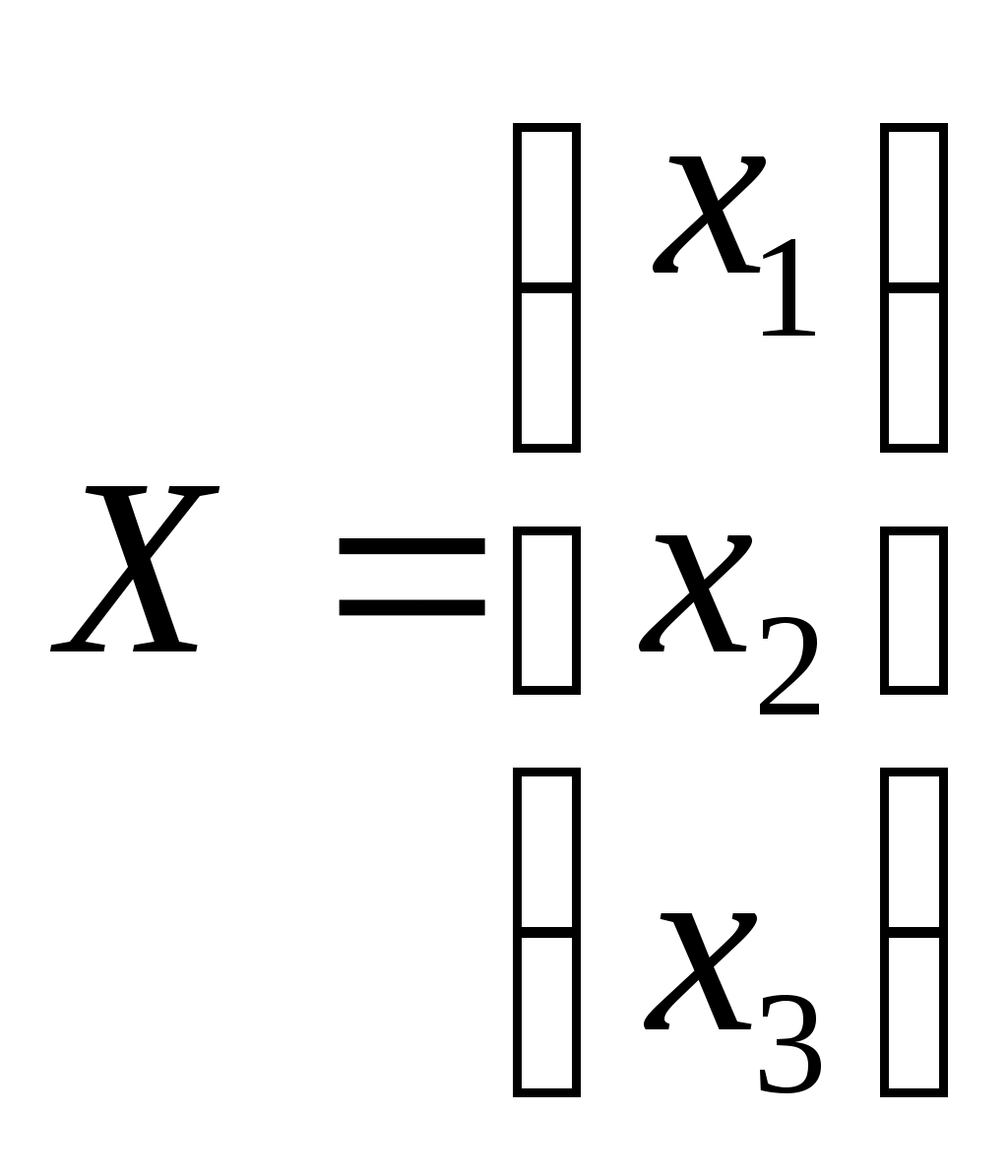
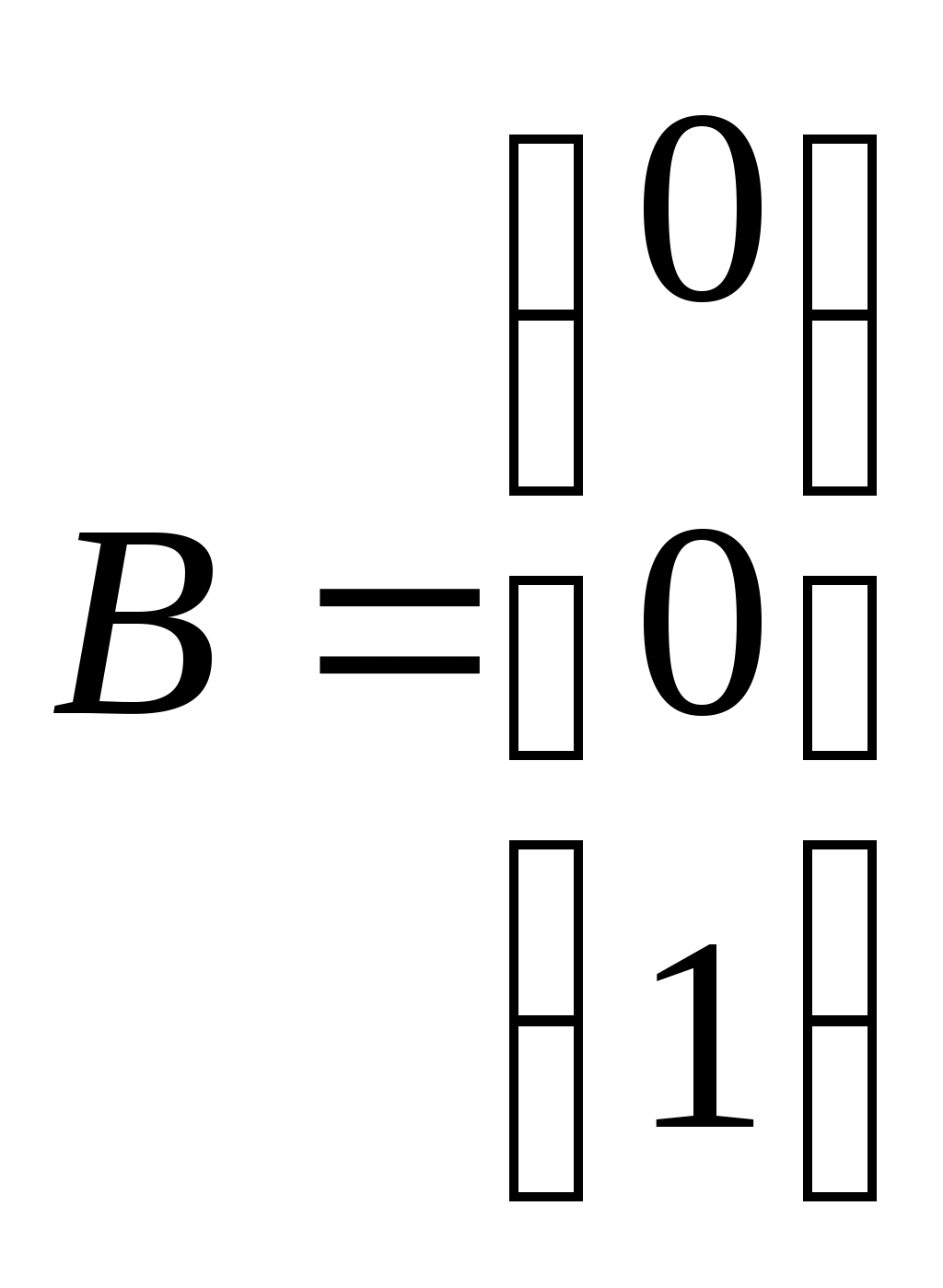Тогда в матричной форме система имеет вид: 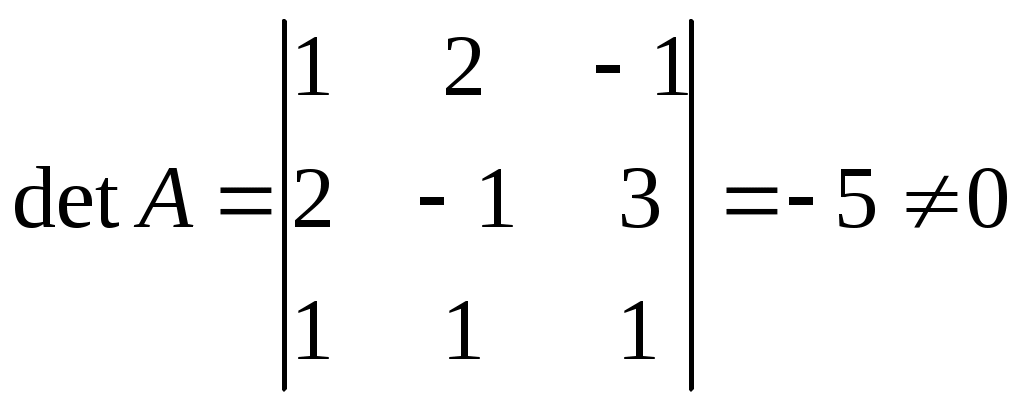. Определитель матрицы , т.е. обратная матрица существует: .

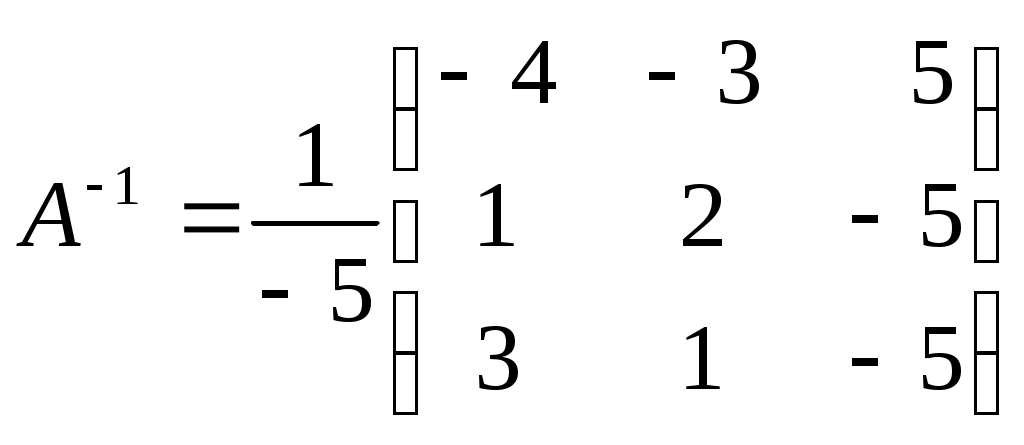Определим ,



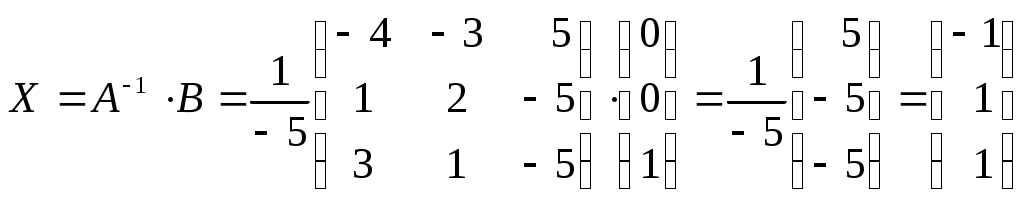Существенным недостатком решения систем линейных уравнений с переменными по формулам Крамера и методом обратной матрицы является их большая трудоемкость, связанная с вычислением определителей и нахождения обратной матрицы.

11. Теорема и формулы Крамера решения системы п линейных уравнений с п переменными (без вывода).

Теорема Крамера. Пусть - определитель матрицы системы, а - определитель матрицы, получаемой из матрицы заменой -го столбца столбцом свободных членов. Тогда, если , то система имеет единственное решение, определяемое по формулам:

, ( ).

В соответствии с обратной матрицей , где - матрица, присоединенная к матрице . Т.к. элементы матрицы есть алгебраические дополнения элементов матрицы , транспонированной к , то запишем равенство в развернутой форме:

.

Учитывая, что , получим после умножения матриц:

, откуда следует, что для любого .

На основании свойства 9 определителей , где - определитель матрицы, полученной из матрицы заменой -го столбца столбцом свободных членов. Следовательно

---

.
Решение системы линейных уравнений с неизвестными

Рассмотрим систему линейных уравнений с неизвестными.

Теорема Кронекера-Капелли. Система линейных уравнений совместна тогда и только тогда, когда ранг матрицы системы равен рангу расширенной матрицы этой системы: .

Для совместных систем линейных уравнений верны следующие теоремы:

Теорема 1. Если ранг матрицы совместной системы равен числу переменных, т.е. , то система имеет единственное решение.

Теорема 2. Если ранг матрицы совместной системы меньше числа переменных, т.е. , то система является неопределенной и имеет бесконечное множество решений.

Определение. Базисным минором матрицы называется любой ненулевой минор, порядок которого равен рангу матрицы.

Определение. Те неизвестных, коэффициенты при которых входят в запись базисного минора, называются базисными (или основными), остальные неизвестных называются свободными (или неосновными).

Решить систему уравнений в случае - это значит выразить базисные переменные через свободные. При этом имеем общее решение системы уравнений. Если все свободные переменные равны нулю, то решение системы называется базисным.

Пример. Решить систему методом Гаусса:

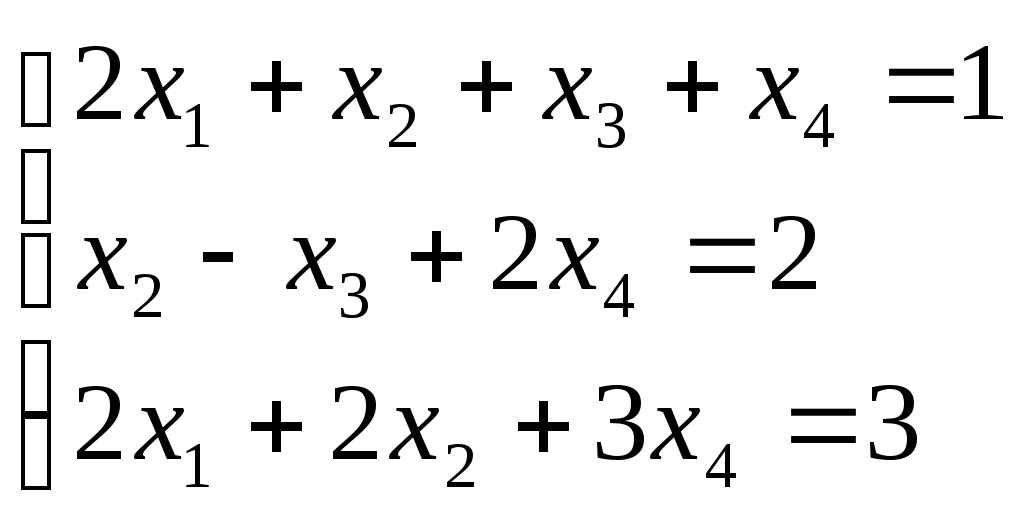
Р е ш е н и е. Выпишем и преобразуем расширенную матрицу системы. Сначала прибавим к элементам третьей строки элементы первой строки, умноженные на –1. А затем элементы второй строки умножим на –1 и прибавим к элементам третьей строки:

---

.

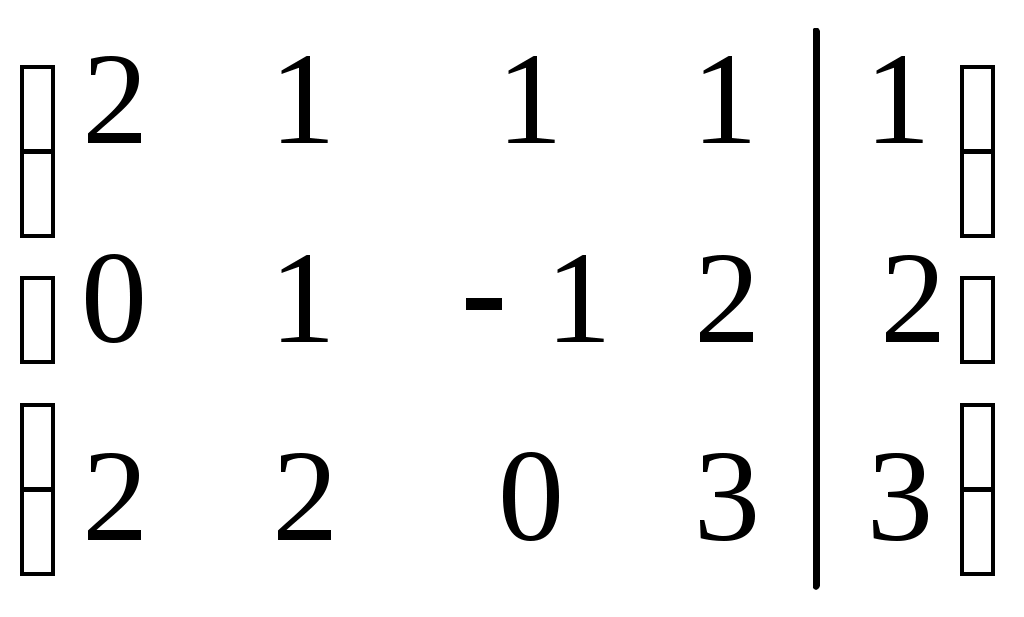
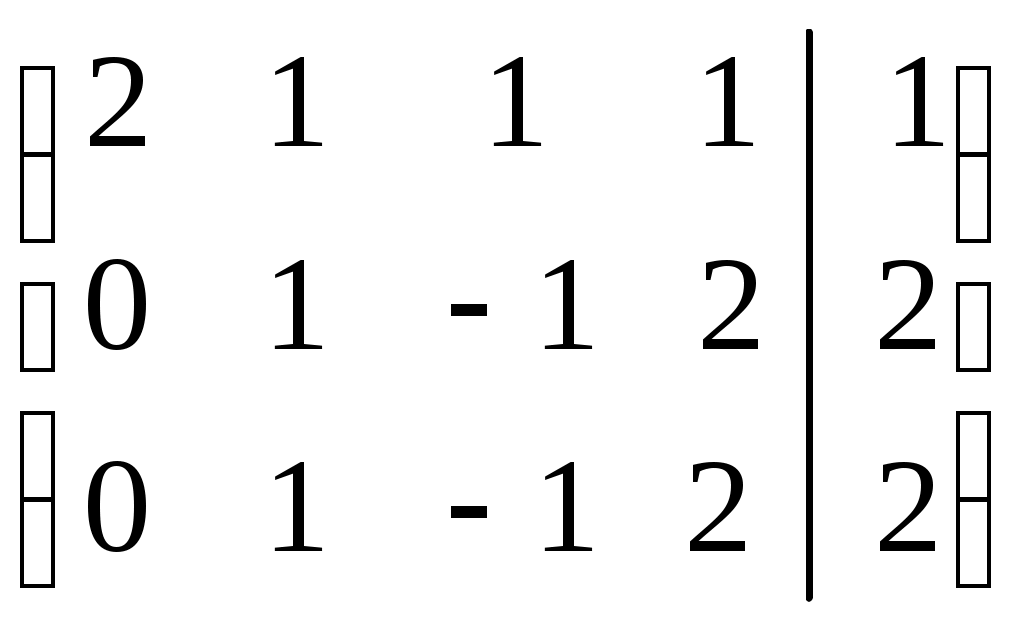
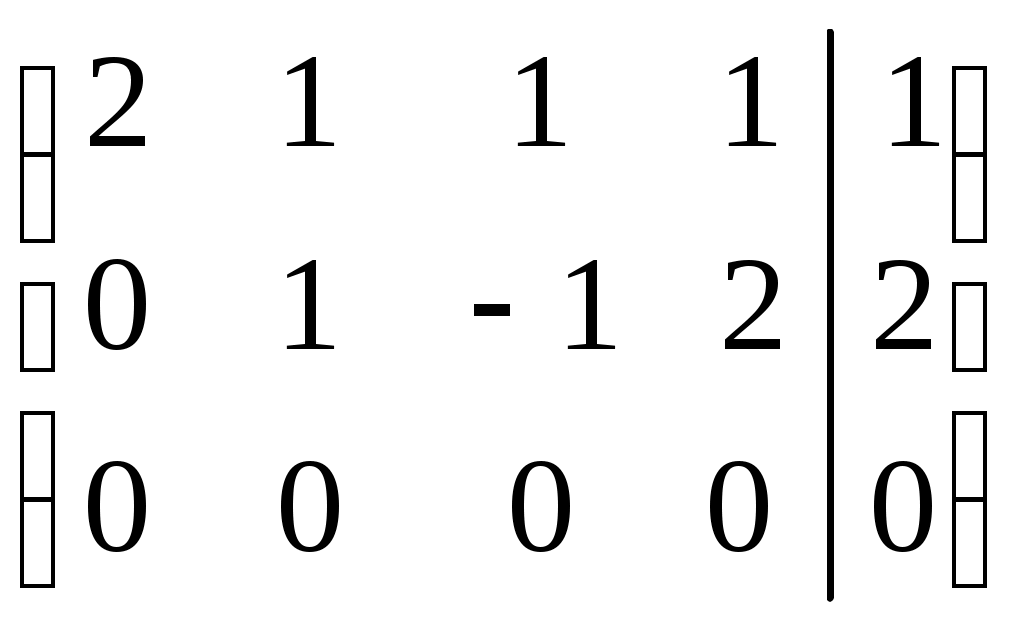Расширенная матрица приведена к ступенчатому виду.

. Так как ранг матрицы равен 2, а количество неизвестных равно 4, то система имеет бесконечное множество решений. В качестве базисных неизвестных возьмем и (т.к. определитель, составленный из их коэффициентов не равен нулю ), тогда и - свободные неизвестные.

Выразим базисные переменные через свободные.

Из второй строки полученной матрицы выразим переменную :

, .

Из первой строки выразим : ,

.

Общее решение системы уравнений: , .

12. Понятие функции, способы задания функций. Область определения. Четные и нечетные, ограниченные, монотонные функции. Примеры.

Понятие функции одной переменной

Постоянной величиной называется величина, сохраняющая одно и то же значение. Например, отношение длины окружности к ее диаметру есть постоянная величина, равная числу .

Если величина сохраняет постоянное значение лишь в условиях данного процесса, она называется параметром

---