Файл: Ответы к экзаменационным вопросам по предмету Основы энергетики.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 02.05.2024
Просмотров: 71
Скачиваний: 0
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Тепловой поток определяется по формуле
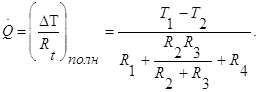(1.7)Отдельные термические сопротивления выражаются соотношением
. 
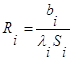Промежуточные температуры типа ТX можно найти из уравнения (1.6).
Предполагается, что при параллельном соединении термических сопротивлений R2 и R3 тепловой поток остается одномерным; если же сопротивления R2 и R3 заметно отличаются друг от друга, могут стать существенными двумерные эффекты.
9. Теплопроводность цилиндрической стенки
Граничные условия первого рода. Рассмотрим стационарный процесс теплопроводности в цилиндрической стенке (трубе) с внутренним диаметром d1=2r1 и наружным диаметром d2=2r2 (рис.2.6). На поверхностях стенки заданы постоянные температуры tc1 и tc2. В заданном интервале температур коэффициент теплопроводности материала стенки λ является постоянной величиной. Необходимо найти распределение температур в цилиндрической стенке и тепловой поток через нее.
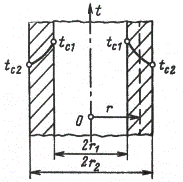
Рис. 2.6. Теплопроводность цилиндрической стенки.
В рассматриваемом случае дифференциальное уравнение теплопроводности удобно записать в цилиндрической системе координат:
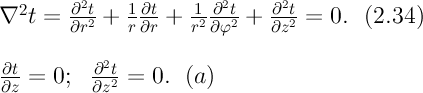Кроме того, так как температуры на наружной и внутренней поверхностях трубы неизменны, изотермические поверхности являются цилиндрическими, имеющими с трубой общую ось. Тогда температура не должна изменяться также вдоль φ, т. е.
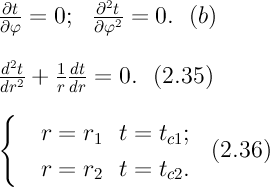В виде (2.35) можно записать уравнение (2.34) с учётом (a) и (b). (2.36) - граничные условия для (2.35). Если решить уравнение (2.35) совместно с (2.36), получим уравнение температурного поля в цилиндрической стенке. Введем новую переменную 
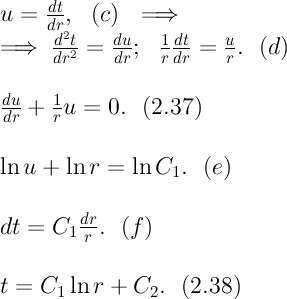Выражение (2.37) получается, если в уравнение (2.35) подставить выражения (
c) и (d). Проинтегрировав (2.37), получаем выражение (е). Потенцируя выражения (е) и переходя к первоначальным переменным, получаем (f). Выражение (2.38) получается в результате интегрирования (f). Постоянные С1 и С2можно определить, если в уравнение (2.38) подставить граничные условия:
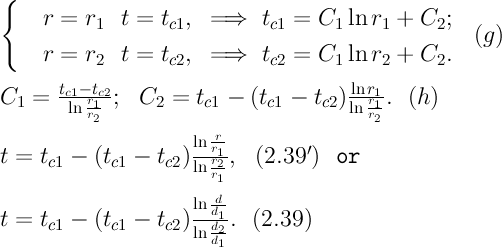Решение уравнений (g) относительноС1 и С2 дает (h). Подставив (h) (значения С1 и С2 ) в уравнение (2.38), получим (2.39') или (2.39). Полученное выражение представляет собой уравнение логарифмической кривой. То обстоятельство, что распределение температуры в цилиндрической стенке является криволинейным, можно объяснить следующим. Для плоской стенки плотность теплового потока qостается одинаковой для всех изотермических поверхностей. По этой причине градиент температуры сохраняет для всех изотермических поверхностей постоянное значение. Для цилиндрической стенки плотность теплового потока через любую изотермическую поверхность зависит от радиуса. Для нахождения количества теплоты, проходящего через цилиндрическую поверхность площадью F в единицу времени, можно воспользоваться законом Фурье: 
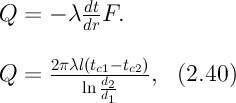Подставляя в уравнение закона Фурье значение градиента температуры согласно уравнению (f), получаем (учитывая, что F=2
rl ) выражение (2.40), где Q измеряется в ваттах. Из уравнения (2.40) следует, что количество теплоты, проходящее через цилиндрическую стенку в единицу времени, полностью определяется заданными граничными условиями и не зависит от радиуса. Тепловой поток (2.40) может быть отнесен либо к единице длины трубы, либо к единице внутренней или внешней поверхности. При этом расчетные формулы для плотности теплового потока, Вт/м2, принимают вид: 
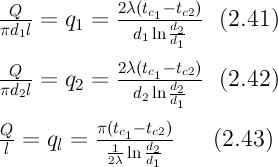(2.41) - тепловой поток через единицу внутренней поверхности; (2.42) - тепловой поток через единицу наружной поверхности; (2.43) - поток теплоты, проходящий через единицу длины трубы, Вт/м. Тепловой поток, отнесенный к единице длины трубы, измеряется в Вт/м и называется линейной плотностью теплового потока. Как видно из уравнения (2.43), при неизменном отношении линейная плотность теплового потока не зависит от поверхности цилиндрической стенки. Плотности теплового потока
q1и q2 (отнесенные к внутренней и внешней поверхности) при передаче теплоты через трубы неодинаковы, причем всегда q1>q2. Последнее ясно видно из уравнений (2.41) и (2.42). Из уравнений (2.41)—(2.43) легко установить связь между величинами q1, q2 и ql:
Когда коэффициент теплопроводности является функцией температуры вида λ(t)=λ0(1+bt), можно показать, что линейную плотность теплового потока можно вычислить по той же формуле, что и для λ=const: 
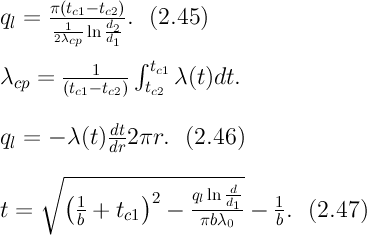λcp – среднеинтегральное значение коэффициента теплопроводности. Для нахождения температурного поля при λ=λ(t)=λ0(1+bt) можно воспользоваться уравнением закона Фурье, записанного для цилиндрической стенки - выражение (2.46). Если разделить переменные и проинтегрировать уравнение (2.46) в пределах от r=r1до r и от t=tc1 до t и найти из полученного интеграла t, то получим выражение для температурного поля - выражение (2.47).Граничные условия третьего рода (теплопередача). Рассмотрим однородную цилиндрическую стенку (трубу) с постоянным коэффициентом теплопроводности λ. Заданы постоянные температуры подвижных сред tF1 и tF2 и постоянные значения коэффициентов теплоотдачи на внутренней и наружной поверхностях трубы
1 и 2 (рис. 2.7).
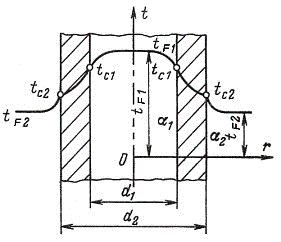
Рис. 2.7. Теплопередача через однородную цилиндрическую стенку.
Необходимо найти ql и tc. Будем полагать, что длина трубы велика по сравнению с толщиной стенки. Тогда потерями теплоты с торцов трубы можно пренебречь, и при установившемся тепловом режиме будет проходить через стенку и отдаваться от стенки к холодной жидкости одно и то же количество теплоты. Следовательно, можно написать:
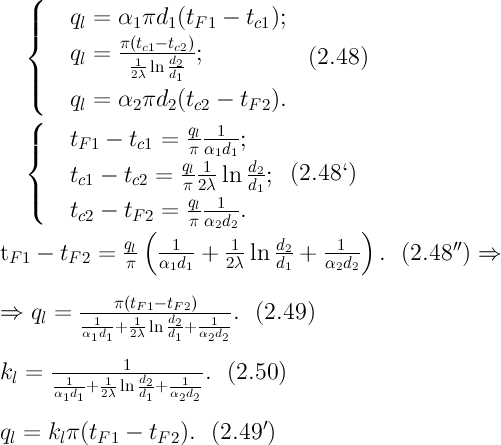
Выражение (2.49) получается из (2.48''). Температурный напор (2.48'') находим в результате сложения уравнений системы (2.48'). Выражения (2.48') получены из (2.48). Величинаkl называется линейным коэффициентом теплопередачи и измеряется в Вт/(м×К). Она характеризует интенсивность передачи теплоты от одной среды к другой через разделяющую их стенку. Значение kl численно равно количеству теплоты, которое проходит через стенку длиной 1м в единицу времени от одной среды к другой при разности температур между ними 1К. Величина Rl=1/kl ,м×К/Вт, обратная линейному коэффициенту теплопередачи, называется линейным термическим сопротивлением теплопередачи. Она равна:
где 1/
1d1 и 1/ 2d2— термические сопротивления теплоотдачи на соответствующих поверхностях, обозначим их соответственно Rl1 и Rl2; 
— термическое сопротивление теплопроводности стенки, обозначим его черезRlc. Следует отметить, что линейные термические сопротивления теплоотдачи для трубы определяются не только коэффициентами теплоотдачи 1и 2, но и соответствующими диаметрами. Если тепловой поток через цилиндрическую стенку отнести к внутренней или наружной поверхности стенки, то получим плотность теплового потока, Вт/м2, отнесенную к единице соответствующей поверхности трубы: 
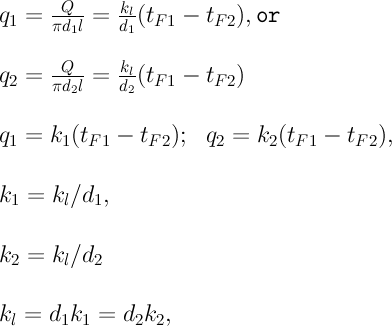гдеklизмеряется в Вт/(м×К). Последнее соотношение устанавливает связь между коэффициентом теплопередачи при отнесении теплового потока к единице длины цилиндрической стенки и к единице поверхности. Формулы же для k1 и k2,Вт/(м
2×К), в развернутом виде имеют вид:
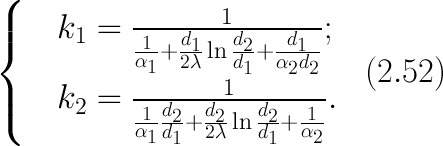На практике часто встречаются цилиндры, толщина стенок которых мала по сравнению с диаметром. В этом случае при расчетах можно пользоваться упрощенными формулами. Для получения таких формул поступим следующим образом. Величину
разложим в ряд:
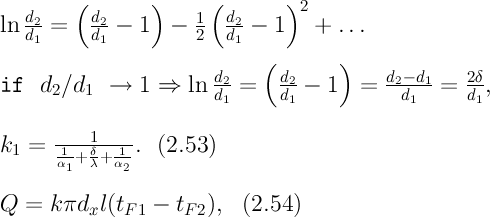Если отношениеd2/d1→1, то такой ряд быстро сходится, и с достаточной точностью можно ограничиться первым членом ряда (где δ - толщина цилиндрической стенки, м). Подставив, полученное значение в уравнение (2.52), получим (2.53). Следовательно, если стенка трубы тонкая, то при практических расчетах можно пользоваться формулой (2.54), гдеk,Вт/(м2×К), взято согласно формуле (2.53), т. е. как для плоской стенки. При этом, если d2/d1<2, погрешность расчета не превышает 4%. Для многих технических расчетов погрешность, не превышающая 4%, вполне допустима. Обычно в инженерных расчетах при d2/d1≤1,8 пользуются формулой (2.54). Погрешность можно уменьшить, если в качестве расчетной поверхности в (2.54) брать поверхность, со стороны которой меньше: 1) если 1>> 2, то dx=d2; 2) если 2>> 1, то dx=d1; 3) если 1≈ 2, то dx=(d1+d2