Файл: Лекция Принципы управления 2 Общие понятия 2 Лекция Статический режим сау 7.doc

, расширяющие его возможности.



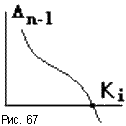
Недостаток критерия Гурвица - малая наглядность. Достоинство - удобен для реализации на ЭВМ. Его часто используют  для  определения  влияния одного из параметров САУ на ее устойчивость. Так равенство нулю главного определителя _n = a_{n n-1} = 0 говорит о том, что система находится на границе устойчивости. При этом либо a_n = 0 - при выполнении остальных условий система находится на границе апериодической устойчивости, либо предпоследний минор _n-1 = 0 - при положительности всех остальных миноров система находится на границе колебательной устойчивости. Параметры САУ определяют значения коэффициентов уравнения динамики, следовательно изменение любого параметра Ki влияет на значение определителя _n-1. Исследуя это влияние можно найти, при каком значении Ki определитель _n-1 станет равен нулю, а потом - отрицательным (рис.67). Это и будет предельное значение исследуемого параметра, после которого система становится неустойчивой.

---

Лекция 9. Частотные критерии устойчивости

Это графоаналитические методы, позволяющие по виду частотных характеристик САУ судить об их устойчивости. Их общее достоинство в простой геометрической интерпретации, наглядности и в отсутствии ограничений на порядок дифференциального уравнения.

 

9.1. Принцип аргумента

 

Запишем характеристический полином САУ в виде

 

D(p) = a₀ (p - p₁) (p - p₂) ... (p - p_n) = 0.

 

 



 

 

Его корни

p_i = _i + j i = |p_i|e^jarg(pi),

 

где arg(p_i) = arctg( i/a_i) + k ,

.

 

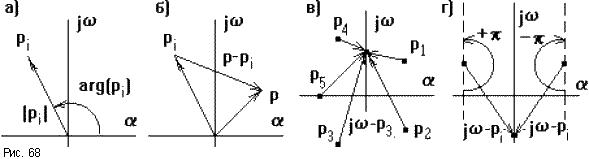
Каждый корень можно изобразить вектором на комплексной плоскости (рис.68а), тогда разность p - p_i изобразится разностью векторов (рис.68б), где p - любое число.

Еcли менять значение p произвольным образом, то конец вектора p - p_i будет перемещаться по комплексно плоскости, а его начало будет оставаться неподвижным, так как p_i - это конкретное неизменное значение.

В частном случае, если на вход системы подавать гармонические колебания с различной частотой , то p = j , а характеристический полином принимает вид:

D(j ) = a₀ (j - p₁) (j - p₂) ... (j - p_n).

 

При этом концы векторов j - p_i будут находиться на мнимой оси (рис.68в). Если менять от - до + , то каждый вектор j - p_i будет поворачиваться относительно своего начала p_i на угол +p для левых и - p для правых корней (рис.68г).

Характеристический полином можно представить в виде

 

D(j ) = |D(j )|e^{jarg(D(j )}),

где    |D(j )| = a₀ |j - p₁| |j - p₂

---

|...|j - p_n|,

arg(D(j )) = arg(j - p₁) + arg(j - p₂) + .. + arg(j - p_n).

 

Пусть из n корней m - правые, а n - m - левые, тогда угол поворота вектора D(j ) при изменении от - до + равен

 

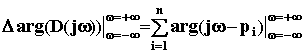= (n - m) - m ,

 

или при изменении от 0 до + получаем

= (n - 2m) ( /2).

 

Отсюда вытекает правило: изменение аргумента вектора b при изменении частоты от - до + равно разности между числом левых и правых корней уравнения D(p) = 0, умноженному на , а при изменении частоты от 0 до + эта разность умножается на /2.

Это и есть принцип аргумента. Он положен в основе всех частотных критериев устойчивости. Мы рассмотрим два наиболее распространенных критерия: критерий Михайлова и критерий Найквиста.

 

9.2. Критерий устойчивости Михайлова

 

Так как для устойчивой САУ число правых корней m = 0, то угол поворота вектора D(j ) составит

 

= n /2.

 

То есть САУ будет устойчива, если вектор D(j ) при изменении частоты от 0 до + повернется на угол n /2.



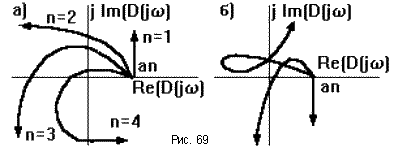
При этом конец вектора опишет кривую, называемую годографом Михайлова. Она начинается на положительной полуоси, так как D(0) = a_n, и последовательно проходит против часовой стрелки n квадрантов комплексной плоскости, уход в бесконечность в n - ом квадранте  (рис.69а).

Если это правило нарушается (например, число проходимых кривой квадрантов не равно n, или нарушается последовательность прохождения квадрантов  (рис.69б)), то такая САУ неустойчива - это и есть необходимое и достаточное условие критерия Михайлова.

Достоинства. Этот критерий удобен своей наглядностью. Так, если кривая проходит вблизи начала координат, то САУ находится вблизи границы устойчивости и наоборот. Этим критерием удобно пользоваться, если известно уравнение замкнутой САУ.

Для облегчения построения годографа Михайлова выражение для

---

D(j ) представляют суммой вещественной и мнимой составляющих:

 

 D(j ) = a₀(j - p₁)(j - p₂)...(j - p_n) = a₀(j )ⁿ + a₁(j )^{n - 1} + ... + a_n = ReD(j ) + jImD(j ),

где

ReD(j ) = a_n - a_{n - 2} ² + a_{n- 4} ⁴ - ...,

ImD(j ) = a_{n - 1} - a_{n - 3} ³ + a_{n- 5} ⁵ - ....

 

Меняя от 0 до по этим формулам находят координаты точек годографа, которые соединяют плавной линией.

 

---

9.3. Критерий устойчивости Найквиста

Этот критерий позволяет судить об устойчивости замкнутой САУ по виду АФЧХ разомкнутой САУ (рис.70). Исследование разомкнутой САУ проще, чем замкнутой. Его можно производить экспериментально, поэтому часто оказывается, что АФЧХ разомкнутой САУ мы имеем или можем получить.

Передаточная функция разомкнутой САУ:

 

W_p(p) = W_p(p)/D_p(p) = > уравнение динамики: y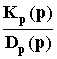(t) = e(t),

 

или

D_p(p) y(t) = K_p(p) e(t).

 

Здесь D_p(p) - характеристический полином разомкнутой САУ. То есть по виду корней уравнения D_p(p) = 0 можно судить об устойчивости разомкнутой САУ. Но это пока ничего не говорит об устойчивости замкнутой САУ.

Для того, чтобы получить уравнение динамики замкнутой САУ при свободном движении, считаем, что внешнее воздействие u = 0, тогда на вход первого звена САУ подается сигнал

 

e(t) = u(t) - y(t) = - y(t).

 

То есть

 

D_p(p) y(t) = K_p(p) ( - y(t)),

 

следовательно уравнение замкнутой САУ:

 

(D_p(p) + K_p(p)) y(t) = 0.

Таким образом, характеристическое уравнение замкнутой САУ:

 

D_з(p) = D_p(p) + K_p(p) = 0.

 

По виду его корней уже можно судить об устойчивости замкнутой САУ.

Воспользуемся вспомогательной функцией:

 

F(j ) = 1 + W_р(j ) = .

 

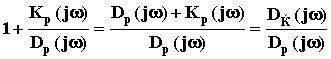По сути дела она представляет собой АФЧХ разомкнутой САУ, сдвинутую на единицу вправо. Степени полиномов D_з(j ) и D_p(j ) равны n. Эти полиномы имеют свои корни p_зi и p_pi, то есть можно записать:

 

F(jw) = .

 

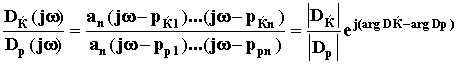Каждую разность в скобках можно представить вектором на комплексной плоскости, конец которого скользит по мнимой оси (рис.63в). При изменении от - до + каждый из векторов

---