ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 03.05.2024
Просмотров: 190
Скачиваний: 0
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
N, после чего отбираются каждые N/n-е объекты для выборки, находящиеся на равном расстоянии друг от друга (n – объем выборки, N – объем генеральной совокупности).
Величина N/n называется шагом, или интервалом отбора между выбираемыми элементами. Например, если для 1000 единиц требуется создать 5-процентную выборочную совокупность, то объем выборки будет 50 единиц, интервал отбора составит 1000 / 50 = 20. Это значит, что в выборку попадет каждый 20-й элемент генеральной совокупности.
Существуют два способа формирования основы механической выборки: по неранжированным (по отношению к изучаемым признакам) данным и по ранжированной генеральной совокупности.
В первом случае результаты механического отбора будут являться реализацией случайного бесповторного отбора, так как единицы наблюдения располагаются в случайном порядке. Усилить данную случайность возможно выбором начальной точки отсчета случайным образом из интервала, соответствующего первому шагу отбора.
Во втором случае единицы наблюдения определенным образом упорядочиваются по величине изучаемого признака и отбор осуществляется в соответствии с его шагом N/n, начиная с единицы, являющейся серединой первого интервала.
Однако метод систематического отбора имеет серьезные недостатки из-за невозможности оценить точность получаемой выборки. Недопустимо использование систематической выборки в случае повторяемости некоторого ее фрагмента, который по размеру соответствует и интервалу отбора. Например, если во время упаковки на конвейере каждому 20-му изделию уделяют особое внимание и по воле случая при шаге выборки № 20 вы отберете в свою систематическую выборку именно эти изделия, то результаты систематической выборки будут полностью бесполезны в отношении репрезентативности качества других обычных изделий.
Стратифицированную случайную выборку применяют, когда генеральная совокупность содержит ясные, известные, легко идентифицированные группы. Такие группы также называются слоями (стратами), в связи с чем типический отбор называют также стратифицированным, или расслоенным. При обследованиях населения в качестве типических групп могут быть выбраны области, районы, социальные, возрастные или образовательные группы, при обследовании предприятий – отрасли или подотрасли, формы собственности и т.п.
Стратифицированную выборку получают путем осуществления случайной выборки отдельно в каждой страте генеральной совокупности. Существуют следующие два вида организации отбора внутри типической группы:
· пропорционально объему типических групп;
· пропорционально степени колеблемости значений признака у единиц наблюдения в группах.
При проведении отбора пропорционально объему типических групп число единиц, подлежащих отбору из каждой группы, определяется следующим образом:
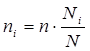, (58)
где
ni – количество извлекаемых единиц для выборки из i-й типической группы;
n – общий объем выборки;
Ni – количество единиц генеральной совокупности, составивших i-ю типическую группу;
N – общее количество единиц генеральной совокупности.
Размеры выборки для каждой из страт могут быть разными. Для одних страт процесс отбора может быть сложнее и дороже, чем для других, и для этих страт используются меньшие по размеру выборки. Другие страты могут иметь большую изменчивость, и поэтому для них требуется использовать большие по размеру выборки. Рассматривать генеральную совокупность в разрезе нескольких крупных групп единиц имеет смысл только в том случае, если средние значения изучаемых признаков по группам существенно различаются. В то же время, нет никакого смысла при выделении типических групп ориентироваться на признак, не связанный или очень слабо связанный с изучаемым.
Вопрос 3. Средняя и предельная ошибка выборки. Построение доверительных границ для среднего и доли.
Из одной и той же генеральной совокупности объемом N единиц можно извлечь множество различных выборок заданного объема n. Тогда в каждом случае рассчитанные отклонения выборочных характеристик от генеральных будут различны. Если определить среднюю из ошибок всех возможных выборок заданного объема, то получим их обобщающую характеристику – среднюю ошибку выборки (μ), которая показывает, насколько отклоняется в среднем параметр выборочной совокупности от соответствующего параметра генеральной.
Ошибка выборки, или отклонение выборочной средней от средней генеральной, находится в прямой зависимости от дисперсии изучаемого признака в генеральной совокупности и в обратной зависимости – от объема выборки. Таким образом, среднюю ошибку выборки можно представить как
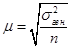
(59)
При проведении выборочного наблюдения дисперсия изучаемого признака в генеральной совокупности, как правило, не известна. В то же время между генеральной дисперсией и средней из всех возможных выборочных дисперсий существует следующая зависимость:
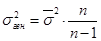(60)
В связи с тем, что на практике в большинстве случаев из генеральной совокупности в определенный момент времени производится только одна выборка, дисперсия изучаемого признака по этой выборке и используется при расчете ошибки. При достаточно большом объеме выборки отношение близко к 1.
При бесповторном отборе необходимо учитывать поправку на конечность совокупности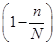
.
При стратифицированной выборке в выборочную совокупность в той или иной пропорции обязательно попадают представители всех групп, поэтому при типизации генеральной совокупности исключается влияние межгрупповой дисперсии на среднюю ошибку выборки. В то же время в выделенных типических группах обследуются далеко не все единицы, а только включенные в выборку. Следовательно, на величине полученной ошибки будет сказываться различие между единицами внутри этих групп, т.е. внутригрупповая вариация. Поэтому ошибка типической выборки будет определяться величиной не общей дисперсии, а только ее части – средней из внутригрупповых дисперсий.
Формулы для определения средней ошибки выборки индивидуальны для различных способов отбора (повторного и бесповторного), видов используемых выборок и оцениваемых статистических показателей (таблица 37).
Таблица 37.
Формулы для расчета средней ошибки выборки (μ)
Для определения возможных границ значений характеристик генеральной совокупности рассчитывается предельная ошибка выборки (Δ), которая зависит от величины ее средней ошибки и уровня вероятности, с которым гарантируется, что генеральная средняя не выйдет за указанные границы:
(61)
Уровень предельной ошибки выборки зависит от следующих факторов:
· от степени вариации единиц генеральной совокупности;
· от объема выборки;
· от выбранных схем отбора – повторного и бесповторного;
· от уровня доверительной вероятности.
Согласно теореме А.М. Ляпунова, вероятность той или иной величины предельной ошибки при достаточно большом объеме выборочной совокупности подчиняется нормальному закону распределения и может быть определена на основе интеграла Лапласа.
Значения интеграла Лапласа при различных величинах t табулированы и представлены в статистических справочниках. Если объем выборки больше 30, то значение t определяется по таблице нормального распределения, если меньше – по таблице распределения Стьюдента. При обобщении результатов выборочного наблюдения наиболее часто используются следующие уровни вероятности и соответствующие им значения t:
Например, если при расчете предельной ошибки выборки мы используем значение t = 2, то с вероятностью 0,954 можно утверждать, что расхождение между выборочной средней и генеральной средней не превысит двукратной величины средней ошибки выборки.
Построение доверительных интервалов для генеральной средней и доли осуществляется следующим образом:
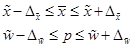(62)
Определение границ генеральной средней и доли состоит из следующих этапов:
· нахождение выборочного значения средней (или доли);
· определение средней ошибки выборки в соответствии с выбранной схемой отбора и видом выборки;
· задание доверительной вероятности Р и определение коэффициента доверия t;
· вычисление предельной ошибки выборки ;
· построение доверительного интервала для среднего (доли).
Пример 1. Для изучения среднего размера расходов на стоматологическую страховку, которую готовы заплатить служащие банка в год, из 1350 банковских работников было обследовано 810 человек методом случайного повторного отбора. В результате были получены следующие данные (таблица 38).
Таблица 38.
Результаты выборочного обследования банковских служащих на предмет размера расходов на стоматологическую страховку
Определите с вероятностью 0,954:
а) предельную ошибку выборки и границы для генеральной средней;
б) в каких границах находится генеральная доля банковских служащих, готовых израсходовать на страховку не более 1000 долл.
Решение:
1. По результатам выборочного обследования рассчитаем среднее значение и дисперсию выборочной совокупности, для чего необходимо рассчитать середины интервалов группировочного признака «размер расходов» (табл. 38). Для удобства расчетов построим вспомогательную таблицу 39.
Таблица 39.
Вспомогательная таблица для расчета среднего размера страховки и дисперсии
Величина N/n называется шагом, или интервалом отбора между выбираемыми элементами. Например, если для 1000 единиц требуется создать 5-процентную выборочную совокупность, то объем выборки будет 50 единиц, интервал отбора составит 1000 / 50 = 20. Это значит, что в выборку попадет каждый 20-й элемент генеральной совокупности.
Существуют два способа формирования основы механической выборки: по неранжированным (по отношению к изучаемым признакам) данным и по ранжированной генеральной совокупности.
В первом случае результаты механического отбора будут являться реализацией случайного бесповторного отбора, так как единицы наблюдения располагаются в случайном порядке. Усилить данную случайность возможно выбором начальной точки отсчета случайным образом из интервала, соответствующего первому шагу отбора.
Во втором случае единицы наблюдения определенным образом упорядочиваются по величине изучаемого признака и отбор осуществляется в соответствии с его шагом N/n, начиная с единицы, являющейся серединой первого интервала.
Однако метод систематического отбора имеет серьезные недостатки из-за невозможности оценить точность получаемой выборки. Недопустимо использование систематической выборки в случае повторяемости некоторого ее фрагмента, который по размеру соответствует и интервалу отбора. Например, если во время упаковки на конвейере каждому 20-му изделию уделяют особое внимание и по воле случая при шаге выборки № 20 вы отберете в свою систематическую выборку именно эти изделия, то результаты систематической выборки будут полностью бесполезны в отношении репрезентативности качества других обычных изделий.
Стратифицированную случайную выборку применяют, когда генеральная совокупность содержит ясные, известные, легко идентифицированные группы. Такие группы также называются слоями (стратами), в связи с чем типический отбор называют также стратифицированным, или расслоенным. При обследованиях населения в качестве типических групп могут быть выбраны области, районы, социальные, возрастные или образовательные группы, при обследовании предприятий – отрасли или подотрасли, формы собственности и т.п.
Стратифицированную выборку получают путем осуществления случайной выборки отдельно в каждой страте генеральной совокупности. Существуют следующие два вида организации отбора внутри типической группы:
· пропорционально объему типических групп;
· пропорционально степени колеблемости значений признака у единиц наблюдения в группах.
При проведении отбора пропорционально объему типических групп число единиц, подлежащих отбору из каждой группы, определяется следующим образом:
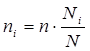, (58)где
ni – количество извлекаемых единиц для выборки из i-й типической группы;
n – общий объем выборки;
Ni – количество единиц генеральной совокупности, составивших i-ю типическую группу;
N – общее количество единиц генеральной совокупности.
Размеры выборки для каждой из страт могут быть разными. Для одних страт процесс отбора может быть сложнее и дороже, чем для других, и для этих страт используются меньшие по размеру выборки. Другие страты могут иметь большую изменчивость, и поэтому для них требуется использовать большие по размеру выборки. Рассматривать генеральную совокупность в разрезе нескольких крупных групп единиц имеет смысл только в том случае, если средние значения изучаемых признаков по группам существенно различаются. В то же время, нет никакого смысла при выделении типических групп ориентироваться на признак, не связанный или очень слабо связанный с изучаемым.
Вопрос 3. Средняя и предельная ошибка выборки. Построение доверительных границ для среднего и доли.
Из одной и той же генеральной совокупности объемом N единиц можно извлечь множество различных выборок заданного объема n. Тогда в каждом случае рассчитанные отклонения выборочных характеристик от генеральных будут различны. Если определить среднюю из ошибок всех возможных выборок заданного объема, то получим их обобщающую характеристику – среднюю ошибку выборки (μ), которая показывает, насколько отклоняется в среднем параметр выборочной совокупности от соответствующего параметра генеральной.
Ошибка выборки, или отклонение выборочной средней от средней генеральной, находится в прямой зависимости от дисперсии изучаемого признака в генеральной совокупности и в обратной зависимости – от объема выборки. Таким образом, среднюю ошибку выборки можно представить как
(59)
При проведении выборочного наблюдения дисперсия изучаемого признака в генеральной совокупности, как правило, не известна. В то же время между генеральной дисперсией и средней из всех возможных выборочных дисперсий существует следующая зависимость:
(60)В связи с тем, что на практике в большинстве случаев из генеральной совокупности в определенный момент времени производится только одна выборка, дисперсия изучаемого признака по этой выборке и используется при расчете ошибки. При достаточно большом объеме выборки отношение близко к 1.
При бесповторном отборе необходимо учитывать поправку на конечность совокупности
.При стратифицированной выборке в выборочную совокупность в той или иной пропорции обязательно попадают представители всех групп, поэтому при типизации генеральной совокупности исключается влияние межгрупповой дисперсии на среднюю ошибку выборки. В то же время в выделенных типических группах обследуются далеко не все единицы, а только включенные в выборку. Следовательно, на величине полученной ошибки будет сказываться различие между единицами внутри этих групп, т.е. внутригрупповая вариация. Поэтому ошибка типической выборки будет определяться величиной не общей дисперсии, а только ее части – средней из внутригрупповых дисперсий.
Формулы для определения средней ошибки выборки индивидуальны для различных способов отбора (повторного и бесповторного), видов используемых выборок и оцениваемых статистических показателей (таблица 37).
Таблица 37.
Формулы для расчета средней ошибки выборки (μ)
| | Способ отбора | |
| повторный | бесповторный | |
| Вид выборки | Собственно случайная выборка | |
| При оценке среднего |  |  |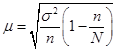
| При оценке доли |  |  |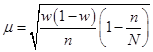
| При оценке суммарного значения признака |  |  |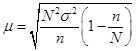
| Вид выборки | Систематическая (механическая) выборка | |
| При оценке среднего | - | |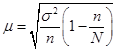
| При оценке доли | - | |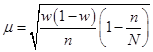
| При оценке суммарного значения признака | - | |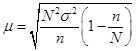
| Вид выборки | Стратифицированная (типическая) выборка | |
| При оценке среднего |  |  |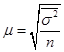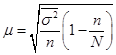
| При оценке доли |  |  |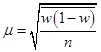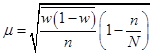
| При оценке суммарного значения признака |  |  |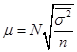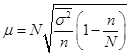
| где w (1 – w) – выборочная дисперсия доли; – среднегрупповая дисперсия типических групп. | ||
Для определения возможных границ значений характеристик генеральной совокупности рассчитывается предельная ошибка выборки (Δ), которая зависит от величины ее средней ошибки и уровня вероятности, с которым гарантируется, что генеральная средняя не выйдет за указанные границы:
(61)
Уровень предельной ошибки выборки зависит от следующих факторов:
· от степени вариации единиц генеральной совокупности;
· от объема выборки;
· от выбранных схем отбора – повторного и бесповторного;
· от уровня доверительной вероятности.
Согласно теореме А.М. Ляпунова, вероятность той или иной величины предельной ошибки при достаточно большом объеме выборочной совокупности подчиняется нормальному закону распределения и может быть определена на основе интеграла Лапласа.
Значения интеграла Лапласа при различных величинах t табулированы и представлены в статистических справочниках. Если объем выборки больше 30, то значение t определяется по таблице нормального распределения, если меньше – по таблице распределения Стьюдента. При обобщении результатов выборочного наблюдения наиболее часто используются следующие уровни вероятности и соответствующие им значения t:
| Значение доверительной вероятности P | 0,6827 | 0,8664 | 0,9545 | 0,9973 |
| Значение коэффициента доверия t | 1,000 | 1,500 | 2,000 | 3,000 |
Например, если при расчете предельной ошибки выборки мы используем значение t = 2, то с вероятностью 0,954 можно утверждать, что расхождение между выборочной средней и генеральной средней не превысит двукратной величины средней ошибки выборки.
Построение доверительных интервалов для генеральной средней и доли осуществляется следующим образом:
(62)Определение границ генеральной средней и доли состоит из следующих этапов:
· нахождение выборочного значения средней (или доли);
· определение средней ошибки выборки в соответствии с выбранной схемой отбора и видом выборки;
· задание доверительной вероятности Р и определение коэффициента доверия t;
· вычисление предельной ошибки выборки ;
· построение доверительного интервала для среднего (доли).
Пример 1. Для изучения среднего размера расходов на стоматологическую страховку, которую готовы заплатить служащие банка в год, из 1350 банковских работников было обследовано 810 человек методом случайного повторного отбора. В результате были получены следующие данные (таблица 38).
Таблица 38.
Результаты выборочного обследования банковских служащих на предмет размера расходов на стоматологическую страховку
| Размер страховки, дол. | до 250 | 250–500 | 500–750 | 750–1000 | 1000–1250 | 1250–1500 | |
| Количество человек | 80 | 105 | 134 | 231 | 169 | 91 | 810 |
Определите с вероятностью 0,954:
а) предельную ошибку выборки и границы для генеральной средней;
б) в каких границах находится генеральная доля банковских служащих, готовых израсходовать на страховку не более 1000 долл.
Решение:
1. По результатам выборочного обследования рассчитаем среднее значение и дисперсию выборочной совокупности, для чего необходимо рассчитать середины интервалов группировочного признака «размер расходов» (табл. 38). Для удобства расчетов построим вспомогательную таблицу 39.
Таблица 39.
Вспомогательная таблица для расчета среднего размера страховки и дисперсии
| Размер страховки, долл. xi | Количество человек fi | Середина интервала, | | |
| до 250 | 80 | 125 | 10 000 | 1 250 000 |
| 250–500 | 105 | 375 | 39 375 | 14 765 625 |
| 500–750 | 134 | 625 | 83 750 | 52 343 750 |
| 750–1000 | 231 | 875 | 202 125 | 176 859 375 |
| 1 000–1 250 | 169 | 1125 | 190 125 | 213 890 625 |
| 1 250–1 500 | 91 | 1375 | 125 125 | 172 046 875 |
| Итого: | 810 | - | 650 500 | 631 156 250 |