ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 03.05.2024
Просмотров: 189
Скачиваний: 0
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Выборочная средняя составит:
Выборочная дисперсия изучаемого признака:
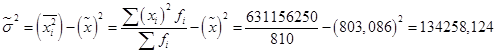
Выборочное среднеквадратическое отклонение составит:
2. Определим среднюю ошибку повторной случайной выборки:
3. Определим предельную ошибку выборки с заданной вероятностью. Для этого по таблице значений вероятности функции нормального распределения находим величину коэффициента доверия t, соответствующего вероятности 0,954. При F(t) = 0,954, t = 2.
Предельная ошибка выборки с вероятностью 0,954 равна:
Найдем доверительные границы для среднего значения размера страховки:
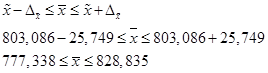
Таким образом, в 954 случаях из 1000 средний объем денежных средств, которые служащие готовы потратить на стоматологическую страховку в год, не будет превышать 828,8 долл. и не будет меньшим, чем 777,3 долл.
Теперь определим, в каких границах в генеральной совокупности находится доля банковских служащих, готовых израсходовать на страховку не более 1000 долл.
4. Рассчитаем выборочную долю. Количество банковских работников, готовых потратить на страховку не более 1000 долл., в выборочной совокупности составляет 550 ед., следовательно: m = 550, n = 810, w = m / n= 550 / 810 = 0,679.
5. Рассчитаем выборочную дисперсию доли:
6. Средняя ошибка выборки при использовании повторной схемы отбора составит:
Предположим, что была использована бесповторная схема отбора. Тогда средняя ошибка выборки с учетом поправки на конечность совокупности составит:
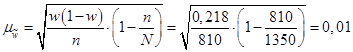
7. Определим предельную ошибку выборки. При значении вероятности р = 0,954 по таблице нормального распределения получаем значение коэффициента доверия t = 2.
8. Определим границы для генеральной доли с вероятностью 95,4 % для бесповторного отбора:
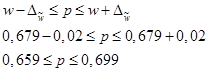
Следовательно, с вероятностью 0,954 можно утверждать, что в генеральной совокупности доля сотрудников, готовых израсходовать на стоматологическую страховку не более 1 000 долл. в год, не меньше 65,9 % и не больше 69,9 %.
Пример 2. Руководстворегионально-распределенной корпорации дало поручение провести исследование частоты обращения сотрудников к недавно введенной в эксплуатацию корпоративной базе знаний, содержащей сведения об истории реализации корпорацией проектов, инструкции по действию и ответы на вопросы о действиях сотрудника в сложных производственных ситуациях, экспресс-курсы повышения квалификации и другую справочную информацию. Для этих целей была использована 15 % бесповторная типическая выборка, типические группы которой соответствуют региональному отделению. При отборе, пропорциональному объему типических групп, получены данные (таблица 40).
Таблица 40.
Результаты обследования сотрудников корпорации
| Региональное отделение | Всего сотрудников, чел. Ni | Обследовано в результате выборочного наблюдения, чел., ni | Среднее число обращений одного сотрудника к корпоративной базе знаний за полгода, | Внутригрупповая выборочная дисперсия, |
| А | 650 | 98 | 11 | 9 |
| Б | 610 | 92 | 8 | 15 |
| В | 580 | 87 | 5 | 18 |
| Г | 360 | 54 | 6 | 24 |
| Д | 350 | 52 | 10 | 12 |
| Итого: | 2550 | 383 | - | - |
Общий объем выборочной совокупности составит:
Количество сотрудников, которое необходимо обследовать в каждом региональном отделении, определим согласно формуле:
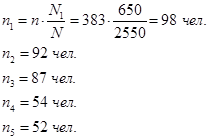
1. Выборочная средняя, основываясь на значениях средних типических групп, составит:
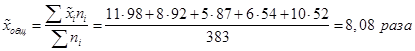
2. Средняя из внутригрупповых дисперсий равна:
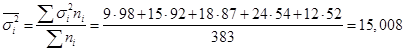
3. Средняя ошибка выборки:
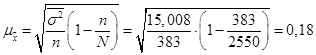
С вероятностью 0,954 находим предельную ошибку выборки:
4. Доверительные границы для среднего находятся в пределах:
Вопрос 4. Определение объема выборочной совокупности.
Важным вопросом, особенно на этапе проектирования выборочного наблюдения, является определение объема выборочной совокупности.
Чем больше объем выборки, тем меньше значения средней и предельной ошибок выборочного наблюдения и, следовательно, тем уже границы генеральной средней и генеральной доли. В то же время необходимо учитывать, что большой объем выборки приводит к удорожанию обследования, увеличению сроков сбора и обработки материалов, требует привлечения дополнительного персонала и соответствующего материально-технического обеспечения. Затраты всех ресурсов на 20–30 %-ное выборочное наблюдение уже сопоставимы с расходами на сплошное обследование. При этом не следует забывать, что статистические характеристики, полученные по выборочной совокупности, всегда имеют вероятностную основу и всегда будут уступать результатам сплошного наблюдения по точности и надежности. Поэтому при подготовке выборочного наблюдения необходимо определить тот минимально необходимый объем выборки, который обеспечит требуемую точность полученных статистических характеристик при заданном уровне вероятности.
Предельную ошибку повторной собственно случайной выборки можно записать через среднюю ошибку:
Отсюда можно вывести формулу для определения необходимого объема собственно случайной повторной выборки:
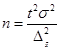 (64)
(64)Полученный на основе использования данной формулы результат всегда округляется в большую сторону. Например, если мы получили, что необходимый объем выборки составляет 598,1 единицы, то для достижения желаемого результата обследованием должны быть охвачены 599 единиц.
Пример 3. Вам необходимо провести исследование с вероятностью 95,4 %, посвященное оценке удовлетворенности качеством работы менеджеров, отвечающих за поддержку клиентов по телефону. Качество обслуживания оценивается клиентами в баллах по пятибалльной шкале. Из прошлых исследований известно, что среднее квадратическое отклонение в оценках качества составляет 0,5 балла. Предельно допустимая ошибка данного исследования не должна превышать 5 %. Какое минимальное количество респондентов вам необходимо опросить в порядке собственно случайной повторной выборки для решения данной проблемы?
Решение:
Поскольку при вероятности 0,954 значение t = 2, находим необходимый объем выборки:
Следовательно, обследованию необходимо подвергнуть не менее 400 респондентов на предмет оценки удовлетворенности качеством работы менеджеров из службы поддержки.
В соответствии с формулой 16 необходимый объем выборки будет тем больше, чем выше заданный уровень вероятности и чем сильнее варьирует наблюдаемый признак. В то же время повышение допустимой предельной ошибки выборки приводит к снижению необходимого ее объема.
При определении необходимого объема выборки для определения границ генеральной доли задача оценки вариации решается значительно проще. Если дисперсия изучаемого альтернативного признака неизвестна, то можно использовать ее максимальное возможное значение:
(65)
Это значение подставляется в формулу 64 в качестве значения дисперсии.
Необходимый объем собственно случайной бесповторной выборки определяется по следующей формуле:
При этом важно помнить, что в процессе проведения вычислений объем генеральной совокупности должен быть выражен только в единицах, а не в тысячах или в миллионах единиц. Например, подставив в данную формулу общее количество заказов, выраженное в тысячах единиц, мы не получим правильное значение необходимой численности выборки, также выраженное в тысячах единиц, как это иногда бывает в других расчетах. Результат вычислений будет неверен.
Пример 4. Требуется определить объем выборки для исследования удовлетворенности постоянных клиентов качеством работы персональных менеджеров с вероятностью 95,4 %. Качество работы оценивается клиентами в баллах по пятибалльной шкале. Из прошлых исследований известно, что среднее квадратическое отклонение в оценках качества составляет 0,5 балла. Предельно допустимая ошибка данного исследования не должна превышать 0,05. Какое минимальное количество постоянных клиентов вам необходимо опросить в порядке собственно случайной бесповторной выборки, если общий список постоянных клиентов компании составляет 1000 человек?
Решение:
Следовательно, для обеспечения репрезентативности данных исследования выборочному обследованию методом бесповторного отбора необходимо подвергнуть не менее 286 постоянных клиентов компании.
Для определения численности механической выборки используют формулы, применяемые при собственно случайном бесповторном отборе. При этом, определив необходимую численность выборки и сопоставив ее с объемом генеральной совокупности, как правило, приходится производить соответствующее округление в меньшую сторону для получения целочисленного интервала отбора.
Пример 5. Вы контролируете работу 284 супермаркетов вашего района. Определим, сколько из них необходимо отобрать в порядке механического отбора для выявления нарушений политики вашей компании с ошибкой +/-2 нарушения и с вероятностью 0,95. По результатам ранее проведенного обследования известно, что среднее квадратическое отклонение численности нарушений составляет 3 единицы.

