ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 03.05.2024
Просмотров: 187
Скачиваний: 0
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
· метод регрессионного анализа – построение модели взаимосвязи, позволяющей получать расчетные значения результативного показателя на основе значений факторного признака.
Причинную обусловленность и корреляцию нельзя считать синонимами. Корреляция не всегда дает объяснение, почему исследуемые переменные в двумерной совокупности связаны между собой. Следует иметь в виду, что корреляция бывает и без причинной обусловленности: она представляет собой число, которое говорит, что большим значениям одного фактора соответствуют большие значения другого (или наоборот). Корреляция всего лишь указывает, что между этими величинами наблюдается определенное соответствие.
Наиболее распространенной причиной существования корреляции без причинной обусловленности является наличие некоторого скрытого третьего фактора, создающего впечатление, будто одна переменная выступает причиной другой. Однако реальной причиной для каждой из этих двух переменных является неизвестная третья.
Под термином ложная корреляция понимают высокую корреляцию, которая обеспечивается действием третьего фактора. Например, если рассчитать значение коэффициента корреляции между такими показателями, как «размер ущерба имуществу от пожара» и «количество пожарных, участвовавших в тушении пожара», то это будет величина, близкая к 1. Однако, конечно же, нельзя утверждать, что причиной высокого размера ущерба является большое количество пожарных, действиями которых и нанесен ущерб имуществу. Безусловно, пожарные, заливая огонь пеной или водой, могут нечаянно повредить электрокабели или офисную технику, но в любом случае причиной высокой корреляции между ущербом имуществу и количеством пожарных является третий фактор – масштаб самого пожара. Чем более сложный и масштабный пожар, тем больший урон имуществу он наносит и тем большее число пожарных требуется для его тушения.
Вопрос 2. Графический метод выявления взаимосвязи.
Графический метод предполагает изображение взаимосвязи двух признаков с помощью диаграммы рассеяния (поля корреляции). Диаграмма рассеяния представляет каждую единицу совокупности в виде точки в пространстве двух измерений, соответствующих двум факторам. Переменная, которая рассматривается как «причина», обозначается
х и указывается на оси абсцисс. Переменная, изменяющаяся под влиянием этой причины, обозначается y и указывается по оси ординат.
Для построения диаграммы рассеяния необходимо в системе координат на оси Х отложить значения факторного признака, а на оси Y – результативного и каждое пересечение линий, проводимых через эти оси, обозначить соответствующими точками. Чем сильнее связь между признаками, тем теснее будут группи
|
роваться точки вокруг определенной линии, выражающей форму связи (рис. 21).

Рис. 21. Диаграмма рассеяния (поле корреляции)
При отсутствии связи диаграмма рассеяния точек имеет вид либо круглого, либо овального облака (причем овал может быть направлен как горизонтально, так и вертикально, но не иметь наклона) (рис. 22).
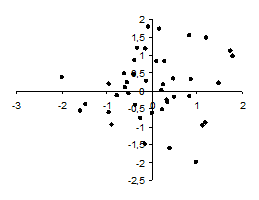
Рис. 22. Диаграмма рассеяния, свидетельствующая об отсутствии взаимосвязи между двумя признаками
Легче всего поддается анализу и интерпретации двумерная совокупность данных, выраженная в форме линейной взаимосвязи. Визуально взаимосвязь проявляется в том, что точки на диаграмме рассеяния концентрируются вокруг условной прямой линии. Они могут как довольно тесно концентрироваться, почти точно попадая на прямую линию (рис. 23), так и быть разбросаны достаточно широко, образуя некоторое облако (рис. 24).
Рис. 23. Диаграмма рассеяния, выражающая линейную положительную взаимосвязь
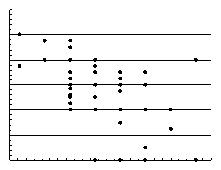
Рис. 24. Диаграмма рассеяния, выражающая линейную отрицательную взаимосвязь
При нелинейной взаимосвязи точки на диаграмме рассеяния группируются вокруг некоторой кривой линии. Поскольку разновидностей кривых линий существует множество, анализ такой взаимосвязи существенно осложнен. Приведем пример двух наиболее распространенных видов нелинейной связи (рис. 25 и 26):
Рис. 25. Диаграмма рассеяния, характеризующая взаимосвязь, выраженную уравнением гиперболы
Рис. 26. Диаграмма рассеяния, характеризующая взаимосвязь, выраженную уравнением параболы
Пример 1. Построим диаграмму рассеяния по данным таблицы 42 и охарактеризуем тип взаимосвязи, которую иллюстрирует диаграмма рассеяния.
Таблица 42.
Итоги работы менеджеров по продаже полиграфической продукции
| Менеджер проекта | Величина списка контактов, тыс. чел. | Объем продаж, тыс. руб. |
| 1 | 168 | 5178 |
| 2 | 21 | 2370 |
| 3 | 94 | 3591 |
| 4 | 39 | 2056 |
| 5 | 249 | 7325 |
| 6 | 43 | 2449 |
| 7 | 589 | 15708 |
| 8 | 41 | 2469 |
При построении диаграммы рассеяния для данной двумерной совокупности данных необходимо, во-первых, определить факторный и результативный признаки. Так как затраченные усилия влияют на результат, следовательно, число контактов с клиентами признаем факторным признаком и изображаем его на горизонтальной оси, а объем продаж – результативным признаком и располагаем его по вертикальной оси. Далее изображаем точки, иллюстрирующие, как величина объема продаж изменяется от количества контактов. Нанеся все точки на график, получим диаграмму рассеяния, которая представлена на рис. 27.
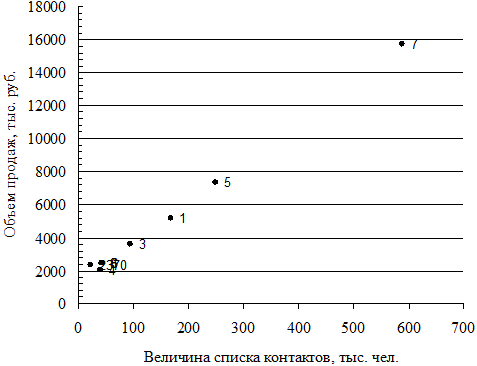
Рис. 27. Взаимосвязь между количеством контактов и объемом продаж полиграфической продукции
На диаграмме рассеяния представлена информация как о каждой отдельной единице совокупности, так и о взаимосвязи между ними. Взаимосвязь между количеством контактов и объемом продаж можно признать положительной: точки на диаграмме выстраиваются снизу вверх при движении слева направо. Это свидетельствует о том, что менеджеры, имеющие больше количество контактов с клиентами, обеспечили компании и большие объемы сбыта (чем больше значения х, тем выше расположены точки на диаграмме). Полученную взаимосвязь можно признать линейной, что видно и по форме области концентрации точек на диаграмме рассеяния, которые практически выстраиваются в прямую линию.
Вопрос 3. Изучение взаимосвязи между качественными признаками.
Значения бизнес-показателей, анализируемых в ходе исследования, не всегда имеют количественное выражение. При обработке информации менеджер-аналитик часто сталкивается с показателями, выраженными в номинальной шкале, например: пол, должность сотрудника, уровень профессионального образования и т.п. Также информация может быть представлена по альтернативным признакам, принимающим только два варианта «да» (1) и «нет» (0) (например: курение сотрудника, наличие или отсутствие у него детей, наличие/отсутствие замечаний за нарушение производственной дисциплины и т.п.). При экспресс-опросах, например, по результатам обучающих мероприятий, используются вопросы, призванные выявить степень удовлетворенности участников обучения его результатами (удовлетворен / не удовлетворен), изменение отношения к предмету обучения (изменилось / не изменилось, ниже среднего / среднее / выше среднего, улучшилось / не изменилось / ухудшилось). Такие показатели являются качественными, и известные методы количественного анализа для их анализа и исследования неприменимы.
Для определения тесноты связи двух качественных признаков, каждый из которых состоит только из двух вариантов, применяются коэффициенты ассоциации и контингенции.
Для их вычисления строится таблица сопряженности [2 х 2], которая показывает связь между двумя явлениями, каждое из которых состоит из двух качественно отличных друг от друга значений признака (например, изделие годное или бракованное). Как правило, в строках располагают варианты факторного признака, а в столбцах – результативного. Если признак один и тот же, а различие состоит в объектах, то в строках и столбцах используют одинаковый порядок расположения вариантов. Например, исследуя взаимосвязь между факторным признаком «наличие высшего образования у родителей (имеют / не имеют)» и «наличие высшего образования у детей (имеют / не имеют)», вариант «имеет высшее образование» следует расположить в первой строке и в первом столбце таблицы сопряженности этих признаков.
Таблица 43.
Таблица взаимной сопряженности для вычисления коэффициентов ассоциации и контингенции
| y x | I | II | Всего: |
| I | n11 | n12 | n11+n12 |
| II | n21 | n22 | n21+n22 |
| Всего: | n11+n21 | n12+n22 | n11+n12+n21+n22 |
Коэффициент ассоциации Ка вычисляют по формуле:
где
n11 – число единиц, имеющих значения x1 и y1;
n12 – число единиц, имеющих значения x1 и y2;
n21 – число единиц, имеющих значения x2и y1;
n22 – число единиц, имеющих значения x2и y2.
Коэффициент ассоциации принимает значения в интервале [-1; 1]. При равенстве коэффициента ассоциации нулю говорят об отсутствии связи между изучаемыми признаками.
Коэффициент контингенции Кк считается более надежной мерой связи и определяется по формуле:
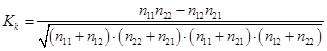 (68)
(68)Коэффициент контингенции принимает значения в интервале [0; 1]. Коэффициент контингенции принимает нулевое значение при отсутствии связи между изучаемыми показателями и равен единице – при функциональной зависимости между ними.
Коэффициент контингенции всегда меньше коэффициента ассоциации. Связь считается подтвержденной, если
Пример 2. Исследуем связь между активностью участия студентов в практических занятиях и результатом тестирования по теме курса. Результаты обследования характеризуются следующими данными (таблица 44).
Таблица 44.
Зависимость результата тестирования по теме от активности участия студентов в практических занятиях
| Участие в практическом занятии | Количество студентов | Из них | |
| успешно сдали тест по теме | не сдали тест по теме | ||
| Активное Пассивное | 100 100 | 78 32 | 22 68 |
| Итого | 200 | 110 | 90 |

