Статистическая обработка выборочных данных

Вариант 9
1. Случайная величина X распределена по закону Коши



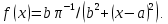
В соответствии с исходными данными параметры распределения Коши:





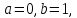
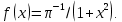
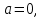
Для получения выборки 100 случайных значений случайной величины распределенной по закону Коши с параметрами 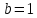воспользуемся отношением двух независимых распределенных по нормальному закону случайных величин 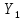, 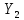с математическим ожиданием 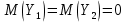и средним квадратическим отклонением .

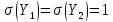Для генерации выборки воспользуемся пакетом анализа табличного процессора MS Office Excel.

N	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16	17	18	19	20
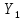	-0,6354071	-0,5837262	2,60391971	0,52204086	-1,4053512	0,94532425	-0,4853905	1,85882527	-0,6270989	-0,541869	1,00552143	0,29599278	0,16246759	0,93734343	-0,0388332	-0,2445722	0,82091447	-0,918867	1,05440904	-0,4262279
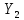	0,10895747	-0,920852	1,12981979	-0,0717785	0,60462753	-2,1051346	0,76108222	0,51451707	0,21214305	0,72967168	0,91910124	1,46871116	-1,5711248	-1,9193976	-0,252146	1,19976221	0,77670848	-1,5220576	0,63325615	-0,3980779
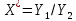	-5,8316987	0,63389795	2,30472127	-7,2729461	-2,3243255	-0,4490564	-0,6377636	3,61275725	-2,9560189	-0,7426203	1,09402684	0,20153233	-0,1034085	-0,4883529	0,15401055	-0,2038506	1,05691452	0,60370058	1,6650593	1,0707148

---

N	21	22	23	24	25	26	27	28	29	30	31	32	33	34	35	36	37	38	39	40
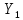	1,214184522	-0,825423285	1,623157004	-0,581007953	-0,98332066	0,440428494	0,832651494	0,343173951	-0,08658958	-0,115270495	-2,068682079	-0,533912043	-0,391214598	0,352113148	0,409863787	0,712212795	1,507601155	0,073926003	-0,693798938	0,220443326
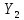	0,183044904	-0,170845169	0,323764198	-1,904645615	-0,130686431	-1,457333383	0,782827101	0,516699856	1,416319719	0,083134637	0,806746812	-0,226168595	1,168759809	-0,062501613	-0,792947503	-0,463132892	0,850636752	-1,18868229	1,23935024	1,504035936
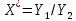	6,633260459	4,831411327	5,013392512	0,305047799	7,524275139	-0,302215333	1,063646741	0,664164983	-0,061137029	-1,386551979	-2,564227152	2,360681613	-0,334726259	-5,633664987	-0,516886409	-1,537815188	1,772320736	-0,062191558	-0,559808612	0,146567858

N	41	42	43	44	45	46	47	48	49	50	51	52	53	54	55	56	57	58	59	60
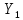	0,342444082	-1,021373919	-0,138173846	-1,862281351	-0,367865596	-0,738284598	-0,649323511	-1,093490027	-0,297592351	-0,902653028	-1,242651706	-1,694597813	0,136628842	-0,827253643	0,767433903	0,898521648	1,464900379	1,293237801	0,2345746	0,10518761
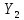	0,346258275	0,7634344	1,535845513	-0,788868419	-1,583066478	-0,977754553	-0,040363375	-0,042584816	-0,107341975	0,197144345	0,551463017	-0,098805231	-0,272575562	0,460664751	-0,970132987	-0,216134595	0,82768338	1,790540409	1,612115739	0,765380719
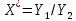	0,988984542	-1,337867299	-0,089965979	2,360699586	0,23237533	0,755081729	16,08694795	25,67793262	2,772376323	-4,578640217	-2,253372695	17,15089173	-0,501251251	-1,795782382	-0,791060518	-4,157231977	1,769880144	0,722261165	0,145507295	0,137431748

---

N	61	62	63	64	65	66	67	68	69	70	71	72	73	74	75	76	77	78	79	80
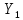	0,16494937	0,191921572	0,569993972	-1,793973752	0,241500402	0,34634013	-2,015767677	1,123758011	-0,753134373	-0,833515514	-0,224207497	-1,714543032	1,013161182	-0,183745215	2,232609404	-1,391319984	1,153748599	0,122357733	-2,802844392	0,913164513
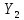	0,621613481	0,366392214	0,584270765	-0,962324975	1,983571565	-1,944117685	-0,950240064	-0,843629095	-0,886784619	-1,228377187	1,09474513	-2,515043889	2,06158802	0,026357156	-1,439213975	1,130542842	0,389068191	-0,260288289	0,313784767	1,158073246
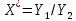	0,265356809	0,523814548	0,975564766	1,864207828	0,121750284	-0,178147718	2,121324655	-1,332052222	0,849286689	0,678550142	-0,204803375	0,681714955	0,491446968	-6,971359558	-1,551269959	-1,230665422	2,96541487	-0,470085433	-8,932378772	0,788520515

---

N	81	82	83	84	85	86	87	88	89	90	91	92	93	94	95	96	97	98	99	100
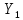	0,105571871	-0,741906661	2,046454028	0,422210178	-0,866118626	-0,858683507	1,339446953	0,31434638	-0,374340061	0,579377684	1,551966307	1,148257525	-1,035655259	1,808302841	-0,125826318	-1,042085387	-0,624120275	0,644420197	1,497664925	0,598943188
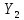	1,073267413	0,208467554	-0,796303539	1,999123924	-1,936077751	-0,180478992	-0,395016286	-0,248752485	0,719130639	0,592274318	-0,475516799	0,818131412	-1,475718818	-0,896689016	-0,45378556	2,360502549	0,289046511	0,669575684	-0,705622369	1,080234142
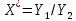	0,098364928	-3,558859137	-2,56994215	0,211197602	0,447357357	4,7578031	-3,390865136	-1,263691415	-0,520545282	0,978225234	-3,263746536	1,403512331	0,701797149	-2,016644352	0,27728145	-0,441467597	-2,159238224	0,962430705	-2,122473706	0,554456821

2. Сгруппируем данные выборки и построим таблицу соответствующего статистического ряда.

Найдем минимальное и максимальное значение в выборке:

---

,

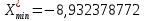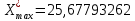
Разобьем полученный интервал на 10 равных и полученное значение шага округлим до тысячных в большую сторону:



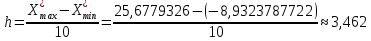
Получим следующие границы интервалов взяв за левую границу первого интервала минимальное значение, округленное до тысячных в большую по модулю сторону:

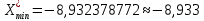
	1		2		3		4		5		6		7		8		9		10
-8,933		-5,471		-2,009		1,453		4,915		8,377		11,839		15,301		18,763		22,225		25,687

Округление в большую по модулю сторону позволяет учесть все 100 значений выборки.

Определим значения вариант (середин интервалов) и частоту попадания значений выборки в данные интервалы:

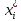	-7,202	-3,74	-0,278	3,184	6,646	10,108	13,57	17,032	20,494	23,956
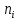	5	13	63	13	3	0	0	2	0	1

---

Смотрите также файлы

• Задача 2 Нарушено удовлетворение потребностей есть, быть здоровым, учиться, спать.docx

• Конспект урока географии в 8 классе по теме Распределение температур и осадков по территории России.doc

• Основные категории специальной психологии и коррекционной педагогики. Их краткая характеристика.ppt

• Тема1 Коррекционная педагогика и коррекционная психология как науки План лекции.docx

• Чулакова София Юрьевна, 41. 03. 01 Зарубежное регионоведение.docx