ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 05.05.2024
Просмотров: 18
Скачиваний: 0
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
, 
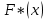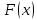- эмпирическая и теоретическая функции распределения исследуемой случайной переменной 
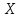.Независимо от вида закона распределения случайной переменной
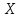функция распределения показателя согласованности имеет вид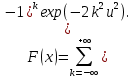
В качестве критической области используется правосторонняя область, границу
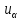которой определяют из условия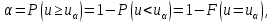 
то есть она равна
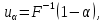
При требуемом уровне значимости (
) 
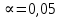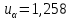
Определим максимальную величину модуля разности ординат эмпирической и теоретической функций распределения и вычислим значение показателя согласованности
:  | |  |  |  |
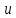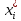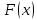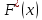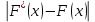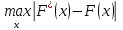| -7,202 | 0,04391664 | 0,05 | 0,00608336 | |
| -3,74 | 0,08316417 | 0,18 | 0,09683583 | |
| -0,278 | 0,41368927 | 0,81 | 0,39631073 | Max |
| 3,184 | 0,90313357 | 0,94 | 0,03686643 | |
| 6,646 | 0,95246166 | 0,97 | 0,01753834 | |
| 10,108 | 0,96861125 | 0,97 | 0,00138875 | |
| 13,57 | 0,97658544 | 0,97 | 0,00658544 | |
| 17,032 | 0,9813325 | 0,99 | 0,0086675 | |
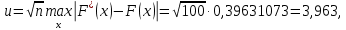
Так как неравенство
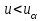не выполняется то гипотеза о соответствии выборочного закона распределения распределению Коши с параметрами
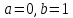отклоняется.6. Даны значения трёх факторов X, Y, Z каждый на двух уровнях (всего 8 наборов значений), для каждого из них известно экспериментальное значение W.
На основе исходных данных план полного факторного эксперимента оформим в виде матрицы планирования.
| № опыта | X | Y | Z | W |
| 1 | -1 | -1 | +1 | 17,71 |
| 2 | +1 | -1 | -1 | 16,24 |
| 3 | -1 | +1 | -1 | 18,87 |
| 4 | +1 | +1 | +1 | 15,16 |
| 5 | -1 | -1 | +1 | 22,82 |
| 6 | +1 | -1 | -1 | 15,17 |
| 7 | -1 | +1 | -1 | 15,71 |
| 8 | +1 | +1 | +1 | 15,26 |
Линейное уравнение регрессии представим в виде полинома:
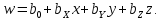
Данный полином содержит один свободный член
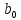и 3 линейных члена 
, 
, 
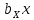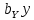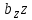. Вычислим соответствующие коэффициенты регрессии: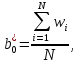
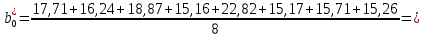
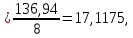
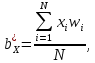
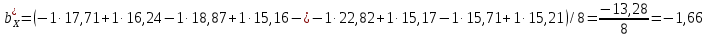
По аналогии с оценкой коэффициента регрессии
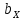, найдем остальные: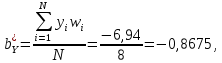
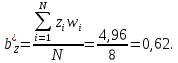
Таким образом линейное уравнение регрессии примет вид:
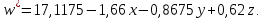
Литература
1. Гмурман В.Е. Руководство к решению задач по теории вероятностей, математической статистике и случайным функциям. М., 2002.
2. Ткачев А.Н., Некрасов С.А. Теория вероятностей и ее приложения. Учебное пособие. На компьютерном носителе (сервер лаборатории ЭВМ кафедры ПМ).
3. Ткачев А.Н., Некрасов С.А. Теория вероятностей и ее приложения. Учебное пособие. Новочеркасск, ЮРГТУ (НПИ), 2007.