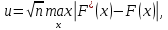ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 05.05.2024
Просмотров: 17
Скачиваний: 0
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
3. Так-как варианты являются равноотстоящими, для вычисления выборочных среднего, дисперсии, асимметрии и эксцесса удобно воспользоваться методом произведений, то есть использовать следующие формулы:
, 
, 
, 
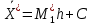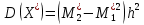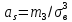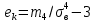,где
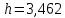– шаг (разность между двумя соседними вариантами); С – ложный нуль (выберем варианту (-0,278), которая имеет наибольшую частоту); 
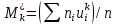– условные моменты 
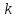-го порядка; 
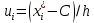– условная варианта; 
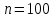общий объем выборки; 
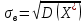– выборочное среднее квадратическое отклонение; 
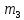и 
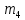– центральные эмпирические моменты третьего и четвертого порядков которые в случае равноотстоящих вариант удобно вычислять по формулам:
, 
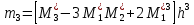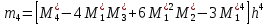.Составим расчетную таблицу:
 |  |  |  |  |  |  |  |  |
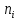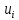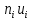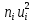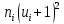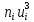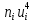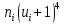| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| -7,202 | 5 | -2 | -10 | 20 | 5 | -40 | 80 | 5 |
| -3,74 | 13 | -1 | -13 | 13 | 0 | -13 | 13 | 0 |
| -0,278 | 63 | 0 | 0 | 0 | 63 | 0 | 0 | 63 |
| 3,184 | 13 | 1 | 13 | 13 | 52 | 13 | 13 | 208 |
| 6,646 | 3 | 2 | 6 | 12 | 27 | 24 | 48 | 243 |
| 10,108 | 0 | 3 | 0 | 0 | 0 | 0 | 0 | 0 |
| 13,57 | 0 | 4 | 0 | 0 | 0 | 0 | 0 | 0 |
| 17,032 | 2 | 5 | 10 | 50 | 72 | 250 | 1250 | 2592 |
| 20,494 | 0 | 6 | 0 | 0 | 0 | 0 | 0 | 0 |
| 23,956 | 1 | 7 | 7 | 49 | 64 | 343 | 2401 | 4096 |
| |  | |  |  |  |  |  |  |
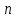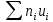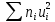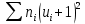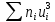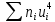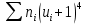| 100 | | 13 | 157 | 283 | 577 | 3805 | 7207 |
Столбцы 6 и 9 служат для контроля вычислений с помощью тождеств:
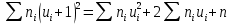, 283=283
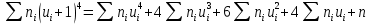, 7207=7207,совпадение контрольных сумм свидетельствует о правильности вычислений.
Вычислим условные моменты первого, второго, третьего и четвертого порядков:
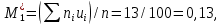
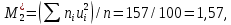
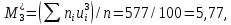
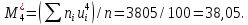
Вычислим центральные эмпирические моменты третьего и четвертого порядков
,
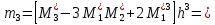
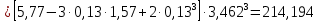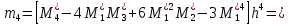
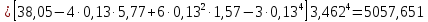.Определим искомые значения выборочных среднего, дисперсии, асимметрии и эксцесса:
,
,
,
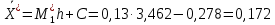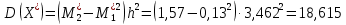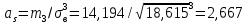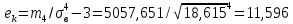.Построим гистограмму и график эмпирической функции распределения.
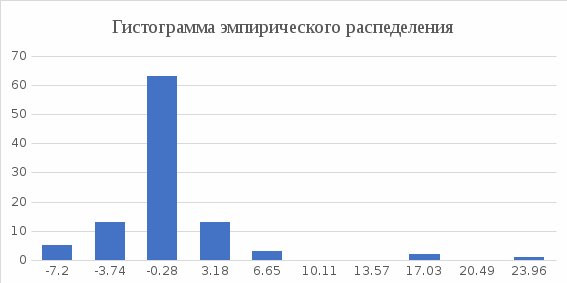
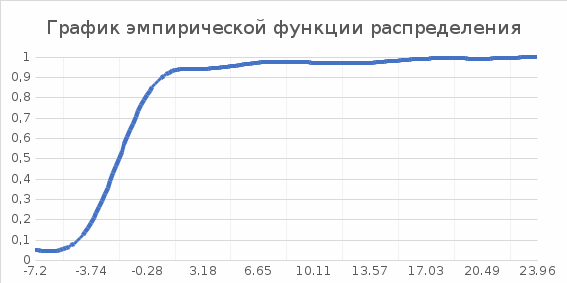
4. Для выборочного среднего доверительный интервал с надежностью 0,95 определяется выражением:
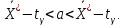
При неизвестном
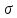определим 
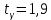по приложению 2 Руководства к решению задач по теории вероятностей, математической статистике и случайным функциям [1] с параметрам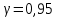и
и 
. Таким образом, доверительные интервалы для выборочного среднего представим в виде: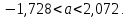
Для построения доверительного интервала дисперсии с надежностью 0,95 воспользуемся приложением 4 Руководства к решению задач по теории вероятностей, математической статистике и случайным функциям [1] и определим
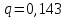(входом в приложение являются параметры 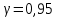и . Так как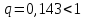 
, доверительный интервал определяется выражением: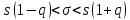
где
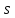– исправленная выборочное среднее квадратическое отклонение: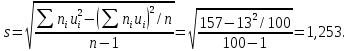
Таким образом, доверительные интервалы для выборочного среднего квадратического отклонения представим в виде:
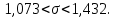
5. Выдвинем статистическую гипотезу о соответствии выборочного закона распределения распределению Коши с параметрами
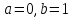:Теоретическая функции распределения Коши определяется выражением:
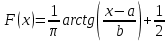
Или в соответствии с заданными параметрами:
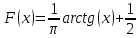
Для проверки гипотезы методом К. Пирсона результаты испытаний представим в виде таблицы (смотри пункт 2) и дополним их вероятностями
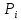попадания случайной величины 
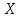в соответствии с теоретическим законом распределения в 
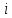-ый интервал: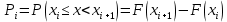
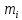 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | ||||||||||
| -8,933 | -5,471 | -2,009 | 1,453 | 4,915 | 8,377 | 11,839 | 15,301 | 18,763 | 22,225 | 25,687 | ||||||||||
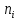| | 5 | 13 | 63 | 13 | 3 | 0 | 0 | 2 | 0 | 1 | ||||||||||
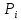| | 0,022 | 0,089 | 0,661 | 0,128 | 0,026 | 0,011 | 0,006 | 0,004 | 0,003 | 0,002 | ||||||||||
В качестве показателя согласованности используем случайную величину
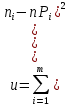
где
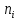- число результатов испытаний, попавших в 
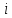-ый интервал; 
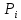- вероятность попадания результата испытания в 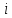-ый интервал при теоретическом законе распределения исследуемой переменной 
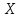.Вычислим значение показателя согласованности
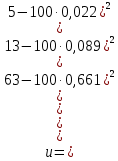
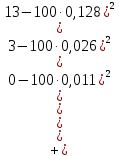
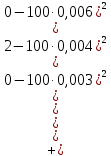
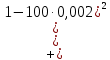
Показатель согласованности имеет
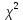-распределение с числом степеней свободы 
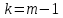, где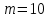 
– количество интервалов разбиения эмпирических данных. При требуемом уровне значимости (
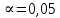) и числом степеней свободы 
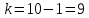определим в соответствии с приложением 5 Руководства к решению задач по теории вероятностей, математической статистике и случайным функциям [1] значение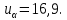 
В качестве критической целесообразно выбрать правостороннюю критическую область
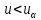.Так как неравенство
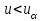не выполняется то гипотезе о том, что эмпирическое распределение подчиняется закону Коши бракуется.При проверке гипотез методом А.Н. Колмогорова в качестве показателя согласованности принимают случайную величину
