Файл: Работы Индивидуальное задание вариант 76. Номер варианта по дисциплине Прикладная физика в электроэнергетике Наименование учебной дисциплины.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 17.10.2024
Просмотров: 67
Скачиваний: 0
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
2 – индукция поля создаваемого током I2.
Если B1 и В2 направлены по одной прямой, то векторная сумма может быть заменена алгебраической суммой:
В = В1+В2. (1)
При этом слагаемые В1и В2должны быть взяты с соответствующими знаками. Вычислим эти индукции по формуле
B1 = 0I1/(2a), B2 = 0I2/(2( r - a)), (2)
где 0 = 4 10 -7 Гн/м.
Подставив значения величин в формулs (2), найдём модули В1 и В2:
В1 = 72,73 мкТл,
В2 = 106,67 мкТл.
1-й случай. Векторы B1 и В2 направлены по одной прямой (рис. 3.3, а); следовательно, результирующая индукция В определяется по формуле (1). Приняв направление вверх положительным, вниз – отрицательным, запишем: В1 = -72,73 мкТл, В2 = 106,87 мкТл.
Подставив в формулу (1) эти значения В1и B2, получим
В = В1+В2 = 33,94.
2-й случай. Векторы В1 и В2 направлены по одной прямой в одну сторону (рис. 3.3, б) и их значения отрицательны..
Подставив в формулу (1) значения B1 и В2 получим
В = В1+В2 = -179,4 мкТл.
3-й случай. Векторы индукций магнитных полей, создаваемых токами в точке а = 0,55rот вертикального провода взаимно перпендикулярны (рис. 3.3, в). Результирующая индукция по модулю и направлению является диагональю прямоугольника, построенного на векторах В1 и В2, создаваемые токами I1, I2, соответственно. Вектор В1 = 0I1/(2ar). Подставив значения, получим В1 = 72,73 мкТл. Если подумать, то для индукции В2 справедлива формула (2), то есть В2 = 106,67 мкТл.


Рис. 3.4
По теореме Пифагора найдём
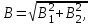 (3)
(3)
Подставив в формулу (3) значения В1и В2и вычислив, получим
B = 129,11 мкТл.
Пример 3.3. Определить магнитную индукцию В поля, создаваемого отрезком бесконечно длинного прямого провода, в точке, равноудалённой от концов отрезка и находящейся на расстоянии r0 = 20 см от середины его (рис. 3.4). Сила тока I, текущего по проводу, равна 30 А, длина l отрезка равна 60 см. Определить во сколько раз магнитная индукция В больше в точке r0/2, то есть на половине расстоянияr0.
Решение. Для определения магнитной индукции поля, создаваемого отрезком провода, воспользуемся законом Био –Савара–Лапласа:
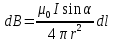 . (1)
. (1)
Прежде чем интегрировать выражение (1), преобразуем его так, чтобы можно было интегрировать по углу . Для этого выразим приращение длины проводника, то есть элемент dl,через приращение угла d. Согласно рис. 3.4, запишем
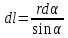
Подставим это выражение dl в формулу (1), имеем:
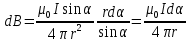 .
.
Но r – величина переменная, зависящая от и равная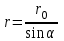 . Подставив значение rв предыдущую формулу, найдём
. Подставив значение rв предыдущую формулу, найдём
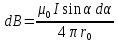 . (2)
. (2)
Чтобы определить магнитную индукцию поля, создаваемого отрезком проводника, проинтегрируем выражение (2) в пределах от 1 до 2:
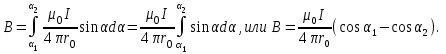 (3)
(3)
Заметим, что при симметричном расположении точки A относительно отрезка провода cos 2 = – cos 1. С учётом этого формула (3) примет вид
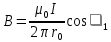 (4)
(4)
Из рис. 3.4 следует
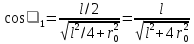 .
.
Подставив выражение cos 1 в формулу (4), получим
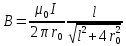 . (5)
. (5)
Подставим числовые значения в формулу (5) и произведём вычисления:
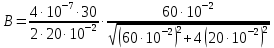
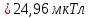
На половине расстояния r0/2 магнитная индукция В в 2,28 раза больше.
Задача 3.1
Задача 3.2
Задача 3.3
Если B1 и В2 направлены по одной прямой, то векторная сумма может быть заменена алгебраической суммой:
В = В1+В2. (1)
При этом слагаемые В1и В2должны быть взяты с соответствующими знаками. Вычислим эти индукции по формуле
B1 = 0I1/(2a), B2 = 0I2/(2( r - a)), (2)
где 0 = 4 10 -7 Гн/м.
Подставив значения величин в формулs (2), найдём модули В1 и В2:
В1 = 72,73 мкТл,
В2 = 106,67 мкТл.
1-й случай. Векторы B1 и В2 направлены по одной прямой (рис. 3.3, а); следовательно, результирующая индукция В определяется по формуле (1). Приняв направление вверх положительным, вниз – отрицательным, запишем: В1 = -72,73 мкТл, В2 = 106,87 мкТл.
Подставив в формулу (1) эти значения В1и B2, получим
В = В1+В2 = 33,94.
2-й случай. Векторы В1 и В2 направлены по одной прямой в одну сторону (рис. 3.3, б) и их значения отрицательны..
Подставив в формулу (1) значения B1 и В2 получим
В = В1+В2 = -179,4 мкТл.
3-й случай. Векторы индукций магнитных полей, создаваемых токами в точке а = 0,55rот вертикального провода взаимно перпендикулярны (рис. 3.3, в). Результирующая индукция по модулю и направлению является диагональю прямоугольника, построенного на векторах В1 и В2, создаваемые токами I1, I2, соответственно. Вектор В1 = 0I1/(2ar). Подставив значения, получим В1 = 72,73 мкТл. Если подумать, то для индукции В2 справедлива формула (2), то есть В2 = 106,67 мкТл.


Рис. 3.4
По теореме Пифагора найдём
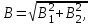 (3)
(3)Подставив в формулу (3) значения В1и В2и вычислив, получим
B = 129,11 мкТл.
Пример 3.3. Определить магнитную индукцию В поля, создаваемого отрезком бесконечно длинного прямого провода, в точке, равноудалённой от концов отрезка и находящейся на расстоянии r0 = 20 см от середины его (рис. 3.4). Сила тока I, текущего по проводу, равна 30 А, длина l отрезка равна 60 см. Определить во сколько раз магнитная индукция В больше в точке r0/2, то есть на половине расстоянияr0.
Решение. Для определения магнитной индукции поля, создаваемого отрезком провода, воспользуемся законом Био –Савара–Лапласа:
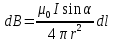 . (1)
. (1)Прежде чем интегрировать выражение (1), преобразуем его так, чтобы можно было интегрировать по углу . Для этого выразим приращение длины проводника, то есть элемент dl,через приращение угла d. Согласно рис. 3.4, запишем
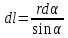
Подставим это выражение dl в формулу (1), имеем:
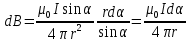 .
.Но r – величина переменная, зависящая от и равная
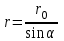 . Подставив значение rв предыдущую формулу, найдём
. Подставив значение rв предыдущую формулу, найдём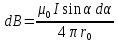 . (2)
. (2)Чтобы определить магнитную индукцию поля, создаваемого отрезком проводника, проинтегрируем выражение (2) в пределах от 1 до 2:
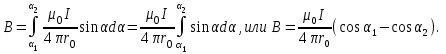 (3)
(3)Заметим, что при симметричном расположении точки A относительно отрезка провода cos 2 = – cos 1. С учётом этого формула (3) примет вид
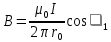 (4)
(4)Из рис. 3.4 следует
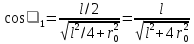 .
.Подставив выражение cos 1 в формулу (4), получим
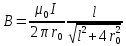 . (5)
. (5)Подставим числовые значения в формулу (5) и произведём вычисления:
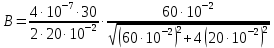
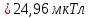
На половине расстояния r0/2 магнитная индукция В в 2,28 раза больше.
Задача 3.1
| Вариант № | Ток I, А | d, см | г1, см | r2, см |
| 1 | 70,4 | 13,7 | 9,96 | 23,36 |
| 2 | 70,6 | 12,9 | 6,73 | 17,83 |
| 3 | 65,4 | 12,5 | 7,75 | 18,15 |
| 4 | 60,1 | 11,4 | 5,06 | 13,26 |
| 5 | 71 | 12 | 9,34 | 17,84 |
| 6 | 69,3 | 13,8 | 9,32 | 21,92 |
| 7 | 61,5 | 12,6 | 7,5 | 19,5 |
| 8 | 61,5 | 13,9 | 6,44 | 19,74 |
| 9 | 65 | 13,8 | 8,94 | 20,94 |
| 10 | 60,4 | 12,6 | 8,84 | 19,44 |
| 11 | 71,7 | 13,3 | 5,92 | 18,32 |
| 12 | 65 | 10,8 | 6,44 | 17,24 |
| 13 | 60,6 | 12,2 | 5,04 | 14,24 |
| 14 | 69,9 | 13,8 | 6,86 | 20,26 |
| 15 | 65,8 | 13,3 | 6,61 | 18,81 |
| 16 | 63,9 | 12,6 | 6,96 | 16,36 |
| 17 | 60,6 | 11,2 | 6,06 | 17,16 |
| 18 | 65,6 | 12,4 | 9,09 | 20,79 |
| 19 | 66 | 13,3 | 5,29 | 17,39 |
| 20 | 64,6 | 13,7 | 5,79 | 16,69 |
| 21 | 62,9 | 11,5 | 5,26 | 15,56 |
| 22 | 61,8 | 12,9 | 9,16 | 22,06 |
| 23 | 68,7 | 10,4 | 8,16 | 15,46 |
| 24 | 62,3 | 10,4 | 7,78 | 17,48 |
| 25 | 71,3 | 10,3 | 6,33 | 16,43 |
| 26 | 68,4 | 13,3 | 5,71 | 17,11 |
| 27 | 64,6 | 11,3 | 7,51 | 18,61 |
| 28 | 61 | 13,7 | 8,71 | 21,01 |
| 29 | 65,8 | 10,3 | 8,56 | 16,96 |
| 30 | 60,5 | 14 | 5,97 | 19,87 |
| 31 | 68,3 | 12,9 | 7,72 | 19,42 |
| 32 | 66,4 | 10,6 | 7,47 | 15,97 |
| 33 | 60 | 13,7 | 6,91 | 17,81 |
| 34 | 63 | 12,3 | 7,73 | 20,03 |
| 35 | 66,7 | 13,2 | 5,51 | 15,41 |
| 36 | 63,3 | 11,7 | 7,45 | 15,25 |
| 37 | 70 | 13,6 | 6,36 | 17,96 |
| 38 | 64,8 | 11,3 | 7,47 | 15,97 |
| 39 | 68,7 | 12,7 | 6,65 | 17,95 |
| 40 | 69,1 | 13,7 | 7,64 | 18,94 |
| 41 | 61,3 | 13,1 | 7,51 | 18,41 |
| 42 | 60,4 | 12,6 | 5,96 | 17,06 |
| 43 | 62 | 11,8 | 9,77 | 18,67 |
| 44 | 71,1 | 12,3 | 5,86 | 17,36 |
| 45 | 63,3 | 13,4 | 7,23 | 17,73 |
| 46 | 70,8 | 13,7 | 5,02 | 15,02 |
| 47 | 67 | 13,1 | 9,83 | 22,63 |
| 48 | 68,9 | 12,9 | 6,97 | 19,87 |
| 49 | 66,4 | 13,3 | 6,06 | 17,56 |
| 50 | 69,5 | 11,8 | 8,95 | 19,35 |
| 51 | 70,2 | 13,8 | 7,81 | 19,01 |
| 52 | 64,2 | 11 | 7,35 | 17,05 |
| 53 | 66,6 | 12,3 | 6,12 | 14,62 |
| 54 | 70,8 | 12,5 | 6,52 | 15,62 |
| 55 | 70,5 | 11,1 | 7,03 | 15,53 |
| 56 | 71,7 | 12,6 | 8,41 | 20,01 |
| 57 | 62,7 | 12,3 | 6,55 | 18,15 |
| 58 | 60,3 | 13,6 | 7,76 | 19,96 |
| 59 | 65,9 | 12,6 | 5,36 | 14,56 |
| 60 | 67,2 | 12,8 | 9,17 | 20,77 |
| 61 | 62,8 | 10,5 | 7,98 | 16,48 |
| 62 | 64,4 | 13,4 | 5,4 | 15,1 |
| 63 | 61,6 | 12,1 | 7,89 | 16,59 |
| 64 | 71,4 | 10,5 | 5,86 | 15,36 |
| 65 | 71,3 | 13,3 | 9,75 | 22,05 |
| 66 | 69,7 | 11,2 | 9,21 | 20,01 |
| 67 | 62 | 12,6 | 5,93 | 15,63 |
| 68 | 62 | 12,3 | 5,86 | 17,66 |
| 69 | 66,6 | 10,5 | 5,39 | 11,99 |
| 70 | 62,3 | 13,4 | 9,26 | 20,36 |
| 71 | 69,9 | 10,1 | 8,73 | 17,63 |
| 72 | 60,8 | 11 | 6,57 | 14,27 |
| 73 | 64,7 | 11,7 | 8,12 | 16,62 |
| 74 | 71,5 | 11,7 | 8,93 | 20,43 |
| 75 | 66,8 | 10,7 | 5,48 | 12,58 |
| 76 | 66,6 | 10,8 | 8,27 | 18,87 |
| 77 | 71 | 12,5 | 7,59 | 17,59 |
| 78 | 66,9 | 11,3 | 9,17 | 17,07 |
| 79 | 70,4 | 11 | 5,01 | 14,31 |
| 80 | 70,5 | 12,5 | 5,27 | 16,87 |
| 81 | 64,1 | 12,3 | 6,35 | 14,95 |
| 82 | 65,6 | 11 | 9,51 | 16,81 |
| 83 | 61,9 | 13,9 | 9,3 | 22,7 |
| 84 | 72 | 12,2 | 7,64 | 18,94 |
| 85 | 62,9 | 13,3 | 5,13 | 18,33 |
| 86 | 67,6 | 13,8 | 5,84 | 19,64 |
| 87 | 62,9 | 13 | 7,53 | 17,53 |
| 88 | 64,1 | 10,6 | 8,81 | 16,61 |
| 89 | 68,7 | 13 | 5,8 | 17,4 |
| 90 | 69,6 | 12,9 | 7,6 | 20 |
| 91 | 71,9 | 10,4 | 9,11 | 18,41 |
| 92 | 69,5 | 12 | 7,39 | 19,29 |
| 93 | 61,3 | 12,7 | 8,29 | 19,69 |
| 94 | 60,8 | 11,2 | 9,24 | 19,94 |
| 95 | 66,3 | 10,8 | 7,07 | 14,87 |
| 96 | 60,5 | 12,6 | 8,53 | 17,73 |
| 97 | 70,1 | 12,1 | 7,22 | 16,42 |
| 98 | 60,1 | 12,2 | 6,29 | 15,79 |
| 99 | 70,3 | 10 | 9,54 | 16,14 |
| 100 | 64,4 | 11,2 | 8,38 | 16,18 |
Задача 3.2
| Вариант № | r, см | Ток I1, А | Ток I2, А | Точка а |
| 1 | 5,26 | 11,91 | 14,6 | 0,55 |
| 2 | 5,62 | 11,54 | 14,12 | 0,84 |
| 3 | 5,81 | 11,56 | 14,52 | 0,71 |
| 4 | 6,03 | 11,01 | 12,62 | 0,79 |
| 5 | 6,47 | 10,06 | 12,58 | 0,8 |
| 6 | 6,65 | 11,99 | 12,75 | 0,88 |
| 7 | 6,42 | 10,49 | 13,31 | 0,84 |
| 8 | 6,36 | 11,31 | 13,23 | 0,83 |
| 9 | 6,84 | 10,8 | 12,89 | 0,56 |
| 10 | 5,64 | 11,68 | 12,61 | 0,7 |
| 11 | 5,24 | 10,79 | 12,56 | 0,87 |
| 12 | 5,67 | 10,62 | 14,28 | 0,68 |
| 13 | 6,89 | 10,89 | 12,41 | 0,62 |
| 14 | 5,57 | 11,9 | 12,98 | 0,75 |
| 15 | 6,64 | 10,09 | 13,07 | 0,59 |
| 16 | 5,49 | 10,76 | 12,3 | 0,8 |
| 17 | 5,3 | 10,29 | 12,43 | 0,71 |
| 18 | 6,37 | 11,32 | 13,54 | 0,85 |
| 19 | 6,53 | 10,75 | 14,09 | 0,82 |
| 20 | 5,77 | 11,64 | 14,29 | 0,68 |
| 21 | 5,77 | 10,93 | 14,13 | 0,84 |
| 22 | 5,37 | 11,12 | 14,64 | 0,73 |
| 23 | 6,8 | 10,53 | 14,67 | 0,74 |
| 24 | 6,45 | 10,02 | 14,31 | 0,81 |
| 25 | 5,77 | 10,84 | 14,78 | 0,86 |
| 26 | 6,4 | 11,93 | 12,6 | 0,64 |
| 27 | 6,88 | 10,76 | 12,95 | 0,82 |
| 28 | 5,33 | 10,03 | 14,53 | 0,77 |
| 29 | 5,84 | 10,95 | 13,29 | 0,78 |
| 30 | 6,85 | 10,33 | 13,89 | 0,82 |
| 31 | 6,31 | 11,21 | 13,53 | 0,83 |
| 32 | 5,93 | 11,49 | 14,17 | 0,66 |
| 33 | 6,01 | 10,33 | 13,92 | 0,64 |
| 34 | 6,68 | 10,63 | 14,59 | 0,66 |
| 35 | 6,74 | 10,16 | 14,81 | 0,76 |
| 36 | 5,84 | 11,66 | 12,49 | 0,79 |
| 37 | 5,55 | 10,35 | 14,33 | 0,83 |
| 38 | 5,1 | 11,67 | 14,77 | 0,87 |
| 39 | 5,32 | 11,87 | 13,51 | 0,68 |
| 40 | 6,18 | 11,16 | 12,18 | 0,67 |
| 41 | 6,63 | 10,7 | 14,55 | 0,78 |
| 42 | 6,26 | 11,28 | 12,2 | 0,76 |
| 43 | 5,29 | 10,26 | 14,07 | 0,62 |
| 44 | 5,75 | 10,13 | 14,83 | 0,71 |
| 45 | 6,73 | 11,22 | 12,26 | 0,72 |
| 46 | 5,68 | 11,42 | 14,51 | 0,83 |
| 47 | 6,44 | 11,49 | 13,31 | 0,72 |
| 48 | 6,12 | 10,3 | 13,09 | 0,6 |
| 49 | 6,45 | 10,05 | 13,14 | 0,68 |
| 50 | 5,94 | 10,58 | 13,13 | 0,66 |
| 51 | 6,04 | 11,58 | 12,05 | 0,86 |
| 52 | 5,57 | 11,34 | 13,18 | 0,79 |
| 53 | 6,29 | 10,07 | 14,71 | 0,59 |
| 54 | 6,83 | 10,38 | 14,95 | 0,85 |
| 55 | 6,34 | 10,69 | 12,01 | 0,84 |
| 56 | 5,31 | 10,55 | 12,83 | 0,69 |
| 57 | 5,92 | 10,12 | 13,12 | 0,63 |
| 58 | 6,09 | 11,22 | 13,71 | 0,77 |
| 59 | 6,69 | 10,04 | 14,29 | 0,65 |
| 60 | 6,23 | 10,28 | 13,81 | 0,58 |
| 61 | 6,3 | 10,6 | 12,49 | 0,81 |
| 62 | 6,23 | 11,24 | 13,09 | 0,86 |
| 63 | 6,85 | 10,66 | 12,89 | 0,58 |
| 64 | 5,22 | 11,31 | 14,26 | 0,82 |
| 65 | 6,17 | 11,29 | 14,09 | 0,6 |
| 66 | 5,51 | 10,44 | 13,69 | 0,59 |
| 67 | 5,2 | 10,04 | 13,21 | 0,68 |
| 68 | 5,77 | 11,88 | 12,55 | 0,74 |
| 69 | 5,11 | 11 | 13,02 | 0,81 |
| 70 | 5,24 | 10,73 | 14,29 | 0,73 |
| 71 | 5,31 | 10,5 | 12,01 | 0,7 |
| 72 | 6,83 | 10,05 | 13,65 | 0,57 |
| 73 | 6,03 | 11,12 | 12,74 | 0,71 |
| 74 | 5,32 | 10,65 | 13,49 | 0,87 |
| 75 | 5,27 | 10,2 | 13,88 | 0,7 |
| 76 | 6,98 | 10,02 | 12,05 | 0,77 |
| 77 | 5,93 | 10,08 | 14,86 | 0,62 |
| 78 | 5,84 | 11,16 | 13,95 | 0,8 |
| 79 | 6,09 | 10,54 | 14,29 | 0,74 |
| 80 | 6,5 | 11,82 | 14,08 | 0,81 |
| 81 | 5,01 | 10,16 | 14,17 | 0,57 |
| 82 | 6,51 | 11,86 | 12,26 | 0,72 |
| 83 | 6,22 | 11,28 | 12,7 | 0,82 |
| 84 | 5,25 | 10,72 | 13,68 | 0,57 |
| 85 | 5,32 | 11,22 | 12,73 | 0,88 |
| 86 | 5,39 | 11,03 | 14,77 | 0,6 |
| 87 | 6,55 | 10,37 | 13,15 | 0,55 |
| 88 | 6,85 | 11,84 | 13,66 | 0,8 |
| 89 | 6,61 | 10,05 | 12,17 | 0,62 |
| 90 | 6,04 | 11,8 | 13,95 | 0,74 |
| 91 | 6,57 | 11,96 | 13,06 | 0,66 |
| 92 | 6,53 | 10,59 | 14,6 | 0,73 |
| 93 | 6,28 | 11,29 | 12,87 | 0,86 |
| 94 | 6,14 | 11,94 | 13,05 | 0,65 |
| 95 | 5,84 | 10,36 | 12,08 | 0,86 |
| 96 | 7 | 11,25 | 12,1 | 0,75 |
| 97 | 5,7 | 11,48 | 14,24 | 0,87 |
| 98 | 6,31 | 10,62 | 14,16 | 0,57 |
| 99 | 5,62 | 10,23 | 14,67 | 0,59 |
| 100 | 6,05 | 10,67 | 14,08 | 0,7 |
Задача 3.3
| Вариант № | r, см | Ток I, А | l, см |
| 1 | 24,8 | 31,9 | 67,1 |
| 2 | 24,5 | 30,5 | 62,5 |
| 3 | 23,8 | 32,6 | 69,4 |
| 4 | 24,2 | 32,3 | 68,6 |
| 5 | 20,1 | 33,9 | 65,3 |
| 6 | 21,4 | 34,1 | 63,7 |
| 7 | 23,2 | 30,3 | 66,4 |
| 8 | 24,7 | 39,1 | 63,3 |
| 9 | 24,1 | 32,2 | 69,9 |
| 10 | 23,2 | 37,3 | 62,5 |
| 11 | 24,2 | 32,2 | 64,4 |
| 12 | 22,2 | 34,7 | 60,1 |
| 13 | 20,3 | 39,1 | 60,8 |
| 14 | 21,7 | 33,8 | 69,7 |
| 15 | 22,9 | 31,8 | 63,8 |
| 16 | 23,5 | 34,3 | 60,9 |
| 17 | 22,8 | 34,8 | 61,2 |
| 18 | 20,3 | 32,8 | 60,1 |
| 19 | 21,9 | 37,7 | 60,4 |
| 20 | 20,7 | 30,1 | 63,3 |
| 21 | 21,5 | 34,8 | 68,5 |
| 22 | 21,4 | 37 | 61,4 |
| 23 | 22,6 | 33,6 | 61,5 |
| 24 | 22,8 | 32,9 | 64,3 |
| 25 | 23 | 36,6 | 68,7 |
| 26 | 21 | 35,8 | 65,5 |
| 27 | 24,3 | 38,2 | 69,3 |
| 28 | 23,4 | 31,2 | 60,1 |
| 29 | 22,5 | 38,9 | 64,1 |
| 30 | 23,8 | 33,3 | 69,2 |
| 31 | 23,4 | 33,9 | 64,5 |
| 32 | 24,8 | 30,5 | 61,5 |
| 33 | 20,9 | 38,6 | 66,2 |
| 34 | 21,6 | 35 | 67,4 |
| 35 | 23,5 | 30,3 | 66,7 |
| 36 | 24,5 | 33,6 | 63,2 |
| 37 | 22,9 | 36,4 | 62,9 |
| 38 | 22,8 | 37,8 | 67,3 |
| 39 | 22,9 | 36,2 | 66,2 |
| 40 | 24,3 | 37,3 | 68,1 |
| 41 | 24,1 | 34,7 | 69,2 |
| 42 | 22,3 | 38,4 | 63,6 |
| 43 | 24,2 | 36,2 | 69,6 |
| 44 | 20,4 | 31,7 | 60,6 |
| 45 | 23,6 | 35,6 | 64,9 |
| 46 | 23,9 | 30,7 | 60,4 |
| 47 | 22,3 | 30,5 | 69,2 |
| 48 | 22,7 | 31,2 | 64,1 |
| 49 | 20,3 | 39,6 | 66,5 |
| 50 | 24,1 | 34,5 | 66,4 |
| 51 | 24,3 | 34,5 | 68 |
| 52 | 22,9 | 38,5 | 61,6 |
| 53 | 22,9 | 31,7 | 66,1 |
| 54 | 22,4 | 38,6 | 68,3 |
| 55 | 21,2 | 39,2 | 65,9 |
| 56 | 21,9 | 36,9 | 62,5 |
| 57 | 22,2 | 34,5 | 66 |
| 58 | 21,1 | 34,1 | 62,5 |
| 59 | 24,3 | 39,6 | 60,7 |
| 60 | 20 | 32,6 | 60,6 |
| 61 | 24,2 | 38,3 | 62,5 |
| 62 | 22,1 | 32,3 | 69,1 |
| 63 | 22,7 | 31,1 | 62,1 |
| 64 | 23 | 39,2 | 66 |
| 65 | 20,2 | 36,6 | 66,8 |
| 66 | 24,1 | 30,8 | 64,4 |
| 67 | 23,4 | 36,3 | 62,6 |
| 68 | 22,3 | 35 | 65 |
| 69 | 22,7 | 39,1 | 68,6 |
| 70 | 20,8 | 33,1 | 61,9 |
| 71 | 22,1 | 36,8 | 69,1 |
| 72 | 20,4 | 36,4 | 60,6 |
| 73 | 20,7 | 37,4 | 61 |
| 74 | 24,4 | 35,9 | 61,3 |
| 75 | 22,7 | 34 | 65,5 |
| 76 | 20,4 | 34 | 65 |
| 77 | 23,3 | 36,8 | 68,2 |
| 78 | 21,6 | 34,8 | 63,9 |
| 79 | 22,5 | 35,7 | 67,7 |
| 80 | 20,7 | 37,8 | 66,2 |
| 81 | 23,3 | 38,2 | 68,3 |
| 82 | 21,2 | 38,6 | 60,9 |
| 83 | 20 | 31,3 | 63 |
| 84 | 24,7 | 32 | 66,2 |
| 85 | 20,7 | 37 | 67 |
| 86 | 24,8 | 38,6 | 61,1 |
| 87 | 24,3 | 33,4 | 65,2 |
| 88 | 23,9 | 38,4 | 64,4 |
| 89 | 24,1 | 33,2 | 63,2 |
| 90 | 21 | 35,2 | 64,2 |
| 91 | 22,3 | 38,9 | 62,6 |
| 92 | 22,1 | 30,4 | 69,5 |
| 93 | 22,3 | 32 | 60,6 |
| 94 | 23,4 | 37,2 | 60,2 |
| 95 | 22 | 35,7 | 60,8 |
| 96 | 21,2 | 36,4 | 68,2 |
| 97 | 21 | 31,8 | 60,8 |
| 98 | 20 | 32,6 | 61,3 |
| 99 | 20,9 | 37 | 69,6 |
| 100 | 22,9 | 34,7 | 68,7 |

