Файл: Работы Индивидуальное задание вариант 76. Номер варианта по дисциплине Прикладная физика в электроэнергетике Наименование учебной дисциплины.docx

---

4. Силы, действующие на движущиеся заряды в магнитном поле

Основные формулы

• Закон Ампера. Сила, действующая на проводник с током в магнитном поле,

F = [lB]I

где I– сила тока; l – вектор, равный по модулю длине l проводника и совпадающий по направлению с током; В – магнитная индукция поля.

Модуль вектора F определяется выражением

F = BIlsin

где α – угол между векторами I и В.

• Сила взаимодействия двух прямых бесконечно длинных параллельных проводников с токами I₁ и I₂, находящихся на расстоянии dдруг от друга, рассчитанная на отрезок проводника длиной lвыражается формулой

F = ₀I₁I₂l/2πd/

• Магнитный момент контура с током

p_m = IS

где S – вектор, равный по модулю площади S, охватываемой контуром, и совпадающий по направлению с нормалью к его плоскости.

• Механический момент, действующий на контур с током, помещённый в однородное магнитное поле,

M = [p_mB].

Модуль механического момента

M = p_mBsin,

где α – угол между векторами р_m и В.

Потенциальная (механическая) энергия контура с током в магнитном поле

П_мех= p_mB = p_mBcos α.

Сила, действующая на контур с током в магнитном поле (изменяющемся вдоль оси x),

F = p_m ∂B/∂х cos α,

где ∂B/∂х –изменение магнитной индукции вдоль оси Ох, рассчитанное на единицу длины; α – угол между векторами р_m и В.

Сила F, действующая на заряд Q, движущийся со скоростью v в магнитном поле с индукцией В (сила Лоренца), выражается формулой

F = Q [vB] или F = |Q|Bsin,

где – угол, образованный вектором скорости v движущейся частицы и вектором В индукции магнитного поля.
Примеры решения задач

Пример 4.1. По двум параллельным прямым проводам длиной l = 2,5 м каждый, находящимся на расстоянии d = 20см друг от друга, текут одинаковые токи

---

I = 1 кА.

1. Вычислить силу Fвзаимодействия токов.

2. Вычислить силу Fвзаимодействия, если токи уменьшились в два раза.

Решение. Взаимодействие двух проводников, по которым текут токи, осуществляется через магнитное поле. Каждый ток создаёт магнитное поле, которое действует на другой проводник. Предположим, что оба тока (обозначим их I₁и I₂) текут в одном направлении, снизу на верх.

Длинные проводники, длина которых длина много больше, чем расстояние между ними (l>>d), можно приближённо рассматривать как бесконечно длинные.

Вычислим силу F₁,₂, с которой магнитное поле, созданное током I₁, действует на проводник с током I₂. Для этого согласно правила буравчика проведём магнитную силовую линию так (штриховая окружность на рис. 4.1), чтобы она касалась проводника с током I₂. По касательной к силовой линии проведём вектор магнитной индукции В₁. Модуль магнитной индукции B₁ определяется соотношением


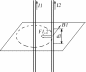Рис. 4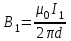.1
(1)

Согласно закону Ампера, на каждый элемент второго проводника длиной dl₂ с током I₂ действует в магнитном поле элемент силы 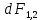, равный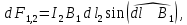



где 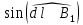– синус угла между элементом второго проводника с током I₂ и вектором магнитной индукции B₁.

Так как отрезок dl перпендикулярен вектору B₁, то 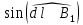равен единице, и выражение для определения элемента силы 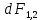примет вид

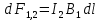. (2)

Направление элемента силы 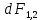рис. 4.1 определяется по правилу левой руки, то есть в ладонь входит магнитной индукции

---

B₁, четыре пальца показывают направление тока, а большой отогнутые палец покажет направление силы.

Подставив в формулу (2) выражение для вектора В₁из (1), получим



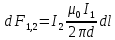
Силу F_1,2 взаимодействия проводников с током найдём интегрированием по всей длине второго проводника, при этом учтём, что токи равны I₁ = I₂ = I, длины проводников равны l₁ = l₂ = l, а также что направление силы F_1,2 совпадает с направлением элемента силы

F₁,₂ 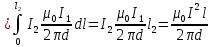(3)

Убедимся в том, что правая часть этого равенства дает единицу силы



Согласно третьему закону Ньютона, сила F_2,1, действующая на первый проводник со стороны второго, будет равна найденной (3) по модулю и противоположной по направлению.

1. Произведём вычисления по формуле (3) и получим окончательный результат:

.

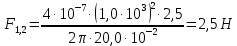2. Произведём вычисления по формуле (3) и получим окончательный результат в случае, когда токи уменьшились в два раза:

F_1,2 = 0,63 Н.



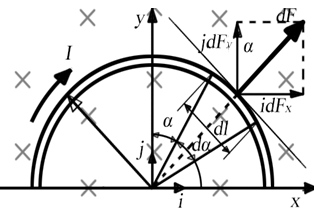
Рис. 4.2
Пример 4.2. Провод в виде тонкого полукольца радиусом R = 10 см расположен в плоскости чертежа (рис. 4.2) и находится в однородном магнитном поле, индукция B которого равна 50 мТл и . По проводу течёт ток I = 10 А. Найти силу F, действующую на провод, если плоскость полукольца перпендикулярна линиям магнитной индукции, которые направлены от нас, то есть в рисунок и обозначены крестиками, а подводящие провода находятся вне поля.

Решение. Выделим на полукольце малый элемент dl с током. На этот элемент тока Idlбудет действовать по закону Ампера сила dF = I[dlB]. Направление этой силы можно определить по правилу векторного произведения, то есть по правилу левой руки.

Для простоты вычислений используем симметрию, то есть выберем координатные оси так, как это изображено на рис. 4.2, то есть в центре полукольца. Силу

---

dF представим в виде



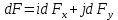
где i и j – единичные векторы (орты), требуемые теорией векторной алгебры, на вычисления они не как не влияют;

dF_xи dF_y — проекции вектора dF на координатные оси Ох и Оу.

Силу F, действующую на весь провод, найдём интегрированием:

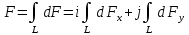, (1)

где символ Lуказывает на то, что интегрирование ведётся по всей длине провода L.

Из соображений симметрии, которую мы выбрали, первый интеграл (1) равен нулю, так как интеграл правой четверти полукольца имеет один знак, а интеграл левой четверти полукольца имеет другой знак, а сумма их равна нулю, так как их значения равны.

Тогда выражение (1) примет вид

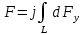⁽¹⁾

Из рис. 4.2 следует, что 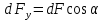, где dF – модуль вектора 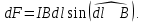Вектор dl перпендикулярен вектору В, значит .

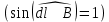Таким образом,

.

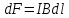Выразив длину дуги dl через радиус Rи угол α, получим



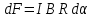
Тогда проекция вектора dF_у на координатную ось Оу равна



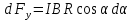
Введём dFyпод интеграл соотношения (1) и проинтегрируем в пределах от -π/2 до +π/2 (как это следует из рис. 4.2, где провод расположен в виде полуокружности):

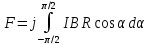. (2)

Из полученного выражения видно, что сила F сонаправлена с положительным направлением оси Оу (единичным вектором j).

Найдём модуль силы F, проинтегрировав выражение (2):



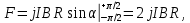
цифра 2 в результате появилась потому, что sin π/2 = 1, а sin π/2 = -1, их разность равна двум.

Убедимся в том, что правая часть этого равенства дает единицу силы (Н):

---