Добавлен: 18.10.2024
Просмотров: 25
Скачиваний: 0
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
СОДЕРЖАНИЕ
Определение реакций связей для двухопорной балки
Определение реакций связей для консольной балки
Определение траектории, скорости и ускорения точки по заданным уравнениям ее движения
Кинематический анализ механической системы при плоском движении
Применение теоремы об изменении кинетической энергии к изучению движения механической системы
на данном перемещении (рис. 5.6). Работа силы  является отрицательной и с учетом (5.17) в итоге определяется выражением
является отрицательной и с учетом (5.17) в итоге определяется выражением
Работа силы является положительной и с учетом (5.17) определяется выражением
является положительной и с учетом (5.17) определяется выражением
Работа пары сил является отрицательной и с учетом (5.17) определяется выражением
является отрицательной и с учетом (5.17) определяется выражением
Работа пары сил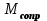 (момента трения качения) является отрицательной и с учетом (5.17), (5.33) определяется выражением
(момента трения качения) является отрицательной и с учетом (5.17), (5.33) определяется выражением
В итоге получаем, что сумма работ всех внешних сил, приложенных к телу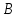 , определяется выражениями:
, определяется выражениями:
5.4.5. Работа внешних сил, действующих на механическую систему
Просуммируем работы внешних сил, действующих на тела механической системы. Для этого воспользуемся формулами (5.06), и Error: Reference source not found:
5.5. Расчет скоростей тел механической системы
В итоге мы получили, что кинетическая энергия всей системы согласно (5.0) определяется соотношением
Работа всех внешних сил согласно Error: Reference source not found равна
Согласно теореме об изменении кинетической энергии механической системы имеем равенство:
Подставим Error: Reference source not found и Error: Reference source not found в (5.45) и получим
Из Error: Reference source not found определяем
И в итоге находим скорость тела при прохождении им расстояния :
:
Воспользуемся соотношениями (5.0) и вычислим скорости всех тел данной механической системы:
5.6. Расчет ускорений тел механической системы
Мы получили формулу, связывающую функцию изменения перемещения тела от времени
от времени 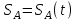 и функцию изменения скорости тела
и функцию изменения скорости тела  от времени
от времени 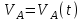 :
:
Продифференцируем левую и правую части уравнения Error: Reference source not found по времени и получим:
и получим:
Мы знаем, что производная от скорости является касательным ускорением, направленным вдоль траектории центра масс тела
является касательным ускорением, направленным вдоль траектории центра масс тела  :
:
Также мы знаем, что производная от перемещения является скоростью масс тела
является скоростью масс тела  :
:
Подставим (5.52) и Error: Reference source not found в (5.51) и получим:
Разделим обе части уравнения Error: Reference source not found на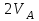 и получим выражение для вычисления ускорения тела
и получим выражение для вычисления ускорения тела  :
:
Зная ускорение по формулам, полученным при кинематическом анализе механической системы, рассчитаем ускорения всех тел системы
по формулам, полученным при кинематическом анализе механической системы, рассчитаем ускорения всех тел системы
Направления рассчитанных ускорений показаны на рис. 5.7.
6.6. Расчет натяжения нитей на всех участках
Из выражения (5.18) определим натяжение нити на первом участке
Зная ускорение по формулам (5.19) и (5.22), рассчитаем значение силы натяжения нити (троса) на первом участке по (5.57)
по формулам (5.19) и (5.22), рассчитаем значение силы натяжения нити (троса) на первом участке по (5.57)
Из выражения (5.28а) определим натяжение нити на втором участке
Зная ускорение по формуле (5.58), рассчитаем значение силы натяжения нити (троса) на втором участке по (5.59)
по формуле (5.58), рассчитаем значение силы натяжения нити (троса) на втором участке по (5.59)
6.7. Расчет силы трения, приложенной в точке касания колеса В с плоскостью
Из выражения (5.36) определим силу трения, приложенной в точке касания колеса В с плоскостью
Зная значения всех величин входящих в формулу (5.61), определим значение этой силы
 является отрицательной и с учетом (5.17) в итоге определяется выражением
является отрицательной и с учетом (5.17) в итоге определяется выражением 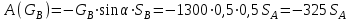 . . | (5.37) |
Работа силы
 является положительной и с учетом (5.17) определяется выражением
является положительной и с учетом (5.17) определяется выражением 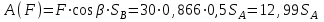 . . | (5.38) |
Работа пары сил
 является отрицательной и с учетом (5.17) определяется выражением
является отрицательной и с учетом (5.17) определяется выражением 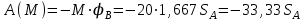 , , | (5.39) |
Работа пары сил
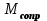 (момента трения качения) является отрицательной и с учетом (5.17), (5.33) определяется выражением
(момента трения качения) является отрицательной и с учетом (5.17), (5.33) определяется выражением 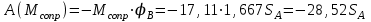 , , | (5.40) |
В итоге получаем, что сумма работ всех внешних сил, приложенных к телу
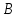 , определяется выражениями:
, определяется выражениями: 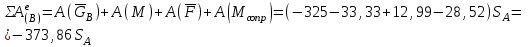 . . | (5.41) |
5.4.5. Работа внешних сил, действующих на механическую систему
Просуммируем работы внешних сил, действующих на тела механической системы. Для этого воспользуемся формулами (5.06), и Error: Reference source not found:
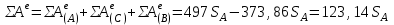 . . | (5.42) |
5.5. Расчет скоростей тел механической системы
В итоге мы получили, что кинетическая энергия всей системы согласно (5.0) определяется соотношением
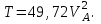 | (5.43) |
Работа всех внешних сил согласно Error: Reference source not found равна
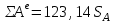 . . | (5.44) |
Согласно теореме об изменении кинетической энергии механической системы имеем равенство:
 . . | (5.45) |
Подставим Error: Reference source not found и Error: Reference source not found в (5.45) и получим
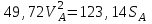 . . | (5.46) |
Из Error: Reference source not found определяем
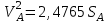 . . | (5.47) |
И в итоге находим скорость тела при прохождении им расстояния
 :
: 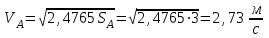 . . | (5.08) |
Воспользуемся соотношениями (5.0) и вычислим скорости всех тел данной механической системы:
 | (5.49) |
5.6. Расчет ускорений тел механической системы
Мы получили формулу, связывающую функцию изменения перемещения тела
 от времени
от времени 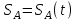 и функцию изменения скорости тела
и функцию изменения скорости тела  от времени
от времени 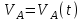 :
: 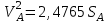 . . | (5.50) |
Продифференцируем левую и правую части уравнения Error: Reference source not found по времени
 и получим:
и получим: 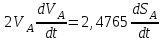 . . | (5.51) |
Мы знаем, что производная от скорости
 является касательным ускорением, направленным вдоль траектории центра масс тела
является касательным ускорением, направленным вдоль траектории центра масс тела  :
: 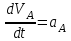 . . | (5.52) |
Также мы знаем, что производная от перемещения
 является скоростью масс тела
является скоростью масс тела  :
:  . . | (5.53) |
Подставим (5.52) и Error: Reference source not found в (5.51) и получим:
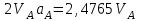 . . | (5.54) |
Разделим обе части уравнения Error: Reference source not found на
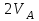 и получим выражение для вычисления ускорения тела
и получим выражение для вычисления ускорения тела  :
:  . . | (5.55) |
Зная ускорение
 по формулам, полученным при кинематическом анализе механической системы, рассчитаем ускорения всех тел системы
по формулам, полученным при кинематическом анализе механической системы, рассчитаем ускорения всех тел системы 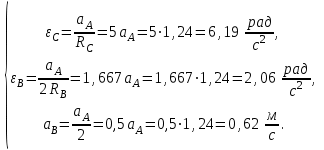 | (5.56) |
Направления рассчитанных ускорений показаны на рис. 5.7.
 |
| Рис. 5.7. Ускорения тел механической системы |
6.6. Расчет натяжения нитей на всех участках
Из выражения (5.18) определим натяжение нити на первом участке
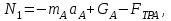 | (5.57) |
Зная ускорение
 по формулам (5.19) и (5.22), рассчитаем значение силы натяжения нити (троса) на первом участке по (5.57)
по формулам (5.19) и (5.22), рассчитаем значение силы натяжения нити (троса) на первом участке по (5.57) 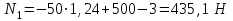 | (5.58) |
Из выражения (5.28а) определим натяжение нити на втором участке
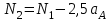 | (5.59) |
Зная ускорение
 по формуле (5.58), рассчитаем значение силы натяжения нити (троса) на втором участке по (5.59)
по формуле (5.58), рассчитаем значение силы натяжения нити (троса) на втором участке по (5.59) 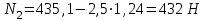 | (5.60) |
6.7. Расчет силы трения, приложенной в точке касания колеса В с плоскостью
Из выражения (5.36) определим силу трения, приложенной в точке касания колеса В с плоскостью
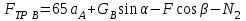 , , | (5.61) |
Зная значения всех величин входящих в формулу (5.61), определим значение этой силы
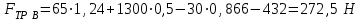 , , | (5.62) |
