Добавлен: 18.10.2024
Просмотров: 24
Скачиваний: 0
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
СОДЕРЖАНИЕ
Определение реакций связей для двухопорной балки
Определение реакций связей для консольной балки
Определение траектории, скорости и ускорения точки по заданным уравнениям ее движения
Кинематический анализ механической системы при плоском движении
Применение теоремы об изменении кинетической энергии к изучению движения механической системы
Задача 2.
Определение реакций связей для консольной балки
2.1. Задание на расчет
Определить реакции наложенных на балку внешних связей. Форма и размеры балки с приложенными к ней внешними нагрузками представлены на рис. 2.1.
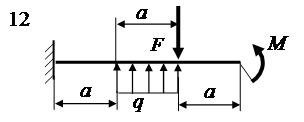
Рис. 2.1. Прямая балка, ее размеры, наложенные на нее связи и действующие на нее нагрузки
Исходные данные
Задана прямая балка, нагруженная силой
 , парой сил с моментом
, парой сил с моментом  и равномерно распределенной нагрузкой интенсивностью
и равномерно распределенной нагрузкой интенсивностью  (рис. 2.2). Балка жестко закреплена на левом конце (заделка в точке
(рис. 2.2). Балка жестко закреплена на левом конце (заделка в точке  ). Размеры балки показаны на рис. 2.2.
). Размеры балки показаны на рис. 2.2.Расчеты выполнить при исходных данных, заданных в табл. 2.1
Таблица 2.1
 |  |  |  |
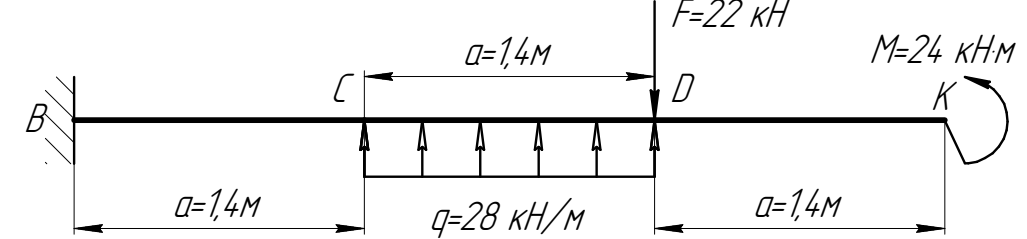
Рис. 2.2. Прямая балка, ее размеры, наложенные на нее связи и действующие на нее нагрузки (числовые данные)
2.2. Определение реакций внешних связей
Для определения опорных реакций (реакций наложенных на балку внешних связей), изобразим в масштабе на рис. 2.3 соответствующую расчетную схему и выполним следующие необходимые действия.
1. Для исключения ошибок, связанных с размерностями рассматриваемых в расчетах величин, необходимо согласно системе СИ:
-
размеры измерять в метрах ( );
); -
силы измерять в ньютонах ( );
); -
моменты пар сил измерять в ньютон - метрах ( );
); -
интенсивности распределенной нагрузки измерять в ньютонах, приходящихся на один метр ( ).
).
В итоге запишем:
 | (2.0) |
2. Изобразим балку и связанные с ней оси
 правой декартовой системы координат
правой декартовой системы координат  (рис. 2.3).
(рис. 2.3).3. Заменим равномерно распределенную нагрузку
 , действующую на участке
, действующую на участке  , ее равнодействующей
, ее равнодействующей  , модуль которой определяется как площадь фигуры (прямоугольника), изображающей на рис. 2.2 распределённую нагрузку
, модуль которой определяется как площадь фигуры (прямоугольника), изображающей на рис. 2.2 распределённую нагрузку  :
:  . . | (2.0) |
Сила
 направляется в ту же сторону, что и распределенные силы
направляется в ту же сторону, что и распределенные силы  , а линия действия силы
, а линия действия силы  проходит через центр тяжести фигуры (прямоугольника), изображающей распределённую нагрузку
проходит через центр тяжести фигуры (прямоугольника), изображающей распределённую нагрузку  . В итоге на рис. 2.3 показана сила
. В итоге на рис. 2.3 показана сила  , заменяющая распределенную нагрузку
, заменяющая распределенную нагрузку  , и задано расстояние (
, и задано расстояние ( ) от точки
) от точки  до линии действия силы
до линии действия силы 
.
4. Приложим к балке все внешние задаваемые силы
 (рис. 2.3).
(рис. 2.3).5. Согласно принципу освобождаемости тел от связей отбросим мысленно внешние связи (заделку в сечении
 на рис. 2.2) и заменим их соответствующими реакциями связей (рис. 2.3).
на рис. 2.2) и заменим их соответствующими реакциями связей (рис. 2.3).В точке
 имеем три связи действие которых заключается в создании трех реакций связей (рис. 2.3).:
имеем три связи действие которых заключается в создании трех реакций связей (рис. 2.3).:-
силы-реакции , направленной вдоль оси
, направленной вдоль оси  ;
; -
силы-реакции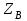 , направленной вдоль оси
, направленной вдоль оси  ;
; -
момента заделки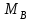 .
.
На расчетной схеме силы-реакции
 ,
, 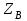 направляем в сторону направления соответствующих координатных осей
направляем в сторону направления соответствующих координатных осей  , а момент заделки
, а момент заделки 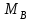 в направлении противоположном вращению часовой стрелки (рис. 2.3).
в направлении противоположном вращению часовой стрелки (рис. 2.3).Таким образом, нам необходимо определить три неизвестных реакций связей
(
 ):
):  ,
, 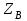 ,
, 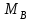 (рис. 2.3).
(рис. 2.3). 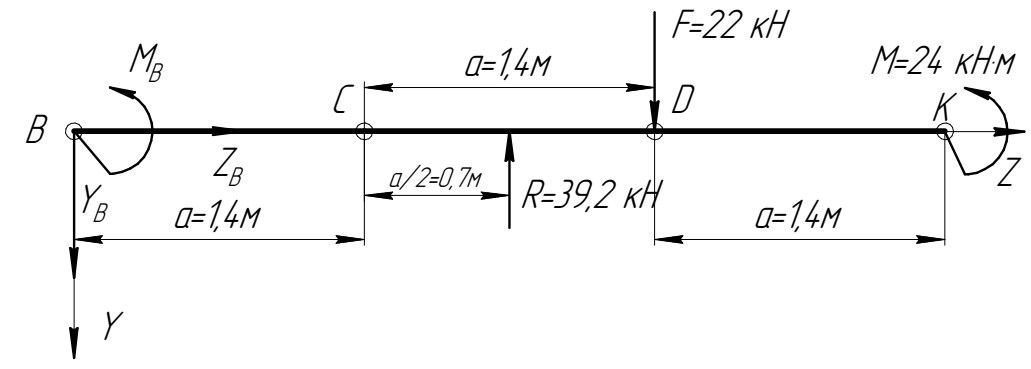 |
| Рис. 2.3. Расчетная схема балки при определении опорных реакций |
6. Записываем для изображенной на рис. 2.3 плоской системы сил три уравнения равновесия (
 ):
): 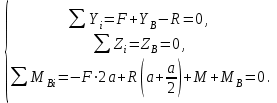 | (2.0) |
Число уравнений равновесия в системе (1.0) равно числу неизвестных реакций
(
 ). Из этого следует, что все неизвестные реакции можно определить из уравнений равновесия. В этом случае говорят, что балка статически определима.
). Из этого следует, что все неизвестные реакции можно определить из уравнений равновесия. В этом случае говорят, что балка статически определима.Подставим в систему уравнений (1.0) заданные силы, момент пары сил и заданные размеры и после ряда преобразований и вычислений получим:
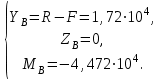 | (2.0) |
Знак минус у значения момента пары сил
 указывает на то, что действительное направление пары сил
указывает на то, что действительное направление пары сил  противоположно их изображениям на рис. 2.3.
противоположно их изображениям на рис. 2.3.7. Для проверки правильности расчетов запишем уравнение равновесия моментов относительно любой другой точки, за исключением ранее использованной точки
 .
.Но перед этим необходимо изменить направление всех тех реакций связей, значения которых получились отрицательными и заново изобразить полученную расчетную схему на рис. 2.4.
В рассматриваемом случае меняем направления пары сил
 . В итоге реакции всех связей становятся положительными и далее при работе с рис. 2.4 мы используем значения:
. В итоге реакции всех связей становятся положительными и далее при работе с рис. 2.4 мы используем значения: 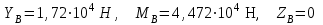 . . | (2.0) |
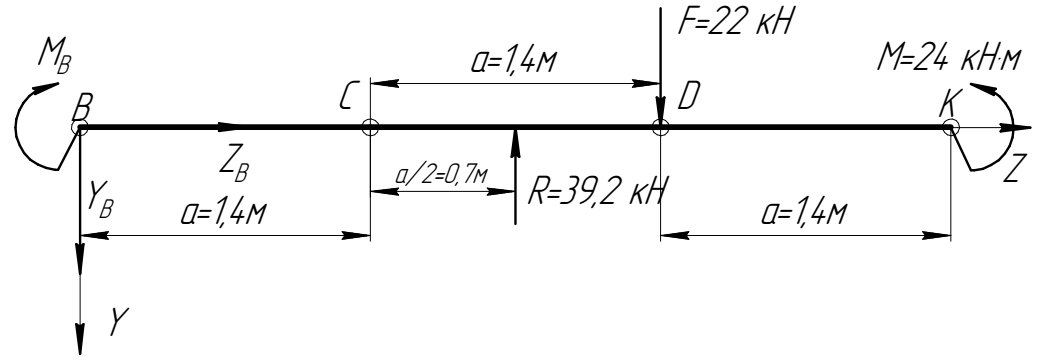 |
| Рис. 2.4. Измененная расчетная схема балки при положительных значениях реакций связей для проверки точности их расчетов |
Затем на рис. 2.4 выберем за полюс какую-либо точку (например, точку
 ) и проверим, как в этом случае соблюдается уравнение равновесия моментов при значениях реакций связей, выбираемых из Error: Reference source not found:
) и проверим, как в этом случае соблюдается уравнение равновесия моментов при значениях реакций связей, выбираемых из Error: Reference source not found:
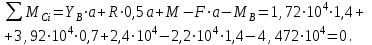 | (2.6) |
Равенство нулю суммы моментов всех сил относительно точки
 подтверждает правильность найденных значений реакций связей
подтверждает правильность найденных значений реакций связей  ,
,  ,
,  .
.