Добавлен: 18.10.2024
Просмотров: 27
Скачиваний: 0
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
СОДЕРЖАНИЕ
Определение реакций связей для двухопорной балки
Определение реакций связей для консольной балки
Определение траектории, скорости и ускорения точки по заданным уравнениям ее движения
Кинематический анализ механической системы при плоском движении
Применение теоремы об изменении кинетической энергии к изучению движения механической системы
Задача 3.
Определение траектории, скорости и ускорения точки по заданным уравнениям ее движения
3.1. Задание на расчет
По заданным уравнениям движения точки М установить вид её траектории и для момента времени
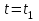 (с) найти положение точки на траектории, её скорость, полное, касательное и нормальное ускорения, а также радиус кривизны траектории.
(с) найти положение точки на траектории, её скорость, полное, касательное и нормальное ускорения, а также радиус кривизны траектории.Необходимые для решения данные приведены в табл. 20.
Таблица 20
| Уравнения движения | 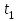 , с , с | |
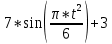 . .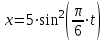 | 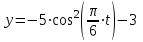 | 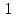 |
Решение:
Параметрические уравнения движения точки имеют вид:
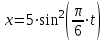 , , 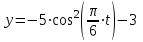 | (3.1) |
Уравнение траектории. Для определения уравнения траектории точки исключим время
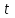 из заданных уравнений движения.
из заданных уравнений движения.Для определения уравнения траектории, из уравнения
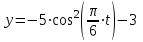 находим,
находим,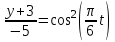
из уравнения
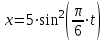 находим,
находим,
Преобразованные уравнения почленно сложим. Тогда
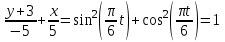 | (3.2) |
получаем уравнение траектории из уравнения (3.2)
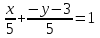 | (3.3) |
или
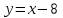 | (3.4) |
Из уравнения (3.4) следует, что траекторией точки является прямая линия. (рис.3.1).
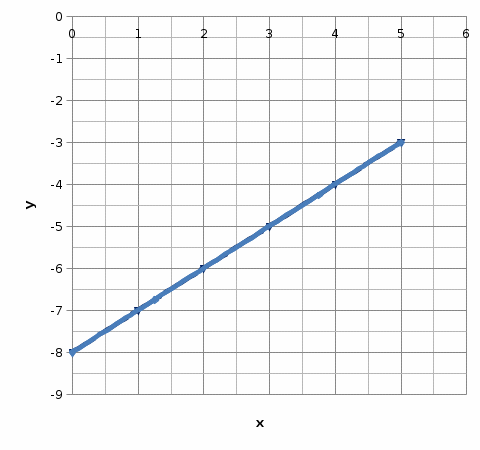 |
| Рис. 3.1. Траектория точки заданная уравнениями (3.1) в параметрической форме и уравнением (3.4) в координатной форме |
Координаты точки в начальный момент движения равны:
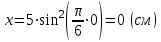 , , 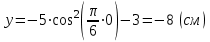 | (3.5) |
Координаты точки в момент времени
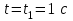 равны:
равны: 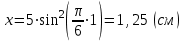 , , 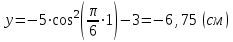 | (3.6) |
Вектор скорости точки
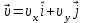 , , | (3.7) |
Вектор ускорения
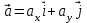 , , | (3.8) |
Здесь
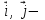 орты осей х и у;
орты осей х и у; 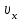 ,
, 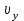 ,
, 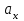 ,
, 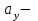 проекции скорости и ускорения точки на оси координат.
проекции скорости и ускорения точки на оси координат.Законы изменения проекций скорости и ускорения точки во времени
получаем дифференцированием выражений (3.1):
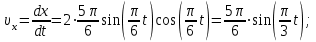 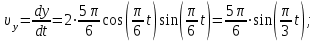 | (3.9) |
По найденным проекциям определяется модуль скорости
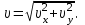 | (3.10) |
Значение проекций и модуля скорости при t1 = 1 c, см/с:
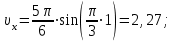 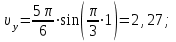 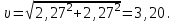 | (3.11) |
Аналогично найдем ускорение точки:
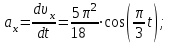 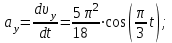 | (3.12) |
По найденным проекциям определяется модуль скорости
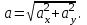 | (3.13) |
Значение проекций и модуля ускорения при t1 = 1 c, см/с2:
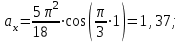 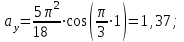 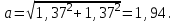 | (3.14) |
Касательное ускорение найдем, дифференцируя по времени равенство
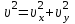 . Получим:
. Получим: 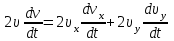 | (3.15) |
Из уравнения (3.15)
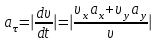 | (3.16) |
Числовые значения всех величин, входящих в правую часть выражения (3.16), определены и даются равенствами (3.11) и (3.14). Подставив в (3.16) эти числа, найдем сразу, что при t1 =1 с,
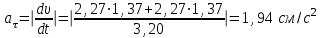 | (3.17) |
Нормальное ускорение точки:
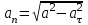 . Подставляя сюда найденные числовые значения а, и аτ получим, что при t1= 1 c ,
. Подставляя сюда найденные числовые значения а, и аτ получим, что при t1= 1 c , 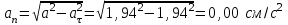 | (3.18) |
Радиус кривизны траектории:
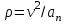 | (3.19) |
Подставляя в (3.19) числовые значения vи ап, найдем, что при t1 = 1 с
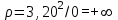 | (3.20) |
Результаты вычислений для заданного момента времени t1 1 с приведены в таблице 3.1.
Таблица 3.1
| Координаты, см | Скорость, см/с | Ускорение, см/с2 | Радиус кривизны, м | |||||||
| x | y | vх | vу | v | aх | aу | a | aτ | aп | |
| 1,25 | -6,75 | 2,27 | 2,27 | 3,20 | 1,37 | 1,37 | 1,94 | 1,94 | 0,0 |  |
На рис.3.2 показано положение точки
М в заданный момент времени. Вектор
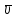 строим по составляющим
строим по составляющим 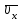 и
и 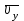 , причем этот вектор должен по направлению совпадать с касательной по траектории. Вектор
, причем этот вектор должен по направлению совпадать с касательной по траектории. Вектор 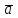 строим по составляющим
строим по составляющим 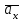 и
и 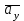 , и затем раскладываем на составляющие
, и затем раскладываем на составляющие 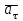 и
и 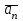 . Совпадение величин
. Совпадение величин 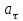 и
и 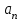 , найденных из чертежа, с их значениями, полученными аналитически, служит контролем правильности решения
, найденных из чертежа, с их значениями, полученными аналитически, служит контролем правильности решения 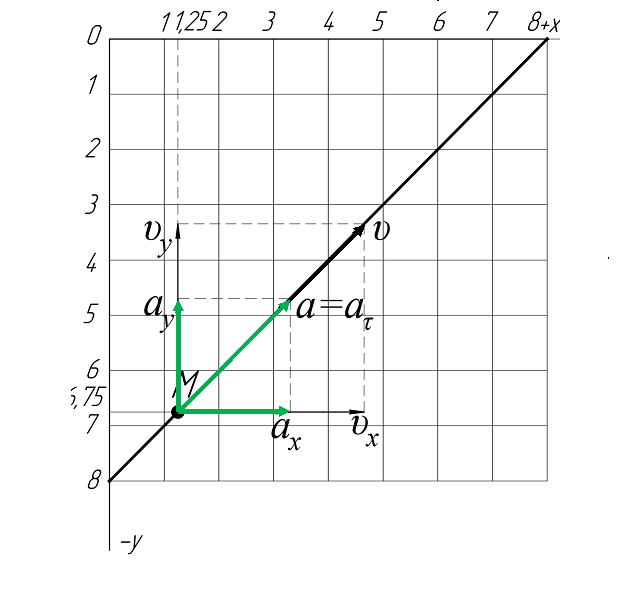 |
| Рис. 3.2. Положение точки М в заданный момент времени |
